高速铁路大跨度连续刚构梁桥预拱度设置对无砟轨道的影响研究

王安琪,姜恒昌,张光明,杨荣山,褚卫松

(西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)

引言

随着高速铁路在全国范围内的大规模推进，大跨度混凝土梁桥被广泛应用，在大跨度桥上铺设无砟轨道已成为高速铁路工程结构建设的关键技术之一[1-2]。目前，日本等国家的高速铁路桥梁采用无砟轨道已比较普遍[3]，但多以中小跨度桥梁为主，100 m以上的大跨度桥梁应用较少，高铁大跨桥上速度目标值与线路保持一致，增加了大跨度桥梁设计建造及施工工艺的难度，国内有关实践经验较少，相关技术还不成熟。

以往关于无砟轨道在高速铁路大跨度桥梁上的研究主要集中在解决梁体刚度和变形控制技术上，文献[4]通过分析梁体基频、刚度和变形设计值与实测值的差异成因，对高速铁路常用跨度简支箱梁进行优化设计；文献[5-6]针对梁体基频、竖向刚度、梁结构刚度、梁端转角等关键技术，结合我国高速铁路桥梁参数的研究思路、参数设计及运营现状，采用车桥竖向相互作用程序分析了高铁简支梁动力响应规律；文献[7-8]从大跨混凝土桥梁的徐变系数、铺装时间等方面出发，对桥梁徐变上拱、下挠的控制进行分析，提出大跨度无砟轨道桥梁建设时减小徐变变形的措施和方法。

上述文献的研究对象都集中在桥梁结构本身，通过对桥梁各关键参数及变形控制技术的分析，探究桥梁结构能够满足无砟轨道铺设的要求。而针对桥梁线形变化对轨道结构影响的研究相对较少，桥梁结构的线形变化十分复杂，影响因素很多，主要通过设置预拱度[9]的方法加以控制，预拱度设置的合理与否直接影响桥梁线形的优劣。目前国内的大跨度混凝土连续梁桥普遍存在着跨中下挠过大的问题[10]，使得桥梁线形不符合高速铁路无砟轨道的高平顺要求[11]，进而影响轨道的几何形位、危及行车安全。

为此，根据某连续刚构梁桥工程实际参数，建立桥梁整体有限元模型，利用经验公式为桥梁设置预拱度，计算分析无砟轨道铺设过程中预拱度的设置对桥梁线形的影响，得出桥梁线形及其对轨道波长不平顺影响的变化规律，为后续大跨度连续刚构桥梁上铺设无砟轨道提供相关计算参考。

1 工程背景

本文所依托的大跨度连续刚构梁桥位于陕西省铜川市王益区境内，桥跨径组合为(124+248+124) m连续刚构加拱梁桥，主梁为预应力混凝土结构，采用单箱双室变高度箱形截面，箱梁顶宽14 m，底宽10.6 m，下部主墩为矩形空心结构，纵、横向均为直坡，纵向宽9.0 m，横向宽13.1 m，壁厚1.5 m。全桥除梁拱结合部在支架上施工外，其余梁段均采用挂篮悬臂浇筑。主桥立面如图1所示。

图1 连续刚构梁桥主桥立面示意(单位：cm)

2 预拱度设置

根据连续刚构桥结构变形的性质和时间不同，预拱度可分为施工预拱度和成桥预拱度[12]。施工预拱度的设置主要是为了消除施工过程中各种荷载和变形(包括桥梁自重、二期恒载、温度、混凝土前期收缩徐变等)对成桥线形的影响，成桥预拱度的设置则是为了消除运营过程中后期收缩、徐变、活载变形等对桥面线形的影响。理想状态下，桥梁的成桥线形(即桥梁施工完毕后的线形)为设计线形加成桥预拱度的线形；最终线形(即桥梁运营过程中收缩徐变基本完成时的线形)与设计线形基本一致。

根据目前国内的经验，常用的成桥预拱度设置方法一般有二次抛物线分配法和余弦分配法[13-14]。为了避免二次抛物线分配法在桥墩顶处出现尖点导致成桥线形不平顺、不协调的问题，本文采用余弦分配法对连续刚构梁桥的成桥预拱度进行设置。

中跨成桥预拱度曲线方程为

边跨一般根据经验在3L/8处设置fcz/4左右的预拱度，分配方式同样采用余弦曲线，边跨成桥预拱度余弦曲线方程为

式中，L为中跨跨径；fcz为中跨跨中成桥预拱度。

根据近几年的实践，跨中最大预拱度一般取L/1 500～L/1 000，本文所选用的连续刚构梁桥中跨长为248 m，根据实际情况将预拱度设置精度精确到10 mm，故预拱度值取值区间为[0.170 m，0.250 m]，预拱度梯度取值0.02 m，最终可确定0.170，0.190，0.210，0.230，0.250 m作为5个预拱度的取值。

3 模型的建立与分析

为探究不同工况下无砟轨道铺设引起的桥梁线形及其对轨道结构几何形位影响的变化规律，以CRTSⅠ型双块式无砟轨道为研究对象，利用有限元法建立完整的连续刚构桥梁模型，依据施工图设计文件确定模型各部分尺寸。其中，梁顶板、底板、腹板、桥墩中部采用Shell181单元模拟，桥墩顶部、底部采用Solid65单元模拟，横撑采用Beam188单元模拟、吊杆采用Link10单元模拟，拱肋通过梁板组合单元模拟，根据确定的单元类型和模型尺寸建立连续刚构桥有限元模型如图2所示。

图2 连续刚构桥有限元模型

结合现场实际给模型施加恒载+温度效应的荷载组合，具体计算时，有如下假定：

(1)忽略轨道结构与桥梁之间的相对位移，认为无砟轨道结构依附于梁体表面随梁体共同变形，桥面节点位置根据预先设置的预拱度曲线确定；

(2)轨道结构作为均布荷载施加于桥面上，计算时以7.5 m为一个荷载周期，沿线路方向逐步施加均布荷载；

(3)根据叠加原理，不同轨道施工顺序所造成的桥面最终下沉量是一致的，故不考虑无砟轨道铺设顺序对桥梁下沉量的影响，仅根据施工的经济性以及易操作性对模型施加均布荷载。

根据建立的模型及相关计算假定，得到5种工况下桥的最终成桥线形如图3所示。

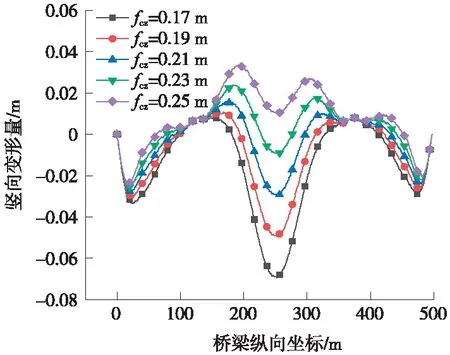
图3 不同预拱度下桥梁成桥线形

从图3可以看出，桥梁在荷载作用下呈现对称式的变形，中跨跨中下沉量最大，边跨总体下沉量小且最大下沉值出现在距离边跨端点3L/8处左右，与之前成桥预拱度的设置中边跨、中跨的最大下沉位置相符。

5种不同预拱工况下桥梁最终成桥线形产生很大变化，随着预拱度设置的增大，桥梁线形由整体下挠逐渐转变为上拱。预拱度设置为0.17 m时，桥梁整体线形几乎完全下挠于水平线以下，跨中处有最大下挠值45 mm；预拱度设置为0.25 m时，桥梁中跨的成桥线形则完全上拱于水平线上，支座处有最大上拱值46 mm；其他预拱工况下桥梁线形的波形变化趋势相同而幅值介于两者之间。

可以看出，当桥梁预拱度设置过小时，轨道二期恒载引起的桥梁结构变形不足以被预设拱度所抵消，荷载作用下桥梁仍有很大程度的下挠，当预拱度设置过大时，过大的预拱值又会使桥梁支座处产生较大的上拱，这两者对于桥上轨道的几何状态来说都是不利的，甚至会危及行车安全。

4 桥梁线形对轨道结构高低平顺性的影响

为进一步探究桥梁线形对轨道结构高低不平顺的具体影响，根据弦测法对轨道的高低不平顺变化规律进行研究。线路的高低不平顺采用弦测法[15-16]计算，30 m弦每隔5 m校核值不应超过2 mm，300 m弦每隔150 m校核值不应超过10 mm。具体高低不平顺矢度计算方法如下。

30 m(48个轨枕间距)弦线按间距5 m(8个轨枕间距)设置1对检测点，见图4。图4中C1～C49为30 m范围内轨枕编号，h2～h48分别为30 m弦范围内C2～C48轨枕处矢高。以C25与C33轨枕为例，中波不平顺校核值通过两点间实际矢高差与设计矢高差差值控制，按照公式(1)计算。

Δh=|(h25设计-h33设计)-(h25实测-h33实测)|

(1)

图4 30 m弦中波不平顺检测

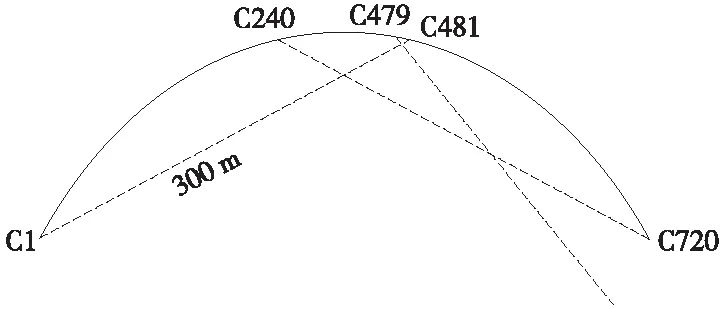
图5 300 m弦长波不平顺检测示意

300 m(480个轨枕间距)弦线每150 m(240个轨枕间距)设置1对检测点，见图5。图5中C1～C481为300 m范围内轨枕编号，h2～h480分别为C2～C480轨枕处矢高。以C25与C265为例，长波不平顺校核值通过两点间实际矢高差与设计矢高差差值控制，按照公式(2)计算。

Δh=|(h25设计-h265设计)-(h25实测-h265实测)|

(2)

根据上述弦测计算法，得到轨道结构各波长高低不平顺值与桥梁长度之间的关系如图6～图7所示。

图6 不同预拱度下30 m/5 m校核值

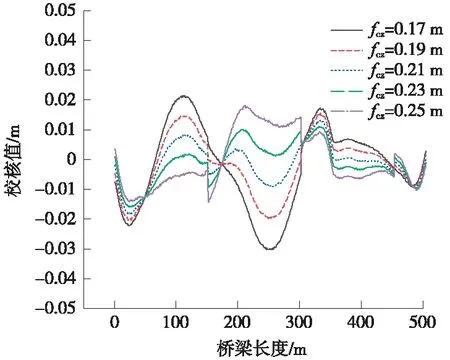
图7 不同预拱度下300 m/50 m校核值

从图6、图7可以看出，5种工况下的桥梁线形引起的轨道结构30 m弦隔5 m校核值均小于规范所规定的2 mm限值，而300 m弦每隔150 m校核值在某些工况下已远超出规范规定的10 mm限值，即不同预拱度下轨道结构的中波不平顺均满足要求，而长波不平顺则有很大差异，可见预拱度的设置及轨道二期恒载主要对轨道结构的长波不平顺产生影响。

从图7的计算结果可以看出，5种工况下轨道结构的长波不平顺波形变化大致相同而幅值不同，当预拱度设置在0.21～0.23 m时，轨道结构的长波不平顺校核值基本没有超过规定限值，但当预拱度设置大于0.23 m，或小于0.21 m时，轨道的长波不平顺校核值则已明显超限，可见预拱度设置的过大或过小，都会使桥梁线形形成的轨道长波高低不平顺不满足规范要求。

5 结论

针对轨道铺设过程中大跨度连续刚构梁桥预拱度设置对桥梁线形及轨道高低不平顺影响的问题，利用ANSYS有限元分析软件，建立桥梁结构整体模型进行计算分析，得到如下结论。

(1)在大跨度桥梁上铺设无砟轨道时，轨道二期恒载与预拱度设置会引起桥梁最终成桥线形的变化，预拱度设置的合理与否直接影响桥梁成桥线形的优劣，从而导致轨道结构的高低平顺性发生变化，且长波高低不平顺的影响最为显著。

(2)在高速铁路大跨度桥梁上铺设对线形要求高的无砟轨道时，需要关注桥梁线形对轨道结构的影响，建议在桥梁设计施工阶段，建立完整的桥梁结构模型，综合考虑影响线形的各因素，并对桥梁最终线形造成的轨道长波高低不平顺值进行检算，以满足规范规定的限值要求。