考虑政府补贴和风险规避的绿色供应链决策模型

梁晓蓓， 江 江， 孟 虎， 杨以雄

(1.同济大学 经济与管理学院，上海200092;2.东华大学 服装与艺术设计学院，上海200051)

1 引言

随着经济快速发展，自然资源过度消耗等问题逐渐凸显，世界各国和地区都在寻找环境影响最小化的绿色发展模式［1～3］。一些企业已经开始了基于绿色技术的差异化之路，并取得了良好的声誉和收益［4～6］。然而，现阶段性价比低、消费者环保意识弱等情况通常会导致绿色产品的实际需求低于预测量［2，3，7～10］，使得供应链成员面临着较大风险，其积极性也被明显挫伤。迹象表明，在绿色供应链发展前期，政府补贴不能“缺位”［1］。此外，在风险较大的绿色供应链中，供应链成员的风险态度也会对供应链管理绩效产生重要影响。如何在考虑供应链成员风险规避特性的基础上有效地设计政府补贴策略和绿色供应链管理策略，是现阶段需要解决的重要问题。

已有学者研究了绿色供应链中的政企博弈问题，主要包括两类:一是将政府补贴作为博弈模型中的参数，分析补贴模式对绿色供应链决策的影响。Mitra 和Webster［11］分析了政府补贴再制造商、制造商或同时补贴二者三种政府补贴模式的影响。朱庆华等［1］分析了无补贴、补贴制造商或消费者三种模式对决策及成员收益的影响。张艳丽等［2］在朱庆华等［1］的基础上，进一步考量了消费者策略行为。温兴琦等［3］分析了以制造商为补贴对象的绿色度(即企业全部的生产经营活动的环境友好程度)补贴、生产或研发成本补贴三种策略的影响。研究发现，补贴生产商时，政府补贴增加有助于降低价格和增加市场份额［1，2］;补贴消费者时，绿色产品批发价格会随着政府补贴系数的增加而增加［1，2］;研发成本补贴策略对产品绿色度提升最具效度，生产成本补贴策略最受制造商青睐，而零售商更倾向于绿色度补贴策略［3］。无论何种模式，政府补贴都有助于增加绿色产品生厂商及供应链系统利润［1，2，11］。二是将政府补贴作为博弈模型中的决策变量，分析政府及供应链的最优决策及不同补贴模式对绿色供应链决策的影响。朱庆华和窦一杰［7］分析了绿色度补贴模式下制造商的最优产品绿色度及政府的最优补贴系数。孙迪和余玉苗［8］在朱庆华和窦一杰［7］的基础上，进一步研究发现，绿色度补贴模式下政府补贴系数提升有助于降低绿色产品价格［8］;消费者补贴模式下产品价格会随着政府补贴系数的提升而上升［8］;无论哪种补贴模式，政府补贴都有助于促进生产商利润和整体社会福利提高［8］。

而考虑决策者风险规避特性的绿色供应链管理研究文献相对较少。Cao 等［12］分析了一个风险中性的制造商和N 个风险规避的分销商之间的博弈模型，探究了分销商数量、风险规避度及市场需求的不确定性对绿色产品定价、订货量及供应链成员收益的影响，研究发现:分销商风险规避度的提升，对批发价格并不产生影响，但会降低零售价格，致使制造商和供应链系统期望效用下降。江世英和马春艳［10］构建了一个风险中性制造商与风险规避零售商组成的二级绿色供应链博弈模型，探讨了零售商风险规避度、产品绿色度及产品定价之间的相互影响。随后，江世英等［9］进一步考虑了制造商的风险规避特性。研究发现，集中决策模式下，制造商风险中性情境中风险规避的零售商将无利可图［10］;分散式决策模式下，零售商风险规避度提升会促进产品价格下降［10］，产品批发和零售价格在制造商风险中性、零售商风险规避时最高，制造商风险规避、零售商风险中性时最低［9］。

综上可知，政企博弈视角的绿色供应链研究相对成熟，考虑成员风险规避特性的相关研究虽偏少，但已逐渐被学术界重视。然而，目前尚缺乏综合考虑政企博弈和成员风险规避特性的绿色供应链管理研究。本文通过构建政府与一个制造商和零售商组成的二级绿色供应链间的博弈模型，研究制造商和零售商分散和集中决策两种模式下、四种不同风险规避情境中政府及供应链成员的最优决策、期望效用和社会福利，通过数值推理和仿真，分析政府补贴和供应链成员的风险规避特性对供应链最优决策及收益和社会福利等方面的影响，以期为政府及绿色供应链成员提供决策参考。

2 模型描述与基本假设

本文建立了政府与由一个制造商和零售商组成的二级绿色供应链间的三阶段和两阶段博弈模型［11］。三阶段博弈模型中制造商和零售商分散决策，第一阶段是政府依据期望社会福利最大化确定对制造商的补贴比例γ;第二阶段是制造商决定产品绿色度g 和批发价格ω，实际操作中，产品绿色度通过有害物质含量、碳标签、可回收程度等显现;第三阶段是零售商以零售价格p 进行市场销售(p ＞ω)。两阶段博弈模型中制造商和零售商集中决策，第一阶段是政府确定补贴比例;第二阶段是制造商和零售商确定产品绿色度和价格。出于研究需要，本文做以下假设:

(1)市场需求随产品零售价格p 单调递减，随产品绿色度g 单调递增［3，5，13］，且市场需求存在不确定性［9］。需求函数为D=a －bp +kg +ε，其中a 表示市场潜在需求，b、k 分别表示市场需求对产品零售价格和绿色度的敏感系数(b，k ＞0)，且a ＞bp［3］，ε表示市场需求的不确定性，ε 服从均值为0、方差为σ2的正态分布，即ε∈N(0，σ2)［9］。

(2)假设不考虑制造商的生产成本和零售商的固定和销售成本［14］。制造商前期投入的产品绿色化研发成本cd与产品绿色度成二次方关系［1，5，14～17］，即cd=zg2/2［3，9］，研发投入是全部由制造商承担的一次性投入，其中z 为研发投入成本系数［3］，是一个较大的正常量［5］。

(3)为激励制造商加大绿色投入，政府按照研发成本的一定比例γ ∈(0，1)对制造商进行补贴［3］。

(4)ηi(i =m，r)表示供应链成员的风险规避度，ηi越大，说明成员越厌恶风险，且ηi0，ηi=0表示成员为风险中性［9］。

(5)社会福利(SW)由消费者和生产者剩余(CS、PS)及政府补贴(S)线性决定［7，8，18］。

πi、E(πi)、U(πi)和Var(πi)分别表示利润、期望利润、期望效用和利润方差，其中i =m，r;Rgp表示绿色产品的绩效价格比，其公式为Rgp=g/p［19］;上标d 和c 分别表示三阶段和两阶段博弈模型，上标*表示结果最优性;下标1、2、3、4分别表示ηm，ηr＞0、ηm＞0，ηr=0、ηm=0，ηr＞0 和ηm，ηr=0 四种情境;下标m 代表制造商，下标r 代表零售商，下标sc 表示供应链系统。

由以上假设及均值－方差理论［9，20］得风险规避制造商和零售商的期望效用函数为

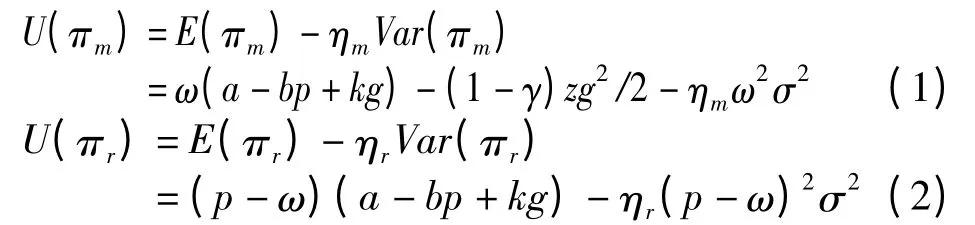
期望社会福利为

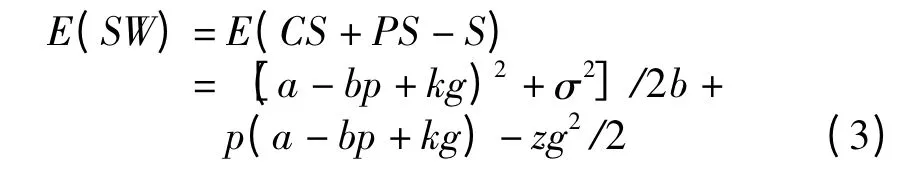
3 模型求解及分析

3.1 三阶段博弈模型

三阶段博弈中，制造商和零售商分散决策，分别以各自利润最大化为目标。求(2)式对p 的二阶偏导数得2U(πr)/p2= －2(b+σ2ηr)＜0，即U(πr)是关于p 的严格凹函数。求(2)式对p 的一阶偏导数并令其等于0 得

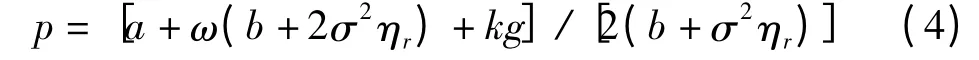
将(4)式代入(1)式求U(πm)的Hessian 矩阵，其一阶主子式和行列式的值分别为| H1| =－A/(b+σ2ηr)，| H | = z (1 － γ)A/(b + σ2ηr)－k2(b+2σ2ηr)2/［4(b +σ2ηr)2］，其中A =2σ2ηm(b +σ2ηr)+b(b +2σ2ηr)。因假设z 是一个较大的正常量，且本文认为z 能满足4z(1 － γ)(b + σ2ηr)·A ＞k2(b+2σ2ηr){(b+2σ2ηr)+2b2E2/(BC)}，其中B=4σ2ηm(b+σ2ηr)+b(b+2σ2ηr)，C=4σ2ηm(b+σ2ηr)·(3b+2σ2ηr)+b(b+2σ2ηr)(7b+6σ2ηr)，E=4σ2ηm(b+σ2ηr)+ (3b + 2σ2ηr)(b + 2σ2ηr)，则4z(1 － γ)·(b+σ2ηr)A ＞k2(b+2σ2ηr)2成立，可知|H| ＞0，故U(πm)是关于ω 和g 的联合凹函数。

运用逆向归纳法求解，代(4)式入(1)式，对其求关于ω 和g 的一阶偏导数并令其等于0，联立方程组可得此时批发价格和绿色度，将其带入(4)式求得此时的零售价格

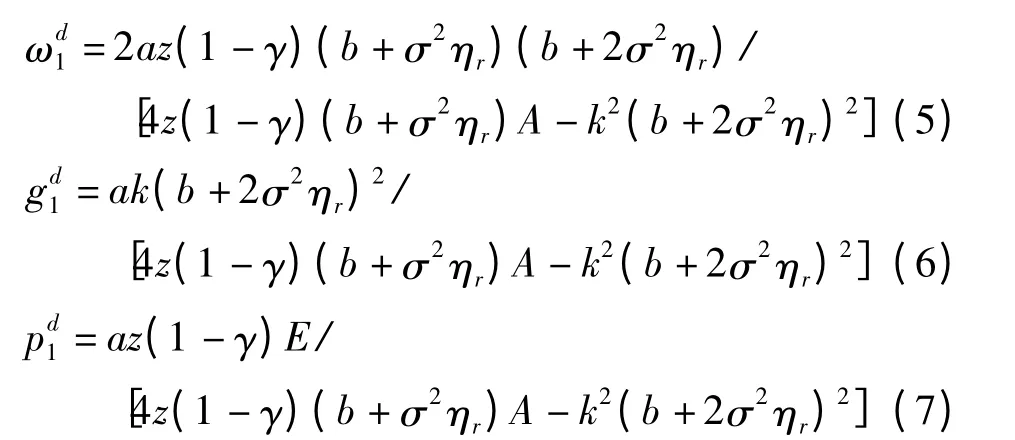
将(6)、(7)式代入(3)式，求对γ 的一阶偏导数并令其等于0，求得最优补贴比例为

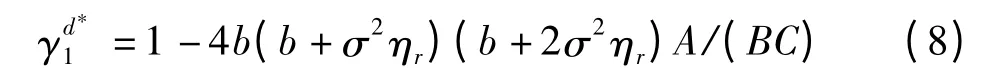
将(8)式代入(5)至(7)式，得最优补贴系数确定后的最优批发价格、产品绿色度和零售价格

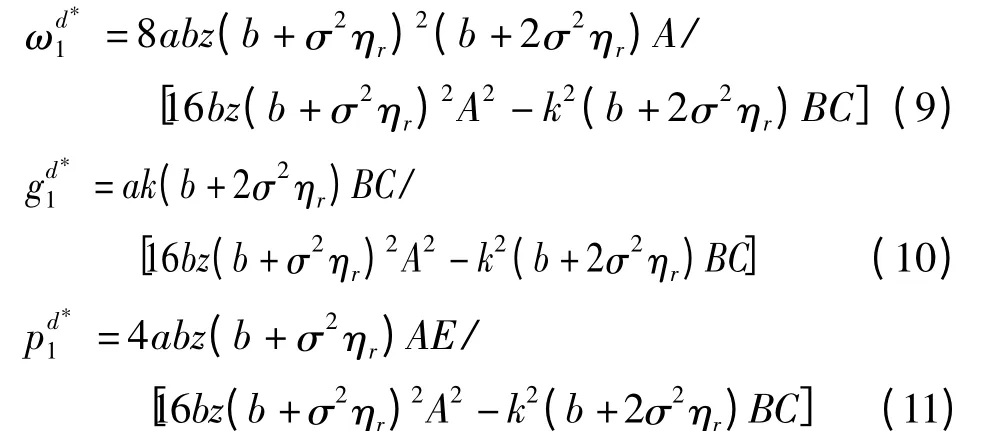
将(8)式至(11)式代入(1)式至(3)式，可得此时制造商和零售商的最大效用及最大期望社会福利

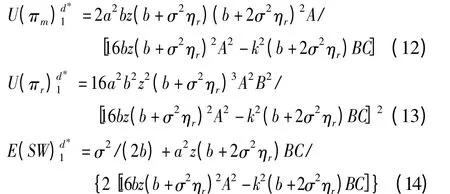
按照相同的范式，可得情境2、3 和4 中的相关最优决策及收益，汇总如表1 所示。

表1 三阶段博弈模型中风险规避度不同时供应链决策及期望效用、期望社会福利

续表1

3.2 两阶段博弈模型

两阶段博弈模型中，制造商和零售商合作决策，他们在综合考虑收益和风险的基础上，选择合适的批发价格和零售价格来促进供应链系统的效用最大化。参考叶飞和林强［21］，江世英等［9］的研究，集中决策模式下考虑成员风险规避的供应链系统期望总效用函数为

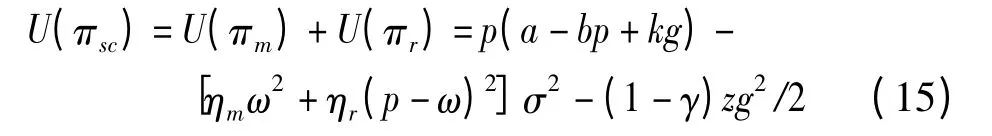
分别求(15)式关于p，ω 和g 的混合二阶偏导数，得其三阶Hessian 矩阵，其一阶主子式值|H1| = －2(b+σ2ηr)＜0，二阶主子式值|H2| =4σ2F ＞0，其中F=ηm(b+σ2ηr)+bηr，其行列式值|H| = －2σ2［2z(1 －γ)F －k2(ηm+ηr)］，因假设z是一个较大的正常量，且本文认为z 满足2bz(1 －γ)＞k2，则|H| ＞0 成立，故U(πsc)是关于p，ω 和g的联合凹函数。

运用逆向归纳法求解，对(15)式求关于p、ω和g 的一阶偏导数并令其等于0，联立方程组有

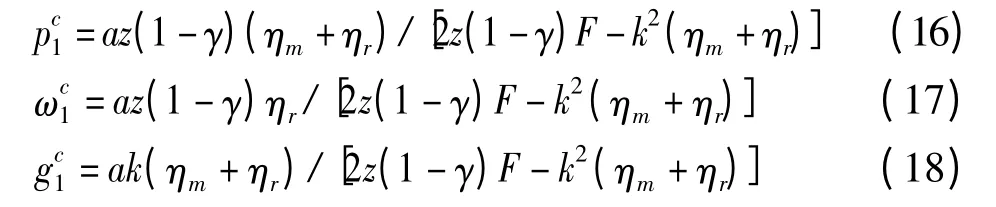
代(16)式、(18)式入(3)式，对γ 求一阶偏导数并令其等于0，求得此时的最佳政府补贴系数=1 －2b(ηm+ ηr)F/(GH)，其中G = ηm(b +2σ2ηr)+bηr，H=ηm(3b+2σ2ηr)+3bηr。

代γc*1 入(16)式至(18)式，可得此时最优定价和绿色度

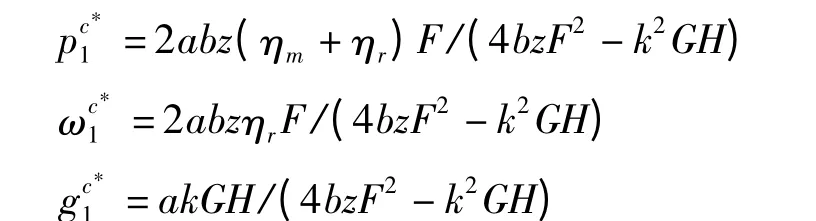
由此可得供应链系统效用和期望社会福利

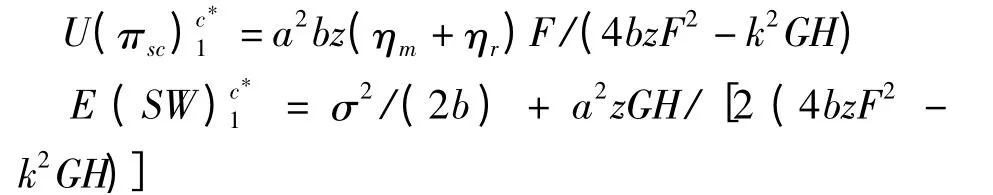
按照情境1 相同的范式，可得情境2、3 和4 中的相关最优决策及收益

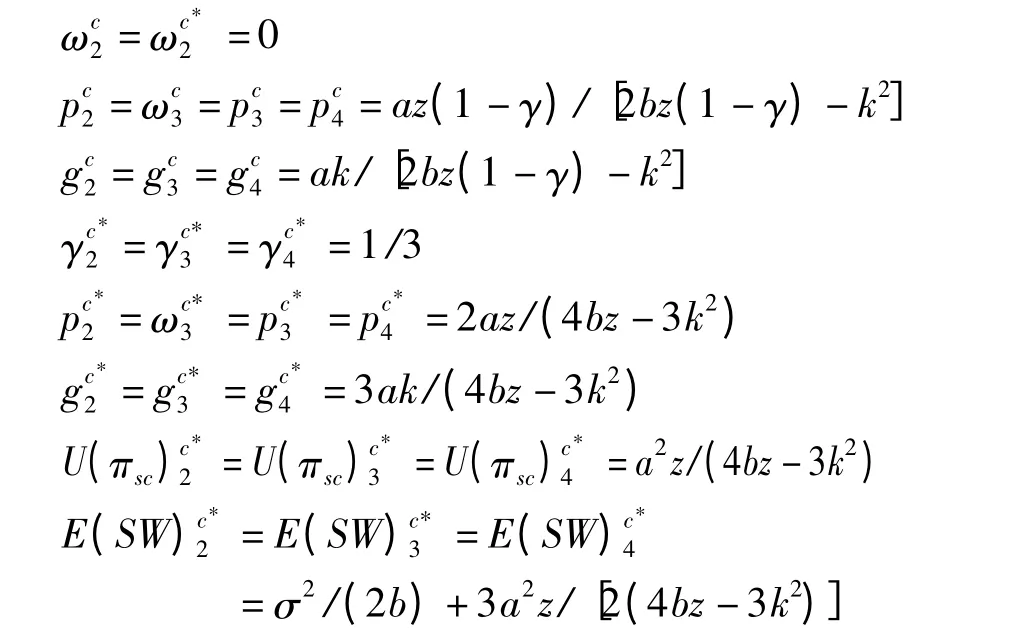
3.3 模型比较与分析

结论1 三阶段博弈模型中，制造商完全风险规避时，制造商无利可图(ηm→∞，ωd*=0);零售商完全风险规避时，零售商无利可图(ηr→∞，pd*=ωd*);制造商和零售商都完全风险规避时，均无利可图(ηm，ηr→∞，pd*=ωd*=0)。据此可判断现实中不存在制造商或零售商完全风险规避的情形。

结论2 无论何种决策条件下，随着政府补贴系数(γ)提升，产品绿色度(g)、产品批发价格(ω)和零售价格(p)都随之增加，同时也能促进绿色产品绩效价格比(Rgp)增大。

结论2 表明政府补贴政策对制造商加大绿色产品研发投入具有激励作用。产品绿色度提升会导致制造商研发成本增加，制造商会将此部分成本转移至零售商，即提高批发价格，零售商将此部分成本转移至消费者，即提高零售价格。此外，政府补贴系数带来的产品绿色度增加幅度大于产品零售价格增加幅度，对于消费者而言，政府补贴有助于消费者获得高绩效价格比的绿色产品。

结论3 三阶段博弈模型中，制造商和零售商风险规避度(ηm，ηr)越高，产品绿色度(g)增大、零售价格(p)降低;制造商风险规避度(ηm)对产品批发价格(ω)产生负向影响、对政府补贴系数(γ)产生正向影响，零售商风险规避度(ηr)对(ω，γ)二者的影响方向相反。最优决策量(ω，g，p，γ)在四种情境下满足的关系汇总如表2。(注:情境2 与情境3 不具有直接可比较性，计算时发现情境2 与情境3 最优决策量大小关系依赖于ηm和ηr的大小关系，而在这两种情境下，ηm和ηr的大小关系相反。)

表2 三阶段博弈模型中风险规避度的影响及结果比较

从结论3 可以看出:(1)制造商风险中性时批发价格大于其风险规避时的情形，零售商风险规避时批发价格大于其风险中性时的情形，批发价格在制造商风险中性、零售商风险规避时达到最大，制造商风险规避、零售商风险中性时最小。显然，制造商和零售商的议价能力会随着他们风险规避程度的提高而减弱。(2)制造商或零售商风险规避时最优绿色度大于他们风险中性时的情形，而最优零售价格小于风险中性时的情形，同时风险规避时的产品绿色度最高、零售价格最低，风险中性时的产品绿色度最低、零售价格最高。说明风险规避的制造商和零售商会通过提高绿色度和降低零售价格来提高份额进而规避风险。(3)制造商风险规避时政府补贴系数大于其风险中性的情形，且在制造商风险规避和零售商风险中性时最大。制造商风险规避时的议价能力比其风险中性时弱，而零售商风险中性时的议价能力比其风险规避时强，此时，制造商对政府补贴的需要强度最高。

结论4 两阶段博弈模型中，最优产品绿色度(g)、政府补贴系数(γ)和期望社会福利(E(SW))与制造商和零售商的风险规避度(ηm，ηr)成正比，最优零售价格(p)、期望总效用(U(πsc))与其(ηm，ηr)成反比。最优决策量(g，p，γ)、期望总效用(U(πsc))和期望社会福利(E(SW))在四种情境下的大小关系总结如表3 所示。

表3 两阶段博弈模型中风险规避度的影响及结果比较

由结论4 可知，在集中式决策模式下，制造商和零售商的风险规避度对最优决策量、期望效用及期望社会福利的影响方向一致，供应链成员风险厌恶程度提升，会促进绿色供应链向消费者提供绿色度更高、价格更低的产品，致使制造商和零售商的期望总效用有所降低。以更具性价比的方式向消费者提供产品是集中式决策模式下绿色供应链成员规避风险的重要举措，且这一举措能够增进社会福利。集中决策模式下当制造商或零售商中的某一成员为风险中性时，另一成员风险规避程度的高低对最优决策、期望效用和福利都不产生影响;相较于制造商和零售商同时风险中性的情形，当他们同时风险规避时，政府应该制定更高水平的补贴系数。

结论5 比较三阶段和两阶段博弈模型，四种情境下最优决策量(g，p，γ)间大小关系如表4 所示。

表4 两种决策条件下最优决策量比较

结论5 表明，无论何种情境，集中决策条件下的最优产品绿色度更高，产品零售价格和最优政府补贴系数更低。制造商和零售商合作决策时，投注于产品绿色度提升的力量相较于制造商独立研发的情境更强，且合作式决策产生的中间协作成本更低，使更为经济地向消费者提供绿色产品成为可能。此外，制造商和零售间的相互协作有助于降低渠道成员对政府激励的依赖程度，增强自主性。

4 数值仿真

假定a =100，b =2，k =1，z =10，σ =2，ηm=0 ～2，ηr=0 ～2［5，9，21］，设置的参数满足关于参数间关系的假设。通过Matlab 软件绘图，探讨政府补贴系数及风险规避对期望总效用和社会福利的影响。

(1)政府补贴系数的影响。假定已知风险规避度(令情境1:ηm，ηr=0. 5;情境2:ηm=0. 5，ηr=0;情境3:ηm=0，ηr=0.5;情境4:ηm，ηr=0)，最优政府补贴系数未确定时供应链系统期望总效用和社会福利如图1 和2 所示。

由图1 可知，无论何种决策结构及何种风险规避情境下，供应链系统期望总效用都随着政府补贴系数的增加而增加。由图2 可知，期望社会福利并不会一直随政府补贴系数的增加而提升，当政府补贴系数超过一定值时，政府补贴系数增加会导致社会福利下降。原因在于此时政府存在过度激励倾向，产品绿色度过度提升带来成本大幅上升，最终显现在产品价格的过度增长上，使得多数消费者处于无力购买的境地，消费者利益被侵蚀，且消失的消费者剩余以及政府补贴成本的增加超过了此时供应链系统期望总效用的增加部分，社会福利则呈现下降趋势。综合图1 和2 可知，当制造商和零售商都存在一定程度的风险规避时，适度的政府补贴(例如ηm，ηr=0.5 时0.63，0.81)，将有利于促进供应链系统收益增长和整体社会福利提升，且集中决策模式下的期望总效用及期望社会福利都大于分散决策模型中的相应值，这说明供应链协调具有期望效用和期望社会福利增进效应。此外，集中式决策模式下，同样的效用和期望社会福利增进效应对政府补贴系数的要求更低，相对较小的政府补贴系数即可达到分散决策模型中同样的效用和期望社会福利。

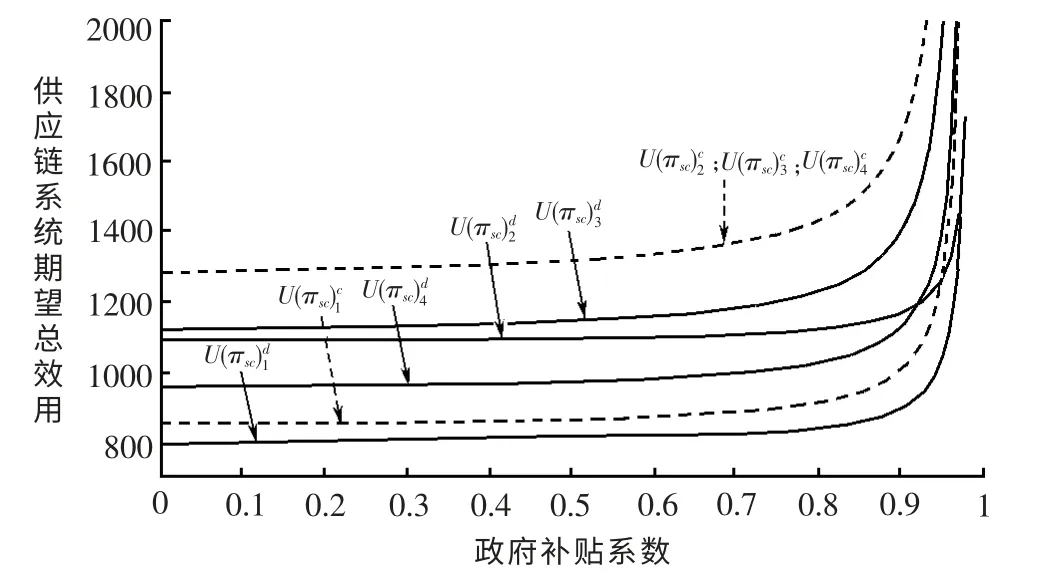
图1 政府补贴系数对供应链期望总效用的影响

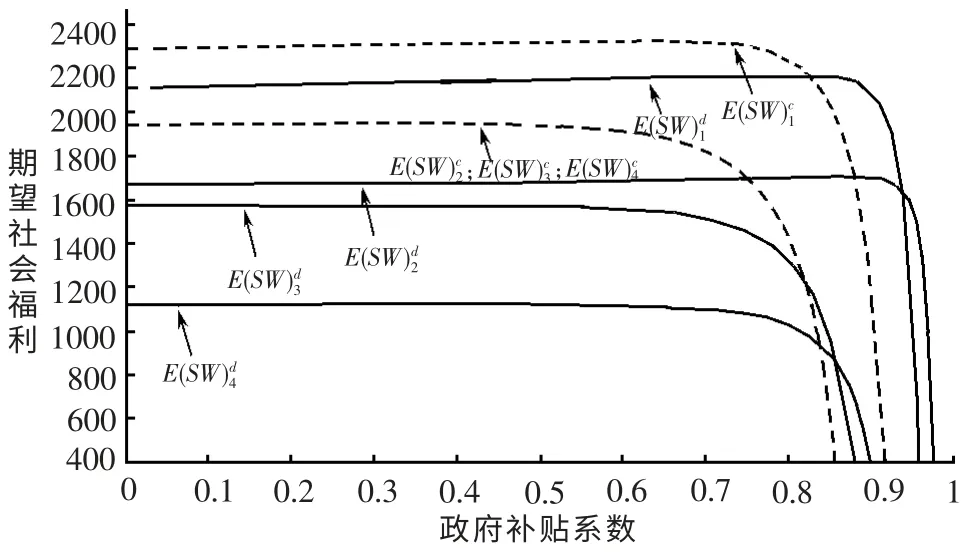
图2 政府补贴系数对期望社会福利的影响

(2)风险规避的影响。鉴于前文已讨论了两阶段博弈模型中风险规避对供应链系统期望效用和期望社会福利的影响，此部分聚焦于三阶段博弈模型。假定已知零售商或制造商一方的风险规避度(ηi=0，ηi=1，ηi=0.8 或ηi=2)，三阶段博弈模型中供应链系统期望效用和期望社会福利如图3 和4 所示。

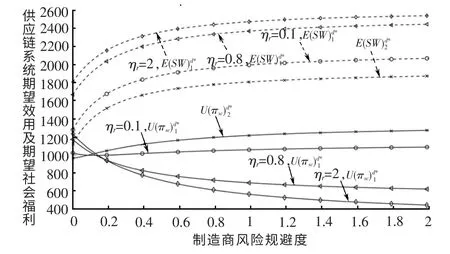
图3 制造商风险规避度的影响

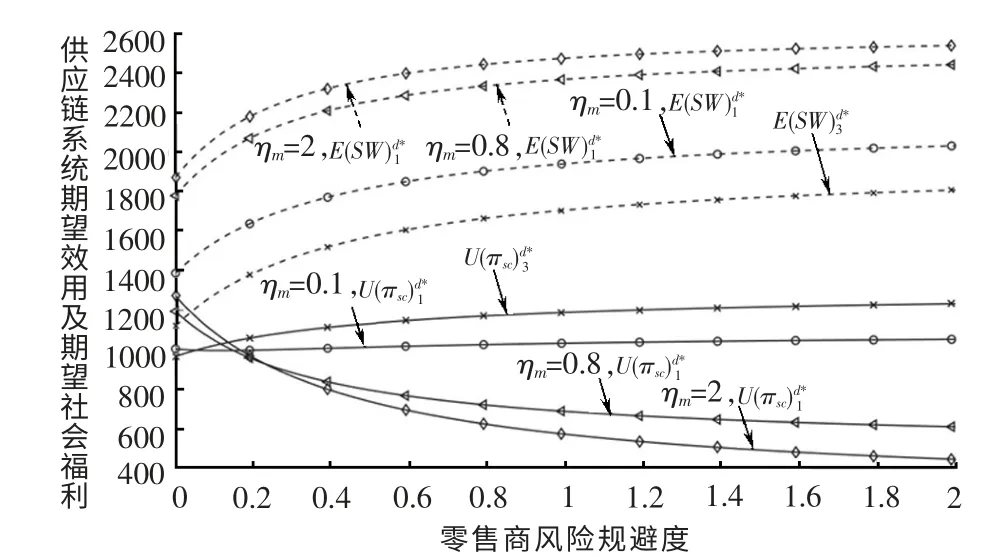
图4 零售商风险规避度的影响

由图3 和图4 可知，制造商和零售商风险规避度影响期望效用及期望社会福利的方向一致。二者对供应链系统总期望效用的影响取决于风险规避度的高低。当制造商或零售商其中一方风险中性时(ηm=0 或ηr=0)，另一方风险规避度的上升会促进供应链系统总效用增加;当制造商或零售商其中一方风险规避度较低时(例如ηm=0. 1 或ηr=0.1)，另一方风险规避度的影响甚微;当制造商和零售商风险规避度都较大时，供应链系统总效用随着零售商或制造商的风险规避度增加而下降。原因在于如若制造商或零售商都趋近于风险中性，他们没有较强的动力去研发如何更经济地向消费者提供绿色产品，此时产品绿色度较低、价格较高，市场需求有限，供应链收益较低，此时任何一方风险规避度的小范围提升有助于激励供应链成员去研发更符合市场需求的绿色产品，增进供应链系统期望效用。然而如果双方都具有较高的风险规避度，此时对风险的高估容易导致与市场需求不符的产品定位，过度强调绿色产品的高绿色度和经济性会侵蚀供应链收益，降低供应链期望效用。

此外，制造商和零售商的风险规避度对期望社会福利都产生正向影响。当制造商和零售商的风险规避度增长到一定值时，期望社会福利趋于稳定，不再呈现明显的增长趋势。说明适度的风险规避，有助于绿色供应链系统实现企业责任和社会责任的平衡，在为消费者提供更具经济性的绿色产品的同时，实现企业收益的增长。

5 结论与启示

在政府与由一个制造商和一个零售商组成的二级绿色供应链间的博弈模型中，考虑制造商和零售商不同风险规避度的四种情境(ηm，ηr＞0、ηm＞0，ηr=0、ηm=0，ηr＞0、ηm，ηr=0)，建立并求解了分散和集中两种决策条件下的均值－方差模型，分析了最优决策、效用和社会福利等结果对政府补贴系数和成员风险规避度的敏感性，研究结果表明:

(1)无论何种决策条件和风险规避情境下，产品绿色度、批发和零售价格、绩效价格比和供应链系统期望效用都随政府补贴系数的增加而增加;适度的政府补贴有助于增加整体社会福利，当政府补贴系数超过一定值时，期望社会福利会下降。

(2)制造商和零售商分散决策时，产品绿色度、期望社会福利都随供应链成员风险规避度的上升而增加，零售价格随之下降;产品批发价格随制造商风险规避度的上升而下降，随零售商风险规避度的上升而增加，而最优政府补贴系数变化与之相反;当制造商和零售商其中一方为风险中性时，另一方风险规避度增加会带来供应链系统效用上升;当制造商和零售商都属于风险规避型时，二者风险规避度的上升都会带来供应链系统效用的下降。

(3)制造商和零售商集中决策时，风险规避情境下零售价格和供应链系统期望效用随成员风险规避度的上升而下降，产品绿色度、政府补贴系数和期望社会福利随成员风险规避度的上升而增加;当制造商和零售商其中一方为风险中性时，另一方风险规避度对相应最优决策和收益无影响。

(4)相较于分散决策而言，制造商和零售商集中决策时产品绿色度更高、零售价格更低、政府补贴系数更低、供应链系统期望效用更高、期望社会福利更高。

本研究的管理启示在于:(1)政府补贴有助于激励生产高绩效价格比的绿色产品，且对供应链系统效用产生有利影响。对于政府而言，通过财政补贴为绿色供应链发展提供资金支持在现阶段不可缺位，但由于过度补贴会引致整体社会福利下降，且供应链成员的风险规避特性也会对最佳补贴比例产生影响，政府需要在将补贴比例控制在一定范围内的基础上根据补贴对象特征设置合理的补贴比例，相较于风险规避程度低的制造商而言，应该给予高风险规避的制造商更高的补贴比例。(2)面对风险规避型制造商或零售商时，零售商或制造商风险规避程度对零售价格和期望效用都产生负面影响，此时积极利用历史数据预测需求进而降低不确定性引起的风险是必不可少的重要措施。(3)面对风险中性制造商或零售商时，分散决策情境下，零售商或制造商风险规避程度对供应链系统效用都具有积极影响，此时适度提升自身的风险规避度，保持更高的市场警惕性是必要的。(4)无论何种风险规避情境下，制造商和零售商集中决策比分散决策会带来对企业、对消费者和对社会而言都更有利的结果。因此，采取合作决策的方式，是促进绿色供应链实现可持续发展的重要举措。然而，当供应链成员有一方是风险中性时，采取合作决策时应注意利益分配。

本文聚焦的供应链系统主要由一个制造商和一个零售商组成，但现实中的供应链网络结构通常较为复杂，涉及多个制造商和多个零售商的绿色供应链管理及政企博弈问题在未来也值得拓展;此外，本研究只验证了风险规避情境下集中决策相较于分散决策而言的更优性，但是对于制造商和零售商间的合作机制并没有进一步探索，是今后值得研究的方向之一。