具有miRNA调控的癌症网络模型的动力学分析

许慧洁，易秀，杨晓燕，王乔钰

(兰州交通大学 数学系，甘肃 兰州 730070)

1 引言

在细胞中，生物的遗传信息被储存在DNA中，DNA被世代传递。为了深入了解这些过程，数学模型一直被用于基因调控网络的研究。但是最近的研究表明，只有大约2%的基因序列可以被表达成蛋白质，因此在建立遗传调控网络的数学模型时，还需要考虑一些别的因素，近年来越来越多的研究揭示了ncRNA在人体中的重要作用，而本文所考虑的miRNA簇是一种特殊的ncRNA。本文所讨论的模型是基于文献[1]的系统(1)：

(1)

其中，u表示Myc和E2F混合物的种群密度，v表示miRNA簇的种群密度，并且假设模型中出现的所有参数对于生物学来说都是有意义的(即都是正的)。常数σ表示通过细胞外介质中的转录途径产生的蛋白质，δ表示蛋白质的降解速率，μ表示独立于Myc和E2F的miRNA的转录，k2是蛋白质的转录速率，r是miRNA降解的速率。当作者引入变量后，减少了参数，得到了系统(2):

(2)

当我们考虑时滞对系统(1)的影响后，便得到了下面系统(3)：

(3)

假设E*=(u*,v*)是系统(2)的正平衡点，很容易得到v*=u*+1，且u*,v*是关于u的方程G(u)=u3+m2u2+m1u+m0的正根，其中m0=-α(a+b)m1=α+b(1-α),m2=b-(α+k)。在文献[1]中，关于系统(2)的正平衡点得到了以下结论：

Ⅰ 当系统(2)只有一个正平衡点时，这唯一的正平衡点E*在0<β<β0，是渐近稳定的。当β<β0时，E*是不稳定的，当β=β0时，系统(2)在E*附近进行Hopf分支。

Y.L.Song等在实验中观察到了miRNA对Myc和E2F的抑制作用具有一定的时间延迟，并且Myc和E2F在自我促进时信号的传输需要时间；Song等人针对这一实验现象，提出了时滞微分方程，并给出了正平衡解的存在性，全面分析了双稳态的动力学。T.H.Zhang[2]等研究了一个具有时间延迟的基因表达模型，并给出了存在导致Hopf分支的时间延迟临界值。Nikolov[3]等人给出了时间延迟在miRNA动力学的调节中以及别的调节网络中更具有稳定性的作用，但是，他们没有彻底研究这种稳定作用取决于延迟的长度。因为miRNA在多种细胞形成的过程中起着重要的作用，因此很多数学家通过建立数学模型来研究miRNA与癌症细胞之间的关系，如想要对此模型有更多的了解可以参考文献[4-8]。本文考虑实验中另外的时间延迟现象，即考虑蛋白质在转录和降解的过程中存在的时间延迟会对系统稳定的正平衡解产生的影响。

2 时滞引起的稳定的平衡点失稳

这部分主要研究系统(2)只有一个正平衡解时，且这个正平衡解是稳定的情况下时滞对于这个正平衡解产生的影响。

用E*=(u*,v*)来表示系统的正平衡解，将系统(3)在E*处线性化可得：

(4)

其中

线性化系统的特征方程为：

λ2+(1-βA)λ-βA+β(λ+1-B)e-λτ=0

(5)

我们假设λ=iω(ω>0)是特征方程的根，将λ=iω代入特征方程得到以下方程

-ω2+(1-βA)iω-βA-β(cosωτ-isinωτ)iω+β(1-B)(cosωτ-isinωτ)=0

将上述方程分离实部和虚部，可得下列方程组：

(6)

整理可以得到：

ω4+(1+β2A2-β2)ω2+β2(A2-(1-B)2)=0

(7)

令Z=ω2，则式(7)可化为：

Z2+(1+β2A2-β2)Z+β2(A2-(1-B)2)=0

从上式很容易得到下面引理：

定理1当Δ=(1+β2A2-β2)2-4β2(A2-(1-B)2)>0,1+β2A2-β2<0时，方程(7)有一个正根。

然后由方程组(5)可以得到关于sinωτ和cosωτ的表达式

则τ的值可以得出：

令h(Z)=Z2+(1+β2A2-β2)Z+β2(A2-(1-B)2)=h(ω2)

由文献[9]得

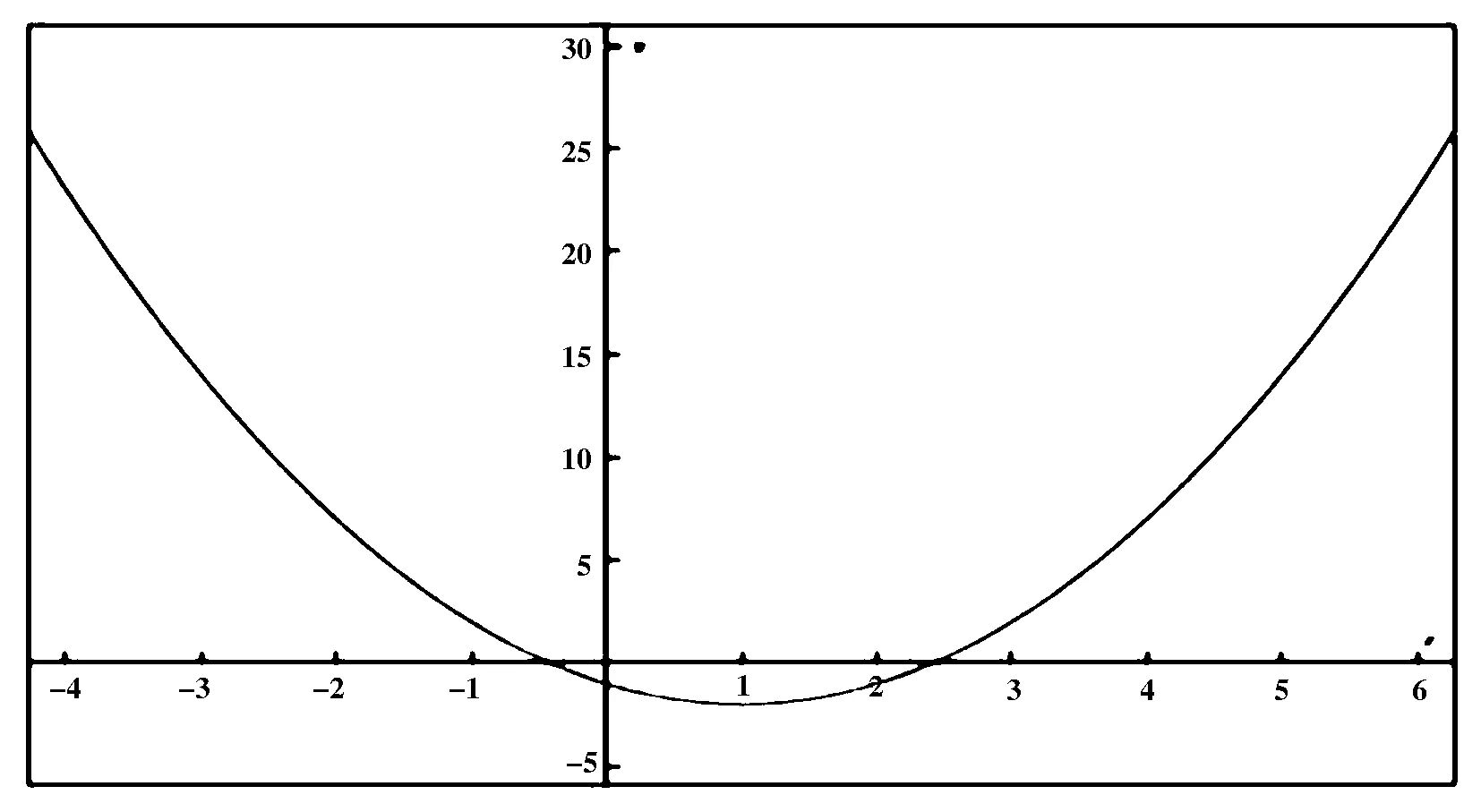
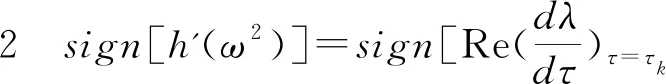
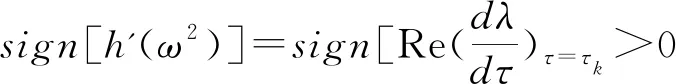
由上述横向性条件得到下面的定理：

定理2假设ω和τj是由式(7)、式(8)定义的,E*是稳定的正平衡解。在条件1+β2A2-β2<0成立的情况下：

(1)对任意的τ∈(0,τ0)时,系统(3)的平衡解E*是稳定的，当τ∈(τ0,+∞)时E*是不稳定的。

(2)当τ=τj(j=0,1,2,…)时，系统(3)在正平衡解E*附近出现Hopf分支。

3 数值模拟

图1当β=50,α=0.18,a=1,b=1.8,k=5时，系统(2)数值模拟图2当β=50,α=0.18,a=1,b=1.8,k=5时，系统(2)有两个正平衡点时的数值模拟

图3当β=50,α=0.18,a=1,b=1.8,k=5时，系统(2)有三个正平衡点时的数值模拟图4当β=5,α=0.5,a=2,b=1,k=5时，系统(2)有一个正平衡点时的数值模拟

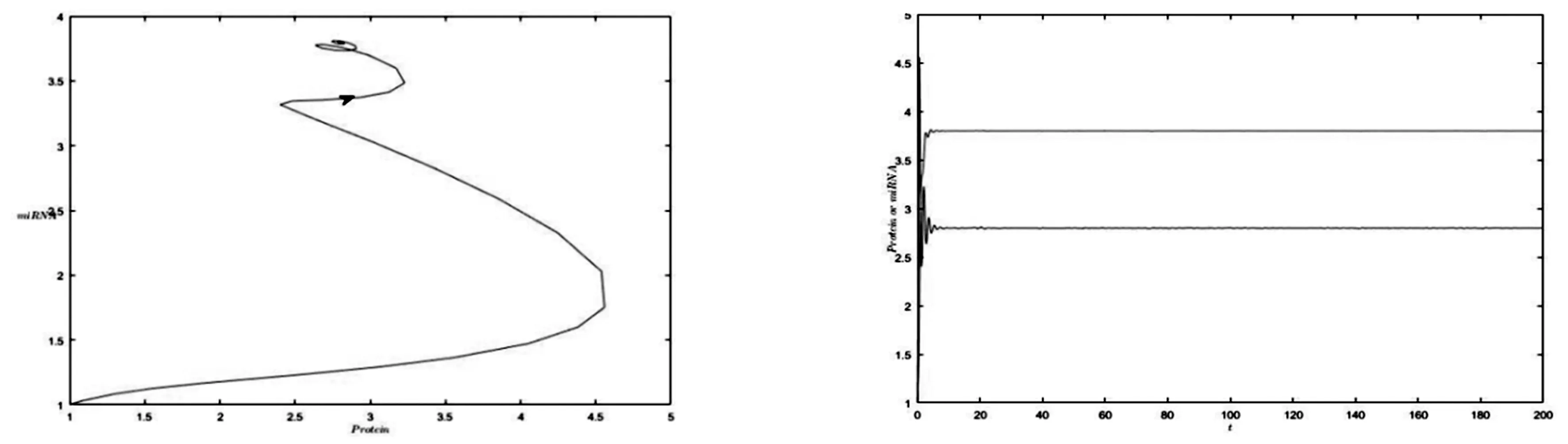
图5当τ=0.18,β=5,α=0.5,a=1,c=1.8,k=5时，系统(3)的相图图6当τ=0.18,β=5,α=0.5,a=1,c=1.8,k=5时，对系统(3)进行的数值模拟

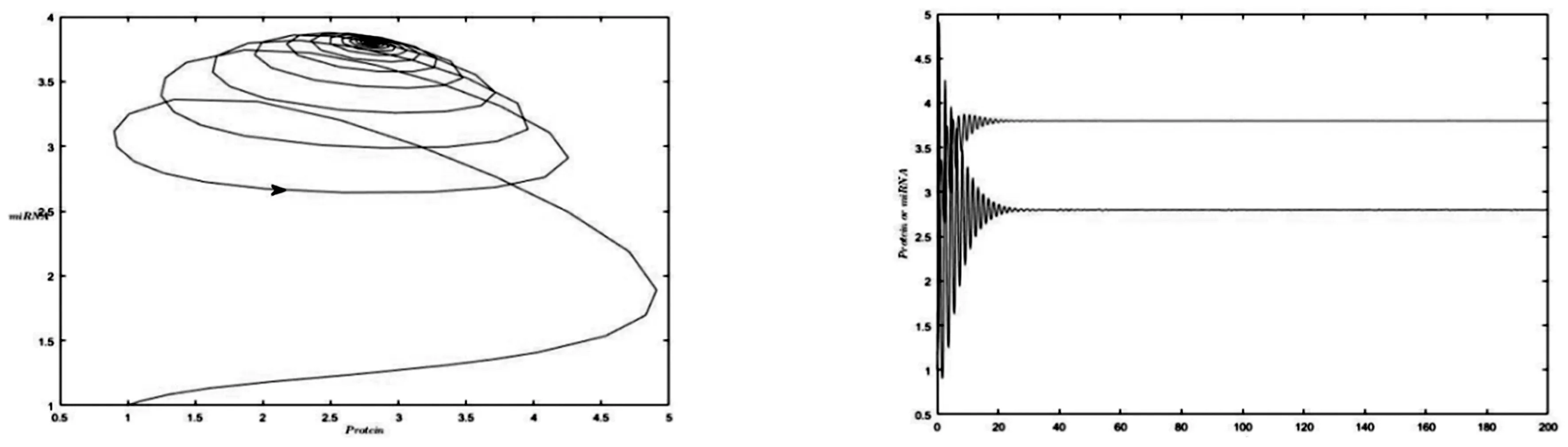
图7当τ=0.2,β=5,α=0.5,a=1,c=1.8,k=5时，系统(3)的相图图8当τ=0.2,β=5,α=0.5,a=1,c=1.8,k=5时，对系统(3)进行的数值模拟

图9当τ=0.21,β=5,α=0.5,a=1,c=1.8,k=5时，系统(3)的相图图10当τ=0.21,β=5,α=0.5,a=1,c=1.8,k=5时，对系统(3)进行的数值模拟

图11当τ=0.3,β=5,α=0.5,a=1,c=1.8,k=5时，系统(3)的相图图12当τ=0.3,β=5,α=0.5,a=1,c=1.8,k=5时，对系统(3)进行的数值模拟

4 结论与讨论

本文主要分析了一个具有miRNA调控的基因表达模型，考虑了存在于蛋白质的转录和降解过程中的时滞，会对系统产生怎样的影响。结果表明：系统(2)仅有一个稳定的正平衡解的情况下，时滞会使系统的正平衡解从稳定变为不稳定。更具体地说，如果平衡解在没有延迟的情况下是稳定的，一个非常小的延迟会使平衡解不稳定，当增加延迟的长度时就可能诱导出稳定的周期解。