基于BSO-OS算法的两阶高维数据特征选择

田浩楠，周 晖

(南通大学 信息科学技术学院，江苏 南通 226019)

0 引 言

随着云计算和大数据的迅速发展，海量数据不断呈现，数据维度不断增加[1]。特征选择从给定特征集合中选取相关特征子集，以降低数据维度、简化学习模型、加速学习过程[2,3]。

高维数据的搜索空间远大于一般数据，其特征选择非常困难[4]。群集智能(swarm intelligence, SI)搜索能力强、鲁棒性好，而被应用于高维数据特征选择。文献[5,6]将位置更新与变异机制以及模糊规则引入二进制PSO(binary particle swarm optimization, BPSO)算法以搜索特征子集。文献[7]采用PSO算法搜索特征子集，该算法引入新的局部搜索机制和重置gbest机制以提高搜索能力。文献[8，9]将PSO算法和过滤式方法相结合来选取特征子集。文献[10]提出一种两阶方法，首先采用F统计量选择特征，然后使用BPSO算法在这些特征中选取最优特征子集。

然而，上述方法存在以下不足：其一，仅采用群集智能选取的特征子集特征数量多，且运行效率差；其二，采用群集智能和过滤式方法相结合选取特征子集，虽然取得良好效果，但没有考虑多特征间的冗余性；其三，两阶方法的第1阶段所选特征数量需人工指定。

针对上述问题，提出基于BSO-OS(brain storm optimization in objective space)的两阶高维数据特征选择算法(two-stage feature selection algorithm for high-dimensional data based on BSO-OS, BSFS)。首先，针对高维数据特征选择问题设计BSO-OS算法，并采用BSO-OS算法搜索分类性能较好、特征数量较少的特征子集；然后，采用快速近似联合互信息(fast approximate joint mutual information, FAMIR)对上述所选特征子集中分类精度最高的特征子集进行特征排序，去除冗余、不相关特征。在6个高维数据集上进行实验，结果验证了所提算法的有效性。

1 BSO-OS算法

BSO(brain storm optimization)是一种新的群集智能算法[11]。该算法模拟人类创造性解决问题的思路和过程，是一种很有潜力的群集智能算法。而BSO-OS算法使用简单分类操作代替BSO算法中的聚类算法，特别适用于解决高维问题[12]。

BSO-OS算法中，新解是对所选解加上高斯随机值而生成，如式(1)所示

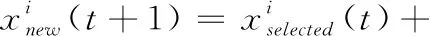
(1)

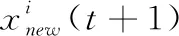
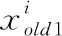
(3)

其中， logsig() 是S型对数传递函数，T为最大迭代次数，t为当前迭代次数，k用来改变logsig() 的斜率， rand() 产生(0,1)间的随机值。

然而BSO-OS算法适用于连续函数优化，而特征选择是组合优化问题，根据高维数据特征选择的特点设计BSO-OS算法。

(1)个体初始化：每一个个体表示一个所选特征子集，个体初始化为：Xi=[x1,…,xi,…,xn]， 其中Xi表示第i个个体，n为特征数量，xi为随机产生的(0,1)间的值表示选择第i个特征的概率。使用式(4)对个体每个维度进行离散化

(4)

(2)个体更新:使用式(1)对个体进行更新，对更新后的个体的每个维度使用式(5)进行离散化

(5)

其中， sig() 是S型传递函数， rand() 产生(0,1)间的随机值。

(3)扰动更新:BSO-OS算法中，扰动更新过程仅改变一个维度的值，这在个体维度很高时并不适用。因此，本文在扰动更新时改变特征数量1%个维度的值，其值改变如式(6)所示

(6)

2 FAMIR

基于信息准则的方法中，推荐使用联合互信息(joint mutual information，JMI)[13]，JMI计算公式为

(7)

其中，Fi是候选特征，Fj是已选特征，S是已选特征集合，Y是类标签。

然而JMI计算复杂度是特征数量的二次方，这限制其在高维数据中的应用。针对上述问题，文献[14]提出JMI快速近似算法即FAMIR，以加速JMI计算。该方法主要思想是对每项I(Fi,Fj;Y) 计算上下界，利用其上下界近似求其值。上界计算公式为

(8)

其中，Q={I(Fi,Fj),I(Fi,Y),I(Fj,Y)}。

下界计算公式为

(9)

因此I(Fi,Fj;Y) 近似计算为

I(Fi,Fj;Y)=β1L(Fi,Fj;Y)+β2U(Fi,Fj;Y)+β0

(10)

其中，β0、β1、β2为参数。

计算候选特征Fi的JMI值时，首先计算前λ项I(Fi,Fj;Y) 的值及其上下界(λ一般取特征数量的5%)，然后采用最小二乘法计算每一个β参数。在随后每项I(Fi,Fj;Y) 计算中使用式(10)近似计算以达到加速目的。

3 BSFS算法

群集智能由于搜索能力强、鲁棒性好而在高维数据特征选择中得到应用，但仅采用群集智能搜索的特征子集特征数量多，而过滤式方法能有效去除不相关和冗余特征，因而提出将群集智能和过滤式方法相结合的BSFS算法。

3.1 适应度函数

个体迭代更新过程中，个体优劣是由适应度函数决定。采用式(11)所示适应度函数对特征子集进行计算，其中μ为加权系数

fitness=μ×balanced_accuracy+(1-μ)×distance

(11)

其中

(12)

其中，n是不同类的数量，TPi是类i中被正确分类的样本数量， |Si| 是类i的样本总数。计算算法产生的候选特征子集的分类性能时采用K近邻算法(K-nearest neighbor，KNN)。

其中

(13)

其中

(14)

(15)

Dis(Vi,Vj) 用于度量向量Vi和Vj之间的距离，采用向量Vi和Vj之间，对应维度值相同的数量除以向量维度的值作为距离值。Db是每个样本与不同类中最近样本之间距离的平均值，Dw表示相同类中每个样本与最远样本之间距离的平均值， |S| 是样本总数。

3.2 算法实现

BSFS算法包括两个阶段：首先采用BSO-OS算法搜索特征子集，再对上述所选特征子集中分类精度最高的特征子集使用FAMIR。BSO-OS算法的具体过程如图1所示，算法中采用式(11)所示适应度函数对所选特征子集进行计算。

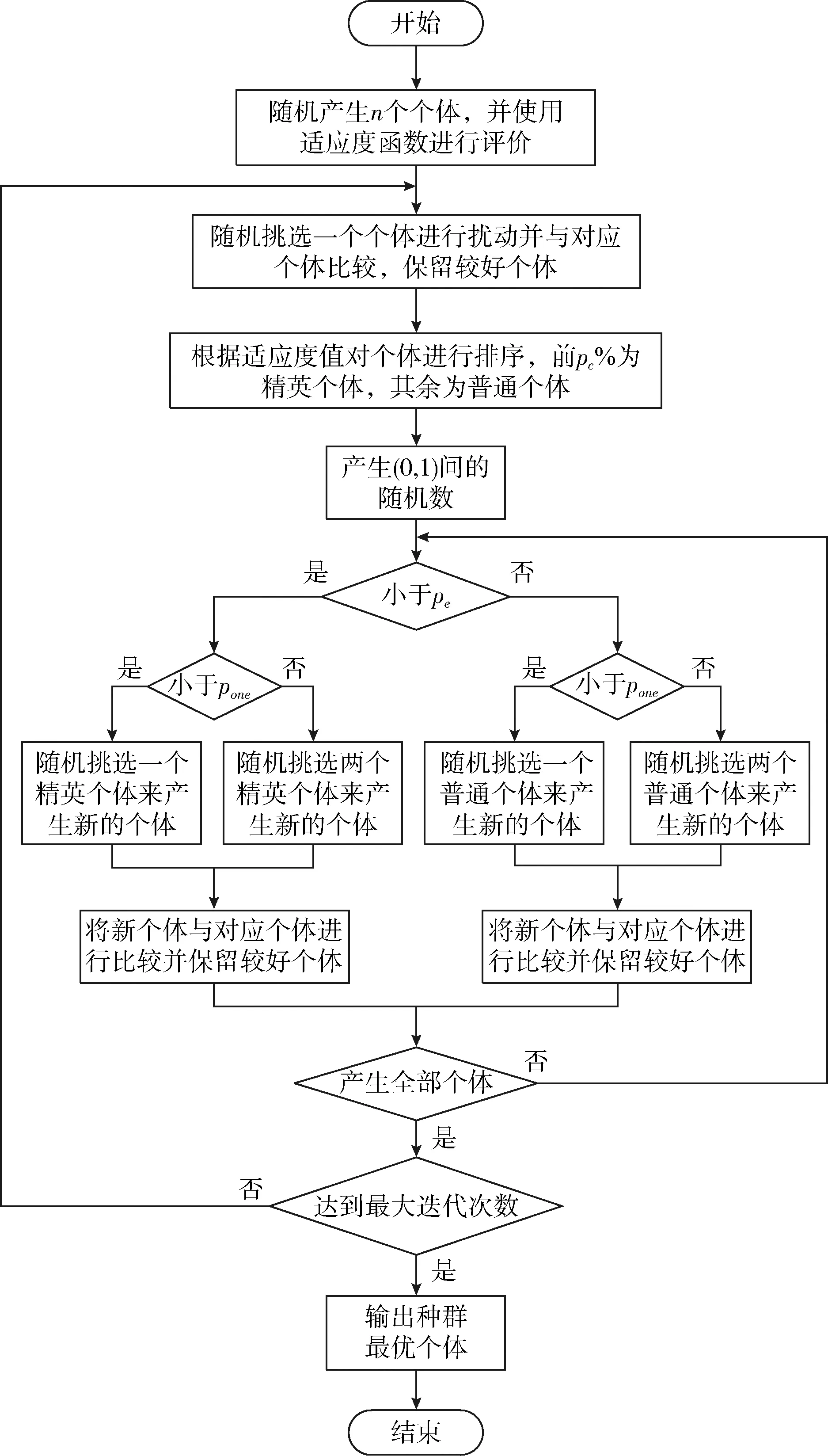
图1 BSO-OS算法的具体过程

4 实验设置和结果分析

4.1 数据集

为了测试所提算法性能，采用6个高维基因表达数据集，数据集信息见表1，数据集可从以下网址下载：http://www.gems-system.org。表1中第5列表示具有最少样本的类其样本占总样本的百分比，第6列表示具有最多样本的类其样本占总样本的百分比。

从表1可见，相比特征数量，数据集样本很少，且具有最多样本的类和具有最少样本的类，其样本百分比差异很大。这些因素导致高维数据集的特征选择非常困难。

4.2 实验配置和参数设置

实验中，采用k=3的KNN算法。计算分类精度时，使用十折交叉验证，其中一折用作测试集，其余用作训练集，最后分类精度取10次测试集上的平均。对于每个数据集，进行30次独立运行。考虑到计算和存储资源，将个体数量n限制为150。实验中，BSO-OS算法参数设置见表2。

4.3 实验结果与分析

本文使用式(11)所示适应度函数，其中参数μ的取值会影响BSO-OS算法所选特征子集的性能，为选取更好μ值，首先比较μ取不同值,即μ取0.5、0.6、0.7、0.8、0.9和1.0时,BSO-OS算法所选特征子集的性能，结果见表3。

在表3中，首先比较每个数据集上μ取不同值时所选特征子集的平均精度和平均特征数量，若平均精度越高同

表1 实验所用数据集

表2 实验参数值

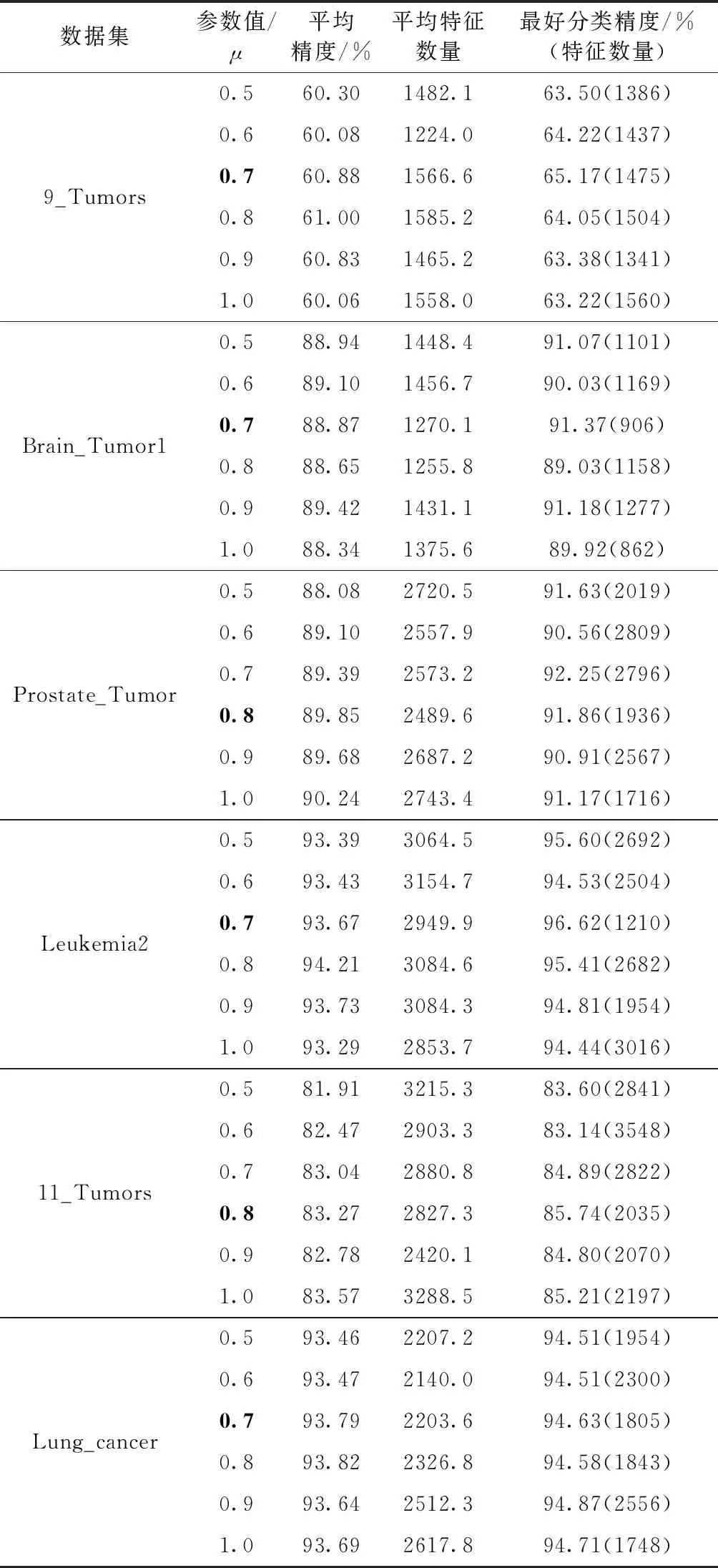
表3 μ取不同值时的实验结果

时平均特征数量越少，则对应μ值越好。但是仅通过平均精度和平均特征数量有时很难区分不同μ值的优劣，因此表3添加最好精度一列，该列表示所选特征子集中获得的最好分类精度，同时给出该精度对应特征子集的特征数量。添加该列进行比较的原因是第2阶段仅对第1阶段所选分类精度最高的特征子集使用FAMIR。若通过平均精度和平均特征数量不能区分μ值优劣，则比较所选特征子集的最好分类精度，最好分类精度越高则对应μ值越好。每个数据集的最好μ值已用粗体标出。从表3可见，μ取0.7时在6个数据集的4个上获得最好结果，μ取0.8时在6个数据集的两个上获得最好结果。为方便起见，所有数据集取相同μ值，因此，下列所有实验取μ=0.7。

表4给出所提算法的实验结果。其中“Full”表示使用数据集的所有特征，“BSO-OS”表示第1阶段采用BSO-OS算法选择的特征子集中分类精度最高的特征子集，“BSFS”表示所提算法的最终结果。从表4可见，所提算法在全部数据集相比原始数据集选出很少特征，同时所选特征子集的分类精度都有提高。在Prostate_Tumor数据集，所选特征子集的特征数量只有原始数据集的2.2%，但分类精度却提高10.6%。除9_Tumors数据集，在其余数据集，所选特征子集的特征数量都不超过原始数据集的10%，同时分类精度都有提高。在11_Tumors数据集，分类精度提高11.2%，但特征数量只有原始数据集的4.9%。图2给出所提算法在每个数据集所选特征子集的分类精度随特征数量的变化，其中横坐标表示所选特征子集的特征数量，纵坐标表示所选特征子集的分类精度。表4还可看出，所提算法中每阶算法的有效性，采用BSO-OS算法选出的特征子集相比原始数据集具有较少特征，同时特征子集的分类精度都有提高，在Leukemia2数据集，BSO-OS算法选出的特征子集的特征数量只有原始数据集的10.8%，但分类精度提高9.4%。对BSO-OS算法选出的特征子集使用FAMIR算法后，可以得到特征数量更少的特征子集，同时特征子集的分类精度都有提高。在Prostate_Tumor数据集，使用FAMIR算法后，特征子集的特征数量减少92.0%，但分类精度略有提高。

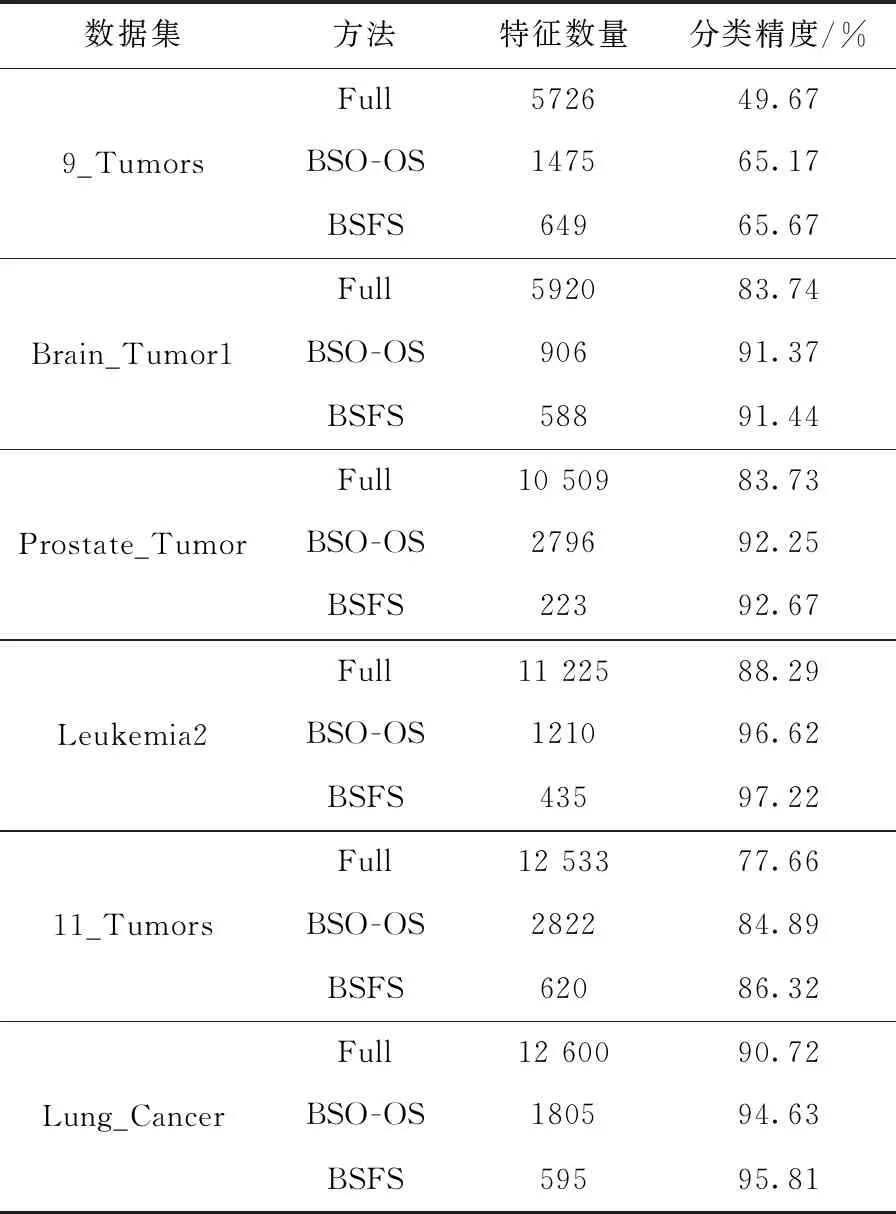
表4 所提算法的实验结果

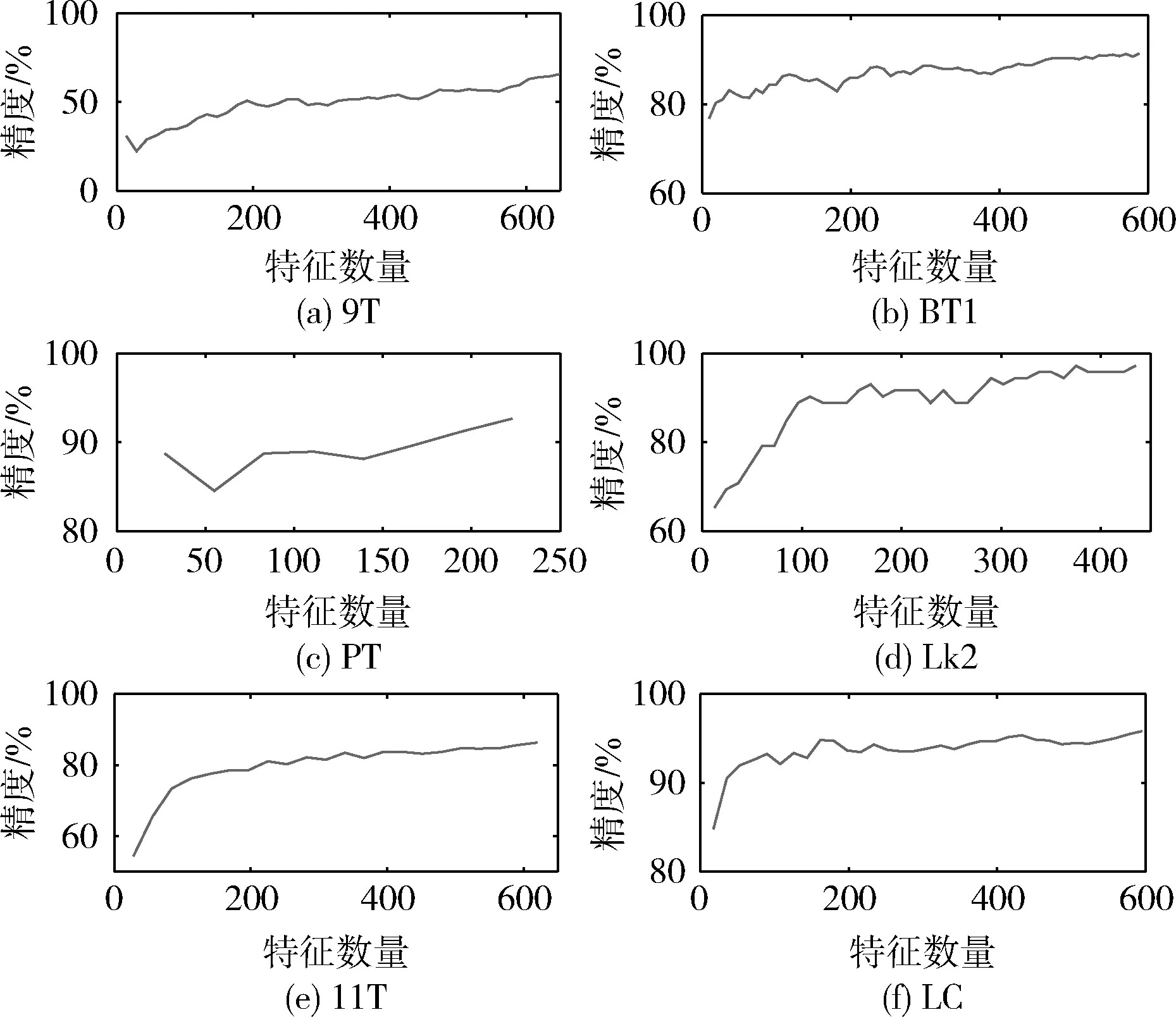
图2 所选特征子集的分类精度随特征数量的变化

本文将BSO-OS算法应用于高维数据特征选择，为验证其有效性，与标准BPSO算法的实验结果进行比较，结果见表5。从表5可见，在全部数据集，采用BSO-OS算法选出的特征子集的平均分类精度和平均特征数量都优于BPSO算法选出的特征子集。在Lung_Cancer数据集，BSO-OS算法选出的特征子集的平均特征数量只有BPSO算法的46.3%，但平均分类精度却提高2.0%。在9_Tumors数据集，BSO-OS算法比BPSO算法选出的特征子集的平均分类精度高11.1%，但平均特征数量却只有BPSO算法的65.1%。同时，将BSO-OS算法与BPSO算法的运行时间进行比较，结果如图3所示，该图中运行时间指的是平均每轮的运行时间。从图3可见，在全部数据集，BSO-OS算法的运行效率都优于BPSO算法，其运行时间分别只有 BPSO 算法的51%，72%，63%，54%，62%，63%。

为进一步验证所提算法的有效性，分别与一阶方法(PSO-LSSU)[8]和两阶方法(CDMC)[10]所选特征子集中分类精度最高的特征子集进行比较。表6给出所提算法与PSO-LSSU和CDMC在6个数据集的实验结果。为与CDMC进行公平比较，在表6的第4行给出所提算法得到与CDMC分类精度相似时的特征子集的特征数量和分类精度，正如“BSFS(*)”一行所示。

从表6可见，与PSO-LSSU的结果相比，在全部数据集，所提算法所选特征子集的特征数量和分类精度都优于PSO-LSSU所选特征子集。与CDMC的结果相比，在6个数据集的4个上所提算法所选特征子集的特征数量和分类精度优于CDMC所选特征子集，在Prostate_Tumor数据集，在分类精度略高的情况下，所提算法所选特征子集的特征数量只有CDMC所选特征子集特征数量的5.2%。在Leukemia2数据集具有与CDMC相似的性能，仅在9_Tumors数据集的性能略差于CDMC。

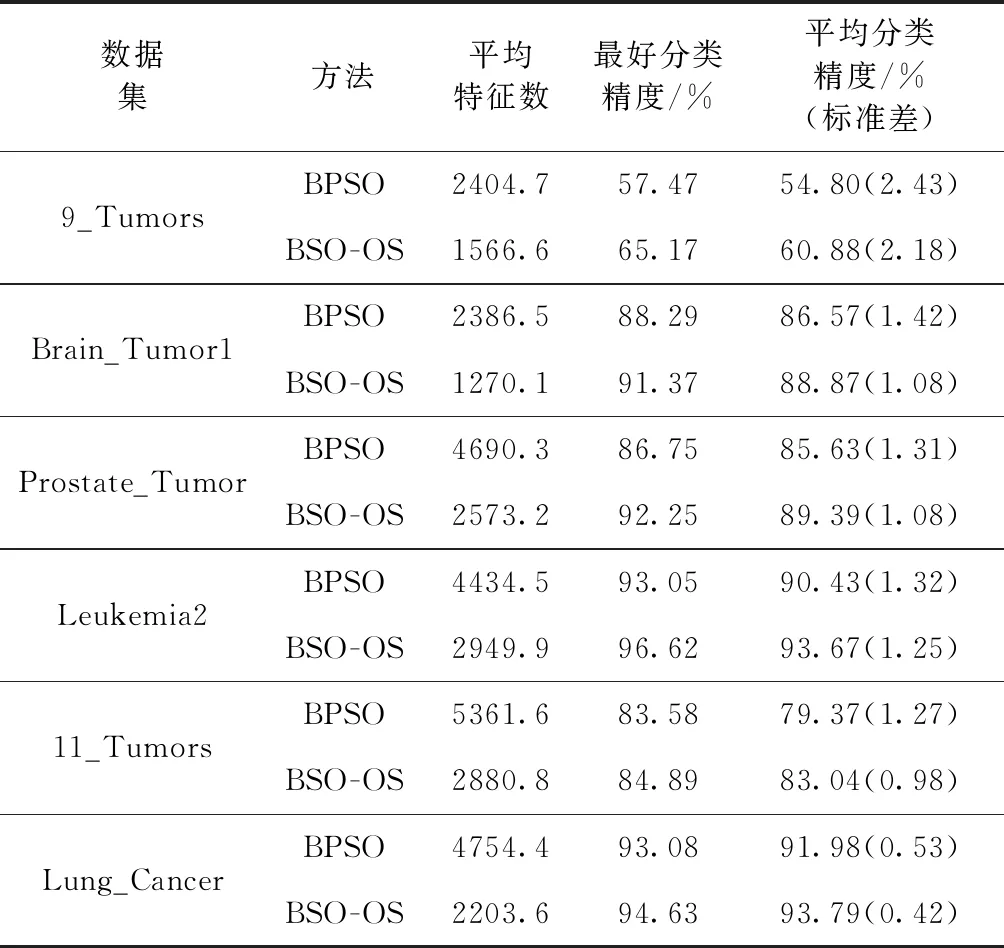
表5 BSO-OS和BPSO的对比结果

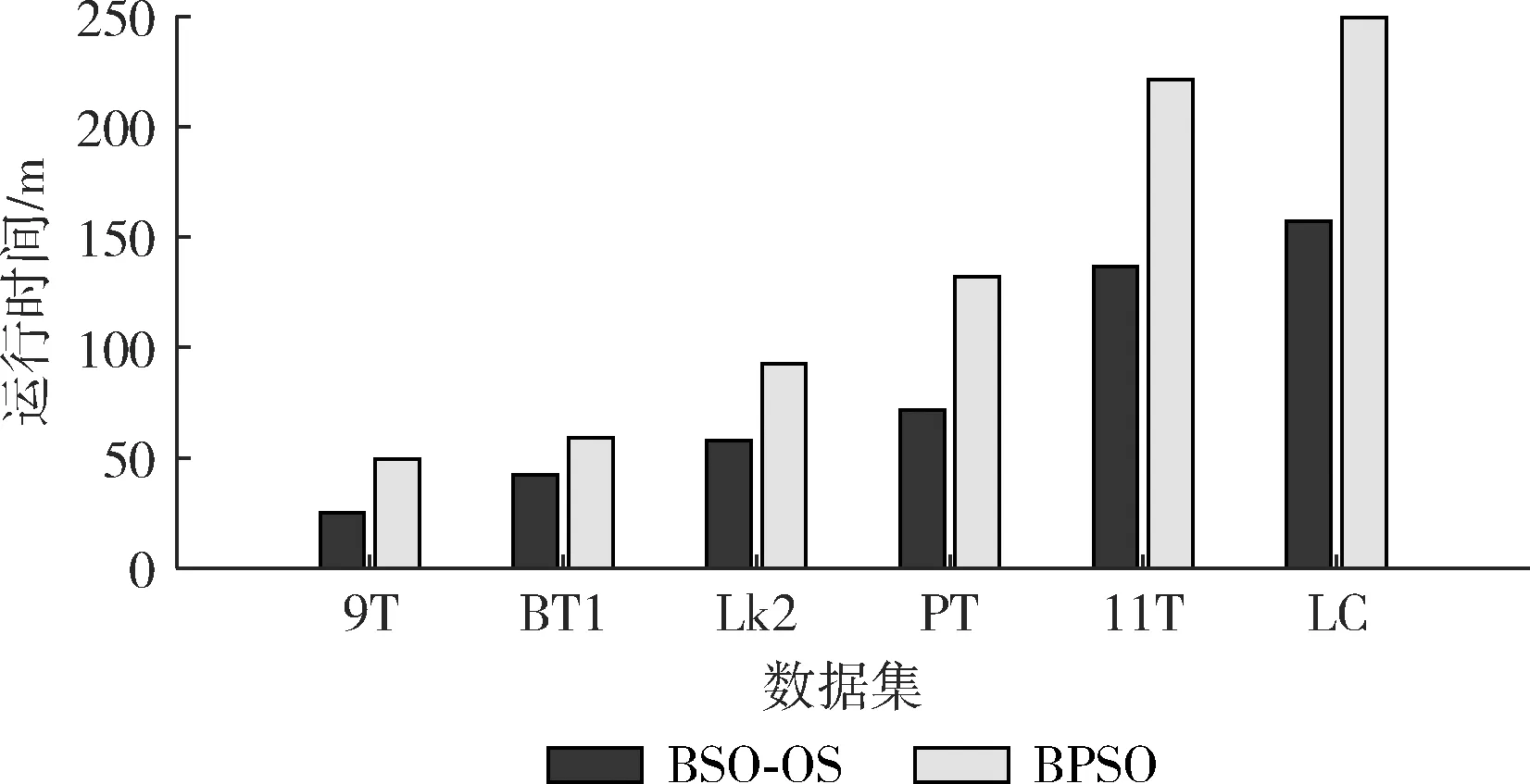
图3 BSO-OS与BPSO运行时间对比

图4给出3种方法各自的运行时间，其中运行时间指的是平均每轮的运行时间。为公平比较，分别将CDMC第1阶段和所提算法第2阶段的运行时间平均到每轮运行时间中。从图4可见，所提算法在全部数据集的运行效率优于PSO-LSSU，与CDMC的运行效率相比，所提算法在6个数据集的3个上运行效率占优，在Lung_Cancer数据集具有类似的运行效率，在Leukemia2和Prostate_Tumor数据集，运行效率略差。

5 结束语

针对高维数据特征选择问题，将BSO-OS和FAMIR算法相结合，提出一种两阶特征选择算法BSFS。实验结果表明：所提算法能有效实现BSO-OS和FAMIR两者的优势互补，在第1阶段，BSO-OS算法在高维数据特征选择中具有更好的搜索能力和运行效率；在第2阶段，FAMIR算法能有效去除特征子集中的不相关和冗余特征。整个算法分类精度高，同时具有良好的运行效率。

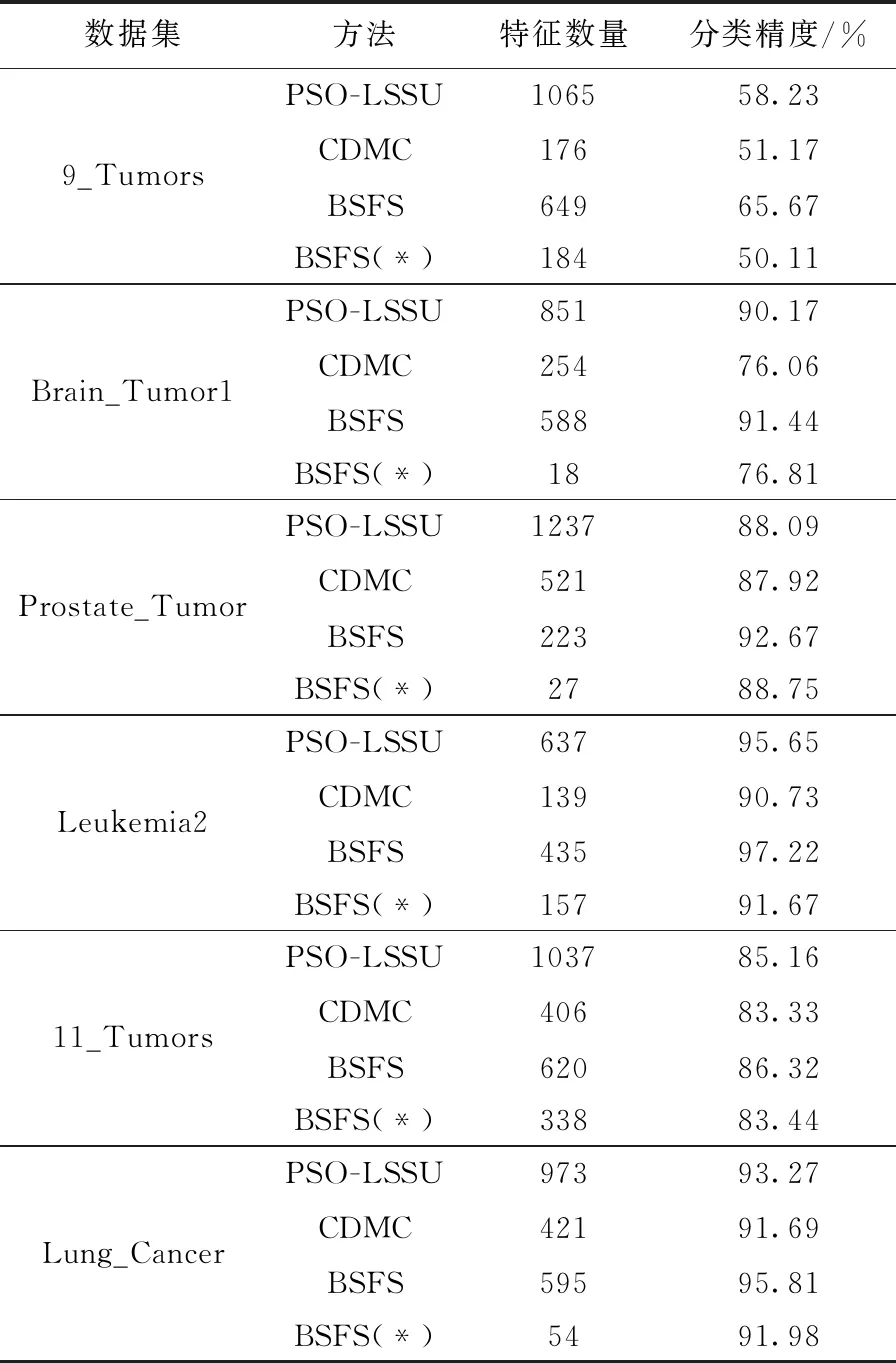
表6 BSFS与PSO-LSSU和CDMC的对比结果

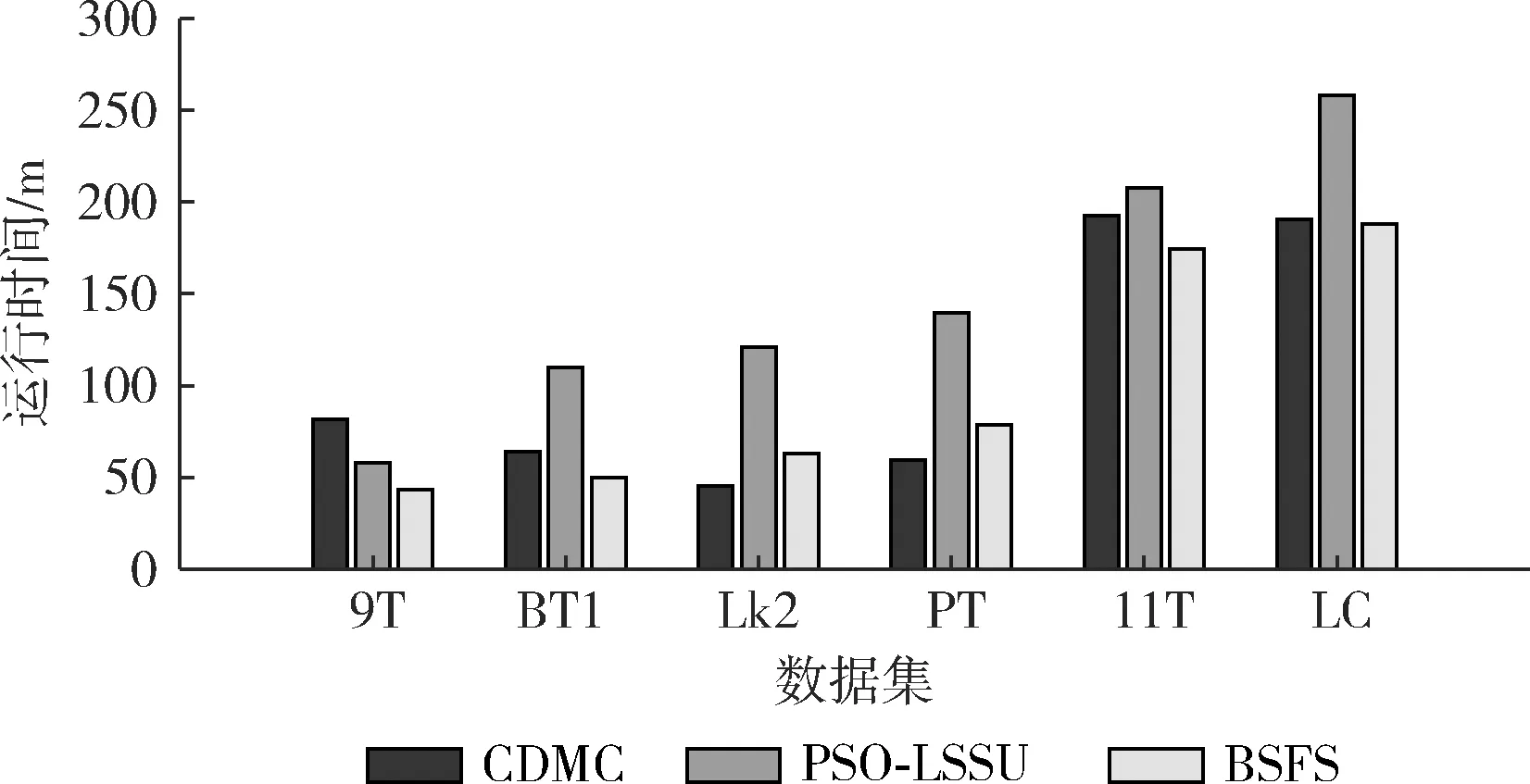
图4 3种方法运行时间对比