基于Bell态的量子隐私比较协议
郑 涛,张仕斌,李雪杨,邵婷婷
(成都信息工程大学 网络空间安全学院,四川 成都 610225)
0 引 言
1984年,Bennett和Brassard利用单光子的偏振态共同研发了世界上第一个量子密钥分发协议(quantum key distribution,QKD),即BB84协议。随后新的QKD协议及其相关的实验研究也不断出现[1,2]。为了满足不同的实际应用场景需求,人们提出了量子身份认证(quantum identity authentication,QIA)[3,4]、量子秘密共享(quantum secret sharing,QSS)[5-7]、量子安全直接通信(quantum secure direct communication,QSDC)[8-10]等一系列应用性量子密码协议[11-13]。隐私比较属于经典信息安全领域的“百万富翁”问题,即两个富翁想知道到底谁更有钱,但是都不愿意透露自己的财富。在现实生活中,有如下应用场景:假设两个诚实用户Alice和Bob分别拥有一条秘密信息。Alice和Bob都想同时获得对方的秘密信息,但双方都担忧对方在获得自己信息后,拒绝提供他的信息给自己,并且都不希望自己的秘密信息泄露给第三方。为了在量子通信网络中避免这种风险发生,学者们提出了一些基于量子理论的隐私比较协议,但是大都需要通信的某一方先公开部分秘密信息,才能完成隐私比较,而且协议过程中粒子的利用效率不高。
为了增强量子隐私比较过程的平等性,提高粒子传输效率,本文提出了一种基于稠密编码的量子隐私比较协议。通过安全性分析,证明了本协议在外部攻击、内部攻击等多种攻击策略下都是安全可靠且高效的。并且在隐私比较过程中,一比特的量子数目可以传输两比特的用户信息量。
1 基本原理
1.1 Bell态
单粒子量子态可以写成 |φ〉=α|0〉+β|1〉, 其中α和β分别为粒子坍缩成 |0〉态和 |1〉 态的概率值。且满足: |α|2+|β|2=1。 两粒子量子纠缠系统由A粒子序列与B粒子序列组成,可以由以下4个Bell态描述
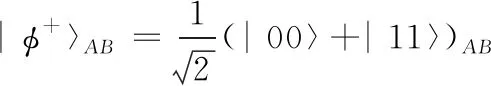
(1)
1.2 Pauli算符
在Hilbert空间中,存在线性算符(Pauli算符),用来改变量子矢量的状态。Pauli算符以Pauli矩阵为基础进行构造,4个基本的Pauli算符与Pauli矩阵定义如下
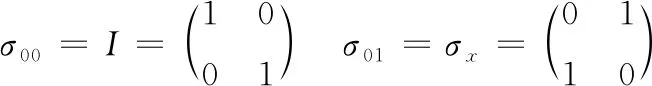
(2)
单粒子量子态 |φ〉=α|0〉+β|1〉 经过4种Pauli算符后变为
σ00|φ〉→|φ〉σ01|φ〉→β|0〉+α|1〉σ10|φ〉→eiπ/2(-β|0〉+α|1〉)σ11|φ〉→α|0〉-β|1〉
(3)
4种Bell态粒子经过Pauli算符操作后,也有类似的状态改变,以Bell态 |φ+〉AB为例,容易验证以下关系成立
σ00|φ+〉AB=|φ+〉ABσ01|φ+〉AB=|ψ+〉ABσ10|φ+〉AB=|φ-〉ABσ11|φ+〉AB=|ψ-〉AB
(4)
1.3 Bell纠缠
将N对Bell态 |φ+〉AB粒子解纠缠,形成 |A〉i和 |B〉i两个单粒子序列 (i=0,1…N)。 假设Alice对 |A〉i单粒子序列执行Pauli操作,Bob对 |B〉i单粒子序列执行Pauli操作;操作完成后Alice或Bob将 |A〉i和 |B〉i粒子序列按照它们的初始序列顺序再次纠缠,具体的操作步骤可以简要描述为:
Alice或Bob对 |A〉i和 |B〉i这两个单粒子序列,按照它们在Bell态 |φ+〉AB粒子的初始顺序,对其进行Bell态联合测量,使得 |A〉i和 |B〉i再次纠缠形成新的Bell态粒子。对解纠缠后的两个单粒子执行Pauli操作后,形成的Bell态粒子与Pauli操作之间的关系见表1。

表1 Puali操作与Bell态粒子的测量结果
2 协议描述
假设Alice拥有的秘密信息为X=(x0,x1…xn), Bob拥有的秘密信息为Y=(y0,y1…yn)。 且有xi,yi∈(0,1)。 双方秘密共享的信息编码规则如下
σ00→00,σ01→01,σ10→10,σ11→11
(5)
为了减少协议的复杂度,降低Bell态粒子在制备和纠缠,以及解纠缠等量子操作过程中的错误率,本文引入不可信第三方(untrusted third party,UTP)进行Bell态粒子的制备分发等操作。协议具体步骤如下:
(1)UTP制备N对Bell态粒子序列 |φ+〉AB, 然后UTP抽取粒子序列中所有下标为A的粒子组成单粒子序列P1, 抽取所有下标为B的粒子组成单粒子序列P2; 为了防止外部窃听,UTP在序列P1和P2中插入足量的诱骗粒子,并将P1通过量子信道发送给Alice,将P2发送给Bob。
(2)Alice和Bob按顺序接收完粒子序列后,分别通知UTP公布他们各自接收粒子序列中诱骗粒子的位置,以及诱骗粒子使用的测量基。Alice和Bob对各自的粒子序列进行窃听检测:双方根据UTP公布的位置信息,抽取出诱骗粒子,使用UTP公布的测量基进行测量并将结果公布。如果得到的测量结果错误率高于设定的阀值,说明粒子分发过程中有外部窃听,协议取消。否则,协议进行到下一步。
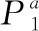
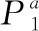
(5)UTP按照接收顺序,对完成窃听检测后的两个单粒子序列执行Bell联合测量,使其再次纠缠。并将得到的Bell态粒子序列结果公布。注意:得到的粒子状态应该为4种 Bell态粒子的集合 (|φ±〉AB和 |ψ±〉AB), 如果出现了其它的粒子状态,说明发生了外部窃听或协议参与者有不诚实行为,协议取消。否则,协议进行到下一步。
(6)Alice和Bob根据UTP公布的粒子态信息,结合自己对单粒子序列执行的Pauli操作,由表1和编码规则(5),双方可以同时推出对方完成的Pauli算符集,进而获得对方的秘密信息。Alice将自己的秘密信息X与推出的Bob秘密信息Y′进行异或,得到x=X⊕Y′, Bob同样操作得到y=Y⊕X′, 双方计算x=y是否成立,如果不成立,说明UTP公布了错误的贝尔态粒子状态或者参与方有不诚实行为,协议取消。反之,双方获取对方的秘密信息。
3 协议分析
3.1 协议的效率分析与正确性分析
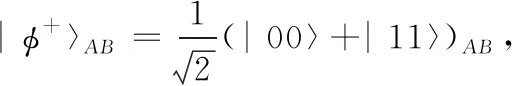
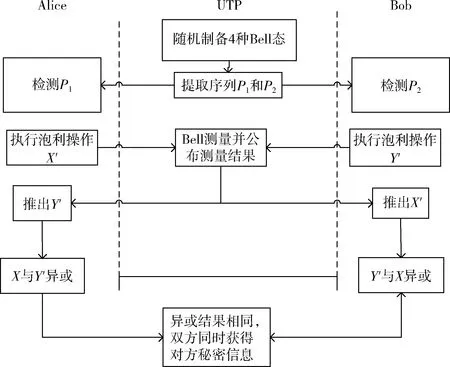
图1 协议简化流程
3.2 协议的安全性分析
通过分析协议步骤可以得知,协议面临来自通信参与方和UTP的内部攻击威胁,窃听者的外部攻击威胁。
3.2.1 对UTP的安全性分析
在本协议中,UTP需要完成的事情有:①制备并分发贝尔态粒子;②对Alice和Bob发回的粒子进行Bell联合测量,并公布正确测量结果。因此UTP可以通过公布虚假的测量结果(即假信号攻击)来试图获取Alice和Bob的秘密信息。但在本协议中,UTP将不会获得任何有用信息。首先,由于编码规则是由Alice和Bob秘密共享的,并且通信双方不会公布任何与秘密信息直接相关的内容,因此UTP不会获得任何直接的秘密信息。其次,如果UTP公布的是虚假的测量结果,Alice和Bob根据UTP公布的错误测量结果,通过表1和编码规则推出对方执行的泡利操作是错误的,但是此时UTP依然不会获得任何有用的秘密信息。如果通信双方在获取了对方的秘密信息后,将自己的秘密信息与推测出的对方秘密信息进行按位异或,并通过量子信道发送给对方,经过简单判断就可以发现UTP是否公布了错误的贝尔态粒子状态。例如:因此,UTP执行假信号攻击无法获得任何与用户秘密信息相关的内容。
3.2.2 对用户的安全性分析
假设Bob试图欺骗Alice,他在对粒子序列不按照秘密信息Y执行泡利操作。设Alice的秘密信息为11,Bob的秘密信息为10,他却对粒子执行σ00操作试图获取Alice的秘密信息。Alice对自己的粒子执行了正确的σ11操作后,双方将粒子发回给UTP。UTP完成Bell测量后公布粒子状态 |φ-〉AB(Bob如果执行了正确的σ10操作,UTP公布的粒子状态本应为 |ψ+〉AB), 此时Bob根据UTP公布的 |φ-〉AB和自己的秘密信息,根据表1推出Alice的秘密信息为“11”,但是Alice推出Bob的秘密信息为“00”。当双方在协议第(6)步验证时,x=y将不会成立,Alice发现Bob的不诚实行为,并且协议立即取消。因此Bob不能获得Alice全部的秘密信息。
3.2.3 截获/重发攻击
假设外部窃听者想通过截获/重发的攻击手段获取通信双方的秘密信息。分析协议可知,在UTP分发粒子过程,以及Alice与Bob发回粒子给UTP的过程中,步骤(2)和步骤(4)都会抽取诱骗粒子进行窃听检测,因此外部窃听者都会被检测出来。因此截获/重发攻击手段对本协议将不会有作用。
3.2.4 附加粒子纠缠攻击
假设Eve截获UTP发送给Alice的粒子序列P1, 附加了纠缠操作Ue后,附加粒子序列E与P1组合态形成的希尔伯特空间存在如下变换
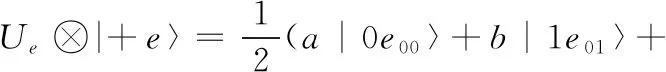
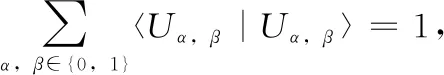
|a|2+|b|2=1 |a′|2+|b′|2=1ab*=(a′)*b′
根据上面的式子可以推出: |a|2=|a′|2, |b|2=|b′|2, 于是Eve通过附加粒子纠缠攻击,被检测出来的概率为p=|b|2=1-|a|2=|b′|2=1-|a′|2。 如果Eve想避免引入错误,则附加粒子与UTP制备的粒子构成的系统必定总是处于直积态;此时表明辅助粒子与UTP制备的Bell态之间没有任何关联。即Eve不能获得任何有用的信息。
4 结束语
本文提出一种基于贝尔态的量子隐私比较协议,可以实现通信双方平等的交换秘密信息。本协议可以防止一方欺骗另一方,从而获得其秘密信息,通信的双方通过第三方公布的消息同时获得对方的秘密信息。本协议通过引入不可信第三方,减小了协议的量子操作复杂度。同时可以抵御外部攻击,截获重发攻击,附加粒子纠缠攻击,以及用户的攻击,确保信息的安全可靠,平等高效的互换。

