基于特征选择的两级混合入侵检测方法
江泽涛,周谭盛子+,胡 硕,时 晨
(1.桂林电子科技大学 计算机与信息安全学院 广西图像图形处理智能处理高校重点实验室, 广西 桂林 541004;2.桂林电子科技大学 计算机与信息安全学院 广西可信软件重点 实验室,广西 桂林 541004;3.南昌航空大学 信息工程学院,江西 南昌 330063)
0 引 言
随着科学技术的发展,互联网已经渗透到人们生活及工作的各方面。网络的快速在提供便利的同时也诱发了一系列问题,如何保障用户数据信息的安全性成为当下亟待研究和解决的重点。入侵检测作为构成网络系统和主动防御体系的重要理论和手段而备受关注。
近年来,机器学习在入侵检测中得到了广泛的应用。闫義涵[1]为了克服传统的K-Means算法在很大程度上依赖于k值的问题,提出了一种改进的K-Means算法,通过层次聚类思想动态地确定k值,使用基于聚类中心位置变化的方法进行入侵检测。欧阳丽[2]针对当前随机森林算法在检测精度方面的不足,提出了基于果蝇优化的和聚类优化的随机森林算法,利用较少的基分类器改善了算法的精度。Guo等[3]将异常检测和误用检测进行级联,并引入了K近邻算法,能有效识别未知攻击类型,有效降低了算法的误报率。随着深度学习在图像处理方面的广泛应用,其有效性也越来越被入侵检测相关研究人员认可。张玉清等[4]总结了近年来深度学习在网络空间安全上的应用,并从分类算法、特征提取和学习效果等方面进行了分析,突出了深度学习在入侵检测技术应用上的问题与机遇。张思聪等[5]为了进一步提高检测准确率,提出了一种基于深度卷积神经网络(deep convolutional neural network,DCNN)的入侵检测方法,通过学习有效特征并结合Softmax分类器得到最终分类结果。此外,基于特征选择的算法的研究也越来越成熟。Akashdeep等[6]利用信息增益和相关性作为特征约简的依据,以人工神经网络(ANN)作为分类器,减少了训练时间。Nathan等[7]提出了非对称深度自编码器,对不含标签的数据采用无监督学习的方法获得了源数据中具有代表性的特征进而提高了入侵检测算法的分类精度。以上的成果虽然都在一定程度上取得了较好检测性能,但对未知类型的攻击检测仍然存在漏报情况。
针对上述情况,本文提出了一种以特征选择为基础的混合入侵检测方法。与其它方法相比,其创新之处在于:①结合Fisher分和超图属性提出了一种新的特征选择方法;②提出了一种改进的K-Means聚类方法,构建了一种新的两级混合入侵检测模型。实验结果表明,本文所提方法达到了更高的准确率和检测率,实现了更低的误报率。
1 相关知识
1.1 Fisher分
已有的很多入侵检测方法都有以下的不足之处:算法的性能受数据倾斜和分布的影响较大,同时在计算过程中会有很多冗余的特征维度,这都会增加算法的综合复杂度,同时也会使算法的检测性能受到了不同程度的影响。特征选择则是在所有原始维度范围对众多特征属性进行统一处理,在结果中筛选掉那些相关性不高的冗余特征,并在此基础上完成对原始数据的降维择优,择出对原始数据表征效果代表性最佳的最小特征子集[8]。特征选择可分为过滤式、包裹式和嵌入式3种。本文采用独立于分类器的过滤式特征选择方法,这类方法通常选择和类别相关度大的特征子集。过滤式特征选择方法常用于对原始数据的预处理,该类方法能够较好过滤非关键性特征,尽可能的保留相关性较高的主体结构特征,最终降低特征集属性的维度。Fisher分[9]被看作是过滤模式中一种重要概念,其主要处理目标是在最大化不同类别下的样本之间的距离的同时最小化同一种类别中的样本之间的距离,而Fisher分的计算取值则是计算两者的比值。由此可以得出特征的Fisher分值与特征的分类决策能力之间呈正相关的关系。以FSi表示第i维特征的Fisher分值,则Fisher分的计算公式如下所示
(1)

1.2 超 图
超图作为图论中的重要延伸概念,其相比其它类简单图模型,能够表征更加复杂的多元关系以及实体之间的复杂交互关系。在入侵检测方法中可以使用超图模型较好表示数据中各实体对象之间的所属关系[10]。对于超图H={V,E}, 其中,顶点V={v1,v2,…,vm}, 超边E={E1,E2,…,En}。 超图结构如图1所示。
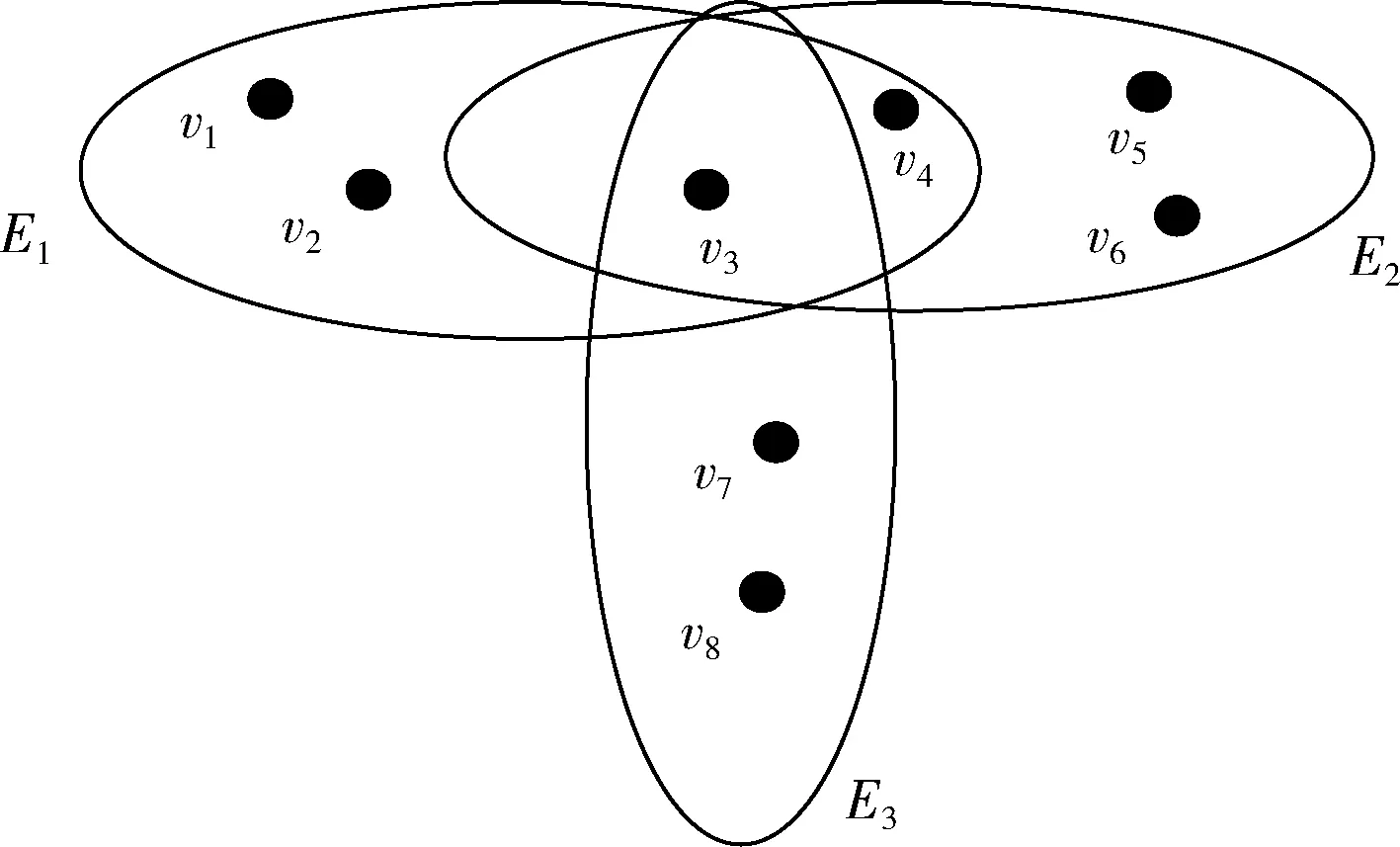
图1 超图结构
对于给定的一个超图H={V,E}, 若E={E1,E2,E3},V={v1,v2,v3,v4,v5,v6,v7,v8}, 其中E1={v1,v2,v3,v4},E2={v3,v4,v5,v6},E3={v3,v7,v8}, 则超边E1与E2的交集为 {v3,v4}, 超边E1、E2与E3的交集为 {v3}。 若一个超图H存在Helly属性,其中,H={V,E}, 顶点V={v1,v2,…,vm}, 超边E={E1,E2,…,En}, 则需要满足Ei∩Ej≠∅(i≠j且i,j∈n), 如图2所示。
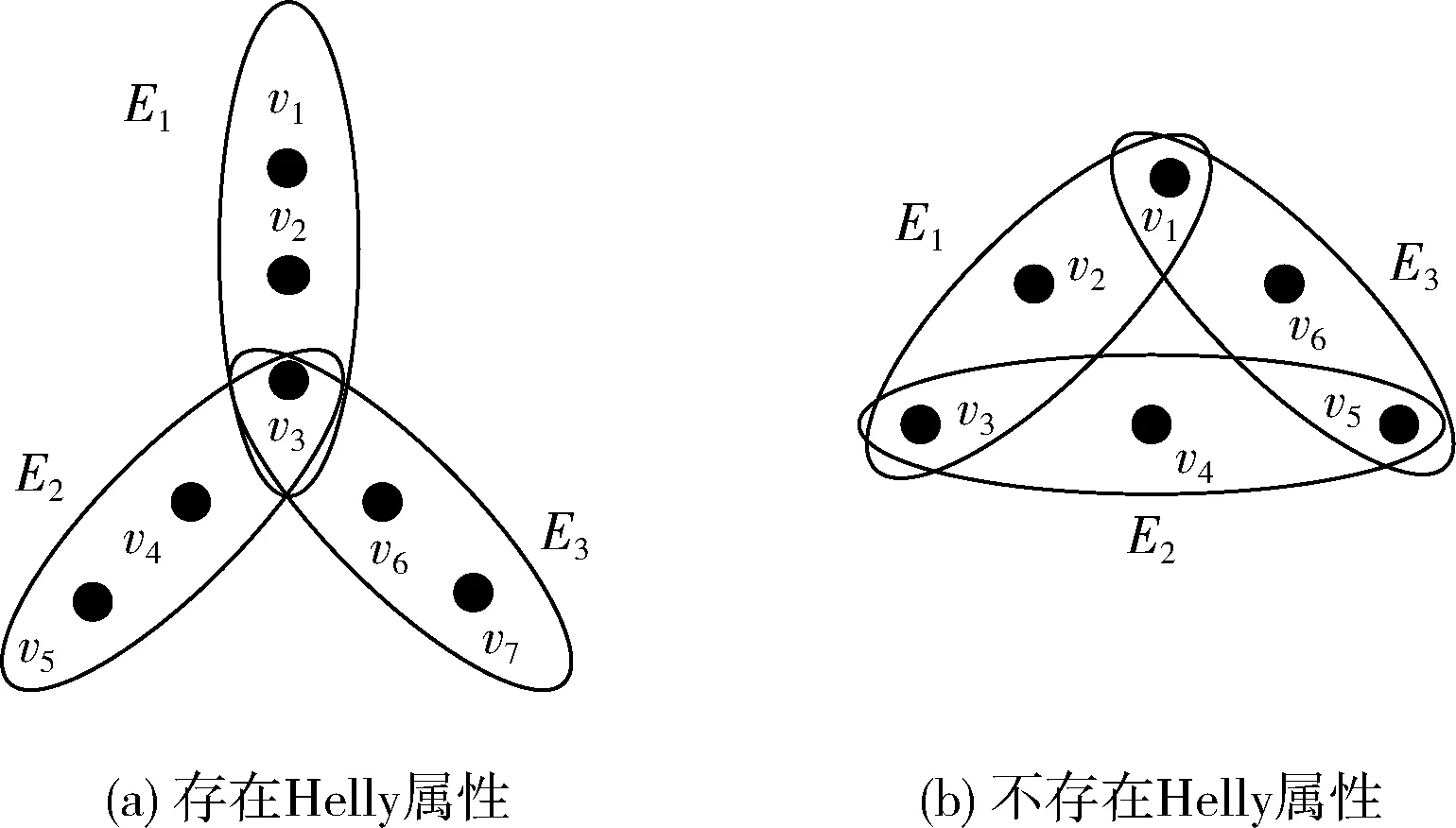
图2 超图Helly属性
图2(a)表示任意一对超边都有相同的交集,在超图H={V,E} 中,E={E1,E2,E3},V={v1,v2,v3,v4,v5,v6,v7},E1={v1,v2,v3},E2={v3,v4,v5},E3={v3,v6,v7}, 利用Helly属性可以得到顶点v3是超边 {E1,E2,E3} 的共同交点,即E1∩E2={v3},E1∩E3={v3},E2∩E3={v3}。
图2(b)是含三角形的超图,在超图H={V,E},E={E1,E2,E3},V={v1,v2,v3,v4,v5,v6},E1={v1,v2,v3},E2={v3,v4,v5},E3={v1,v5,v6},E1∩E2={v3},E1∩E3={v1},E2∩E3={v5}, 即 {v3}∩{v1}∩{v5}=∅。如果图中任意一对超边之间不存在任何相同交集,则此图不具有Helly属性。
1.3 随机森林算法
随机森林是由多棵树型分类器组成的集合,最终分类结果由基础树型分类器投票产生,其基础树型分类器通常采用没有剪枝的CART决策树。本文采用基于信息增益的随机森林算法。在过滤式特征选择方法中使用基于信息增益理论的方法度量每一个特征维度对检测分类的贡献度大小,将贡献度较低的特征作为冗余特征去除掉。与之相对应的是,误分类的概率与特征的信息增益之间是一个朴素的负相关关系。
样本S的熵可通过下列公式计算
(2)
其中,S为数据集,K为类别数,Si为第k类样本数, |S| 为总样本数。
特征属性A对数据集S的条件熵公式如下所示
(3)
对S进行划分,得到n个子集,划分依据为A的取值,划分后的样本子集为S1,S2,…,Sn, |Si| 为第i个子集Si的样本数, |S| 为总样本数,K为类别数, |Sik|为子集Si中类Ck的样本数。
特征属性A的信息增益公式如下所示
IG(A)=H(S)-H(S|A)
(4)
基于信息增益的随机森林的算法主要分为6个主要步骤:
(1)对包含K个决策树的随机森林中的每一棵决策树进行n次有放回的随机抽取,得到的抽取样本记为D={(x1,y1),(x2,y2),…,(xn,yn)},xi表示第i个样本的特征集,yi表示第i个样本的所属类,随后从n个样本对中随机选取j个样本构成特征子集A(a1,a2,…,aj);
(2)对决策树中样本进行多轮分类,如果分类结果相同就结束此轮分类计算,并将当前分类结果作为此次分类的最终类别,否则执行步骤(3);
(3)采用信息增益最大的属性进行划分,信息增益最大的属性记为ai, 随后将ai从特征子集A中删除;
(4)对每个子节点分别执行步骤(2)并循环重复当前步骤;
(5)若全部特征属性都用于划分时,最后节点处的样本属于不同的类别,则此时当前节点的类别为该节点中的数量最多的类别;
(6)在测试阶段,利用K棵决策树分别对样本进行分类,样本的最终类别由所有决策树投票决定。
由式(2)~式(4)可知,通过对样本特征属性的信息增益进行计算和筛选,决策树能很好的区分属于正常操作类别的数据和部分属于非法攻击操作数据,因此,基于信息增益的随机森林算法对攻击数据检测率较高,但是此类方式的误报率也处于较高水平,本文设计级联分类器体系,并将此方法作为第一级分类器组件,期望能够提高对部分异常数据的检测率。
1.4 K均值(K-Means)算法
K-Means算法是典型的基于划分的聚类方法,其目的在于将数据集划分为若干个子集且分别代表一个类别。其核心步骤是对每个点计算到各个预定义的已知类别的中心位置的欧氏距离,并将此距离结果作为划分其所属类别的依据,并同步更新所属类别的中心位置,重复上述步骤直至中心收敛为止。其中,两个n维样本xi与yj之间的欧式距离公式如下所示
(5)
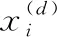
(6)
其中, |Ck| 为第k类簇类的样本数,xi为Ck中的样本。
为了克服传统K-Means算法初始聚类中心k值选取的随机性,本文采用基于密集度的K-Means++算法,与传统的K-Means++不同的之处在于:该方法引入了密度阈值的概念,以此来避免K-Means++算法在选取初始中心位置时的随机现象,这样就可以在决策初始聚类中心时受到更少来自部分离群孤立数据点的不利影响。
基于密集度的K-Means++算法的具体步骤如下:
(1)输入聚类数k距离阈值ε和密集度阈值α;
(2)根据式(5)的定义计算k个距离较远的样本与其附近的α个不同样本数据点之间的距离,如果能够满足d(xi,xj)≤ε, 则可将所选取的k个样本作为初始中心位置,否则的话重复上述操作选取更远的另外k个样本。直到找到的k个样本能够满足步骤(2)中介绍的式子;
(3)计算每个样本到各个簇类中心的位置的欧氏距离并选择距离最近的簇类,当前样本随后加入到此簇类中去,更新簇类中心位置;
(4)分类过程终止的条件是聚类中心趋于稳定,其它情况则重复流程(3)的操作。
聚类算法大都是以距离计算为核心思想的分类方法,其中基于密集度的K-Means++方法在入侵检测问题中能够有效将剩下的攻击数据和正常数据分类到不同的簇类中去,从而就能够提高分类器的全局检测率且降低误报率。
2 基于特征选择的两级混合入侵检测方法
2.1 基于超图的特征选择方法
互联网的迅速发展使得信息的存储和处理变得异常困难,近年来,机器学习方法的注入为入侵检测技术带来了新的生命力,但是大数据的数据结构和数据类型更加多元和复杂,从而使得对数据的处理也更加复杂,而基于特征选择思想的理论和方法就是想要从大量复杂冗余的海量数据中提取出具有更多实际意义的业务信息。通过删除一些冗余和不相关的特征属性选择出最小特征子集用于表征原始数据。本文根据特征属性对类别的区分程度,生成最小特征子集,从而实现特征择优。利用Fisher分值可以从数值上直观准确地对比不同的特征维度对分类能力的影响。另外,由于本文对入侵检测数据集进行五分类研究,所以引入超图着重分析满足Helly属性的特征。本文提出的方法,主要包括3个步骤:①对原训练数据中的各个特征进行Fisher分值计算,并筛选掉对数据分类的影响不明显的特征属性;②将特征与样本的关系用超图表示;③最优特征子集的选择则使用超图中的Helly属性进行处理。数据中的类别对应超边,数据特征对应超图中的顶点。其算法流程为如下所述:
输入:S={S1,S2,…,Sn} /*训练集中的n个样本*/
F={FS1,FS2,…,FSl} /*训练集中的样本特征,l表示特征维数*/
C={C1,C2,…,Ck} /*训练集中的k个类别*/
输出:f={f1,f2,…,fm} /*特征子集维度m*/
Begin
{
for j=2 to k
{
for i=1 tol
//求每一维特征的Fisher分值
descend order (FSi)
//降序排列Fisher分值
for i=1 to 20
Cj={FSi} //取前20个特征
}
ifCi∩Cj=FSq(i,j∈k,i≠j) //利用超图的Helly属性选择最优特征子集
f={FSq}
}
End
2.2 基于特征选择的两级混合入侵检测方法
基于信息增益的随机森林算法分析了各个特征属性对最终分类结果的影响,而基于密集度的K-Means++算法则是从密集度和距离两个层面考虑,方法整个过程划分为两个不同级别的分类器,其中第一级分类器在对攻击数据的识别上有较高准确率,所以其能够以很高的准确率识别部分攻击样本。第二级分类器以改进的K-Means算法为基础对第一级分类器无法准确分类的剩下数据进行第二级分类,此方法能够在提高对入侵数据的检测率的同时很好控制对正常数据的误报概率值。具体步骤如下:特征择优阶段:①首先在训练阶段计算训练数据集各个类别中每一维特征的Fisher分值并按降序排列;②其次在各个类别中选择Fisher分值排在前20的特征并添加到特征子集FSsub中;③最后对FSsub进行复筛,对具备Helly属性的特征添加到最优特征子集f中;检测阶段:①先以随机森林作为第一级分类器,这一级的分类结果得出的攻击样本直接作为最终的分类结果;②以基于密集度的K-Means++算法作为第二级分类器,其处理对象是第一级分类器中无法准确分类为攻击样本的剩余数据,得到的分类结果将作为最终的检测结果。结合第一级分类器的部分分类结果,得到最终的全部分类结果。图3表示的是此文提出的级联分类器的算法流程图。对本文算法的实验结果的描述和分析将会在第3节作详细描述,最终实验结果表明本文的算法的性能要比仅仅采用随机森林分类模型或K-Means算法的单一分类检测模型要好。
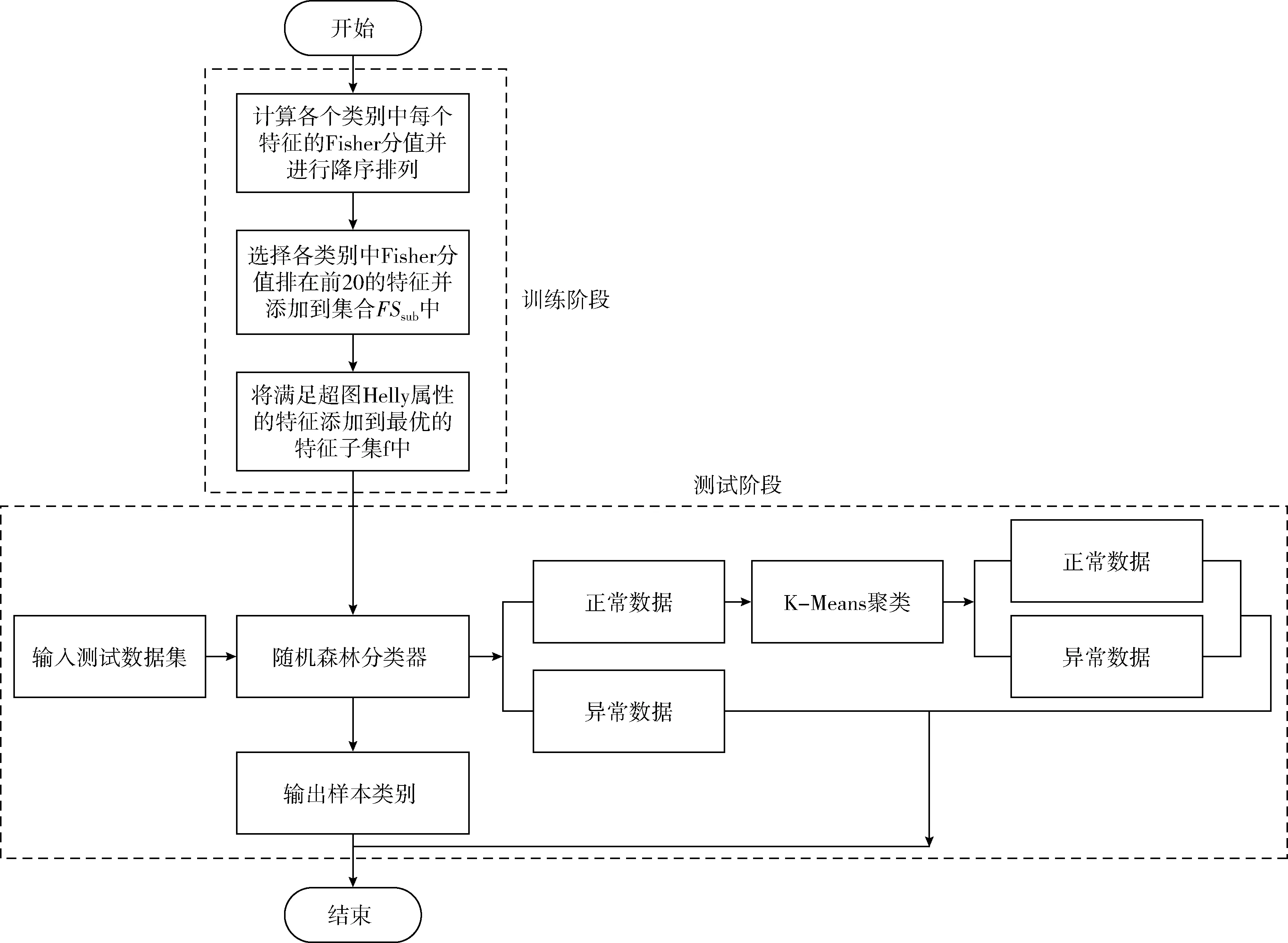
图3 基于特征选择的两级混合入侵检测算法流程
3 实验与分析
3.1 实验设置
3.1.1 实验数据
KDD CUP’99数据集来自麻省理工学院林肯实验室,在业内目前被广泛用于对入侵检测问题研究[11]。该数据集中的每个样本有42个维度的特征数据。属性分类及个数参见文献[12]中表2-1。该数据集主要包括4种类型的攻击:Dos(拒绝服务攻击)、Probe(端口监视或扫描)、R2L(远程主机的未授权访问)及U2R(未授权的本地超级用户特权访问)。本文采用10%的KDD CUP’99数据集作为训练集,该数据集包含了494 021条数据记录,其攻击类型参见文献[12]中表2-2。为了检验模型的泛化性能,采用KDD CUP’99 Corrected数据集作为测试集,该数据集包含了311 029条数据记录,其中包括了17种新型攻击类型,详情参见文献[12]中表2-3。各类别在训练集和测试集中的数目参见文献[12]中表2-4。
3.1.2 数据预处理
KDD CUP’99数据集中每条连接记录的41个特征属性有38个数字型特征属性和3个字符型特征属性构成,数据预处理阶段主要是对原数据中的字符型数据进行数值化转换,随后对每个维度的数据进行数学上的归一化处理,所采用的归一化算法如式(7)所示
(7)
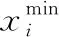
3.2 实验结果与分析
一个好的入侵检测系统是能够在检测率和误报率之间达到很好的权衡的。因此,本文选取了准确率(accuracy,ACC)、精确率(precision,PRE)、检测率(detection rate,DR)、误报率(false alarm rate,FAR)4个指标用于衡量算法的性能。计算公式如下所示
(8)
(9)
(10)
(11)
其中,TP为正确识别的正样本数,FP为错误识别的正样本数,TN为正确识别的负样本数,FN为错误识别的负样本数。
将本文提出的入侵检测模型与现有的分类模型在准确率和精确率上进行比较,实验结果见表1。
由表1可以看出随机森林算法对检测数据中的真实攻击类型的检测准确率都很稳定,但是在全面性上有明显的不足,但是在正常样本和U2R攻击类型的精确率有明显的不足,经分析这其中的根本原因在于该算法对这两个特定类型样本的识别率较低;朴素贝叶斯算法在正常样本及各类攻击中性能都不突出;支持向量机算法对Dos和U2L类攻击的检测性能尤为突出;K-Means算法全局结果与其它算法相比都有明显差距,这种结果产生的原因在于K-Means 方法受聚类中心选取的随机性的影响较大。文献[14]以算术残差法及超图得到的特征子集为基础,并用概率神经网络对样本进行分类,结果表明其对正常样本及Dos类攻击的检测准确率较优。本文提出的入侵检测模型通过删除冗余特征得到对原始数据特征表征效果较好的最小特征子集,使用基于信息增益的随机森林算法进行分类过滤,能够准确过滤出部分真实异常的数据,但是我们发现测试数据集当中存在一些属于新出现类型的攻击数据,对于这种情况下数据,仅仅依靠随机森林算法的分类器的结果漏报率会比较高,基于对此种情况改进的考虑,使用基于密集度概念的K-Means++算法进行二级分类,实验结果表明,本文提出的级联后的分类器在保证很高的检测准确率的同时,对正常样本的检测精度也有了很大的提升。
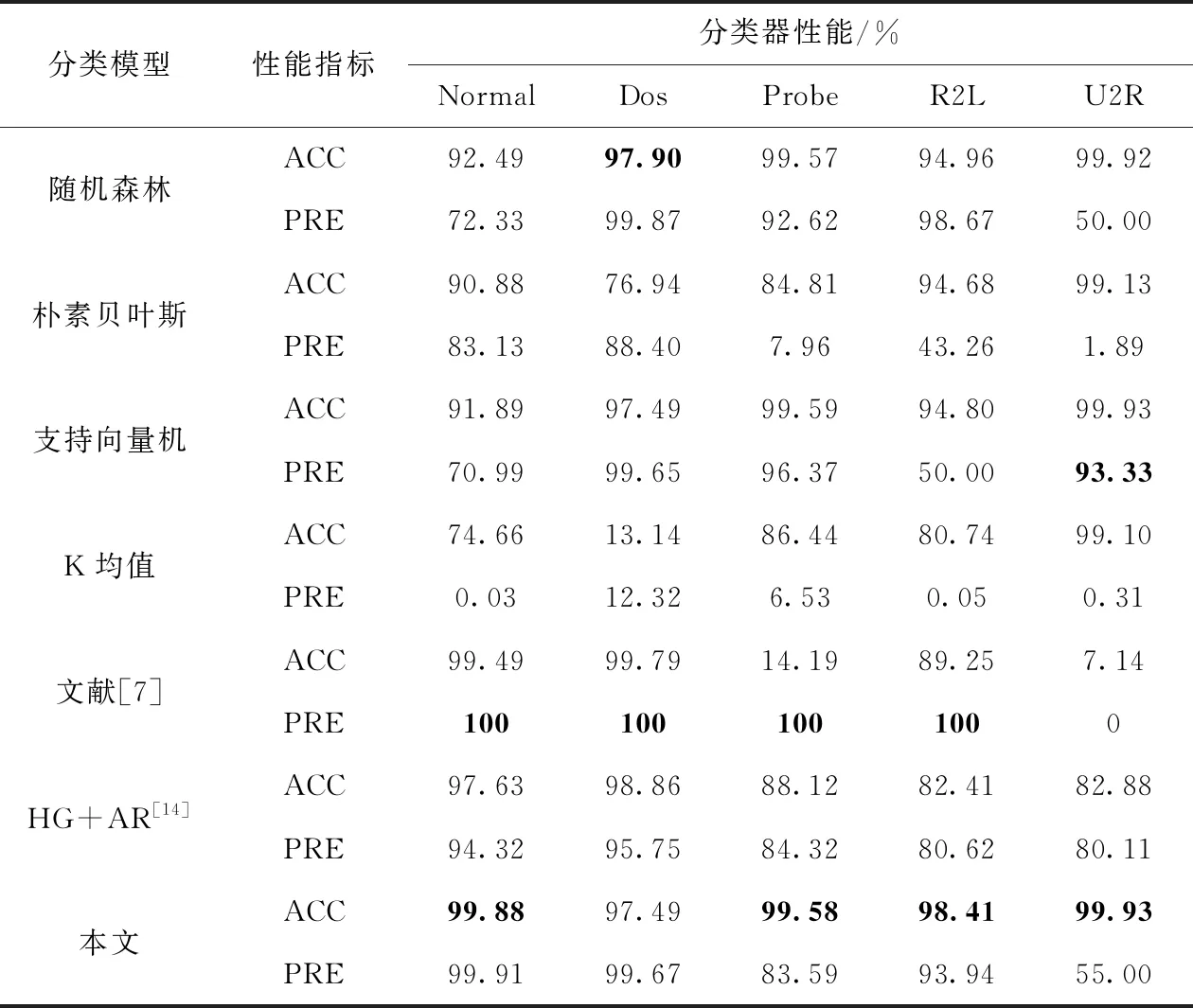
表1 分类器性能对比(一)
就检测率和误报率方面,将本文提出的入侵检测方法与其它方法进行比较,实验结果见表2。

表2 分类器性能对比(二)
由表2可以看出Guo等[3]选取KNN作为分类器,先对测试集进行异常检测,然后分别利用异常检测和误用检测对攻击样本和正常样本进行检测,其实验结果表明该方法的检测准确率不是很好。张思聪等[5]提出的DCNN方法在检测率指标和误报率指标上都能够达到较为均衡的全局稳定性。Nathan等[7]利用非对称深度自编码器进行入侵检测问题研究,其算法结果的检测率有较好的表现,但是误报率方面存在明显的缺陷。Kuang等[13]利用核主成分分析进行特征降维,采用多级支持向量机作为分类器,并使用遗传算法的思想理念进行参数的策略优化,除了算法复杂度得到改善以外,其计算结果表明该模型的分类综合性能明显优于传统的支持向量机算法。Raman等[14]在特征选择思想的基础上,引入概率神经网络对样本进行分类,结果表明该模型并未在检测率和误报率之间达到很好的平衡。本文在基于Fisher分和超图的Helly属性的特征选择基础上,先后利用随机森林算法和K-Means聚类进行分类可以达到更高的检测率和更低的误报率,优于现有的入侵检测方法。
4 结束语
本文提出了一种基于特征选择的两级混合的入侵检测方法。为了有效降低算法的训练时间,引入了特征选择,先计算各类别攻击的Fisher分值,再利用超图的Helly属性确定最优特征子集。先用随机森林作为第一阶段的分类器,对测试集进行预测,随后用改进的K-Means作为第二阶段的分类器,针对第一阶段预测得到的正常样本进行二次检测。结果表明,本文提出的方法在准确率、检测率及误报率方面均好于其它模型,是一种可行的入侵检测方法。

