结构动态可靠性分析的最大熵方法

赵恩康，李洪双

(南京航空航天大学 航空宇航学院，江苏 南京 210016)

0 引言

结构动态可靠性分析的任务是量化计算一个结构或结构系统在工作了一定的时间t或者时段[0,t]后的可靠度。尽管针对结构动态可靠性分析已经有了许多研究工作，但是兼顾高精度和高效率仍然是一个挑战。传统的蒙特卡洛法(monte carlo simulation, MCS)可以用于结构动态可靠性分析，但在实际应用中由于需要大量抽样计算，所需的计算成本太高，阻碍了它在实际工程中的应用。现有的方差缩减技术同样面临大计算量困难，例如重要抽样法[1]。因此结构动态可靠性分析领域目前主要采取近似方法，主要包括首次超越法[2-3]和极值法[4-6]。首次超越法认为极限状态函数超过安全阈值的上界或低于其下界，结构就会发生失效。通过假设不同“超越事件”之间是相互独立的，结构动态可靠度就可以通过在时间域上对穿越率进行积分来获得。大多数首次超越法的局限性在于忽略了超越时间之间的相关性及线性近似带来的误差。极值法的基本思想是考虑极限状态函数在目标时段内的极值，如果极值大于给定的阈值，则结构发生失效。目前，基于极值思想已经发展出多种结构动态可靠性分析方法，例如，WANG提出了一种嵌套极值响应面法[6]，DU和HU提出了一种混合高效全局优化法[7]，CHEN和WANG则提出了一种自适应极值响应面法[8]。但是现有极值法的性能依赖于代理模型对极限状态函数的逼近精度和范围。若不能高精度地拟合结构极限状态函数及其极值，相应的动态可靠性分析结果是不可信的。

本文基于极值思想，提出一种结构动态可靠性分析的最大熵方法，可以直接处理一般形式的动态极限状态函数。首先采用拓展最优线性估计(expansion optimal linear estimation, EOLE))[9]方法，将极限状态函数中的输入随机过程离散化为一系列随机变量之和的形式。对所研究结构进行结构分析，计算得出目标时间区间内极限状态函数的极值；进而利用极值的前四阶统计矩和最大熵原理拟合极值分布。基于最大熵分布，求解结构动态可靠度。文中利用工程算例验证了所提方法的有效性。

1 结构动态可靠性分析

1.1 动态可靠性定义

结构动态可靠性分析的极限状态函数的一般形式为

g(X,Y(t),t)

(1)

其中X=[X1,X2,…,Xn] 是n个输入随机变量的向量；Y(t)=[Y1(t),Y2(t),…,Ym(t)] 是m个与时间有关的输入随机过程。如果在时间区间[t1,t2] 内存在某一时间节点t，极限状态函数值超出安全阈值b，结构发生失效，即有

∃t∈[t1,t2],g(X,Y(t),t)>b

(2)

结构失效概率可以定义为

Pf(t1,t2)=Pr(g(X,Y(t),t)>b,∃t∈[t1,t2])

(3)

相应的动态可靠度为

R(t1,t2)=1-Pf(t1,t2)

(4)

由于极限状态函数的复杂性以及时间参数的存在，得到式(3)的解析解是非常困难的。蒙特卡洛法能够得到精确的结果，但由于需要大量样本来评估极限状态函数，计算成本极高。因此本文研究基于极值思想的方法。

1.2 极值法原理

极值法关注极限状态函数一段时间内的极值函数或者极值分布。那么基于极值思想，式(3)中的结构失效概率可以表示为

Pf(t1,t2)=Pr(gmax>b)

(5)

显然，式(5)中不含有时间参数，这就将时变问题转化为时不变问题。但是由于极限状态函数的复杂性，在实际工程中解析地得到其极值往往非常困难，所以目前已有研究工作主要是使用代理模型方法和近似方法得到结构响应的极值或者极值分布。

2 动态可靠性分析的最大熵方法

2.1 所提方法

为了解决现有方法的一些缺点，基于最大熵原理，本文提出一种新的结构动态可靠性分析方法。该方法的实施步骤如下：

1) 采用EOLE方法对输入随机过程进行离散化；

2) 采用拉丁质心Voronoi网格抽样生成高质量抽样样本；

3) 计算每条样本轨迹的极值，得到响应极值的样本；

4) 计算极值的前四阶矩，分别是均值、标准差、偏度和峰度；

5) 由极值的前四阶矩计算Lagrange乘子，然后拟合极值的最大熵分布；

6) 计算动态可靠度。

本文提出的动态可靠性分析的最大熵方法流程如图1所示。

图1 最大熵方法流程图

如图2所示，阴影部分的面积即为结构失效概率。

图2 极值分布计算失效概率示意图

下面针对步骤中关键理论和技术进行详细讨论。

2.2 随机过程的离散

在实际工程应用中，许多结构参数都具有不确定性，例如材料属性。大多数情况下，这种不确定性都可以通过随机变量来表征。但是仍然有一些参数随结构服役时间的累积呈现出时变随机特性，例如结构上的随机载荷，需要用随机过程来表征。若想对随机过程Y(t)进行抽样计算，在此之前需要对该随机过程Y(t)进行离散化处理。本文讨论的随机过程限定为高斯随机过程，该过程的均值函数、标准差函数和自相关系数函数分别为μY(t)、σY(t) 和ρY(t1,t2)。非高斯随机过程可以通过转换方法转化为高斯随机过程。

EOLE方法首先将时间[0,T]离散成s个离散时间点ti,i=1,2,…,s。考虑到计算上的简便，时间步Δt一般取定值。在时间点处多维随机变量的相关矩阵可以表示为

(6)

(7)

式中：Ui为相互独立的标准正态随机变量；ρY(t)=ρY(t,ti),i=1,2,…,s。

式(7)表明：在每一个时间点ti处，随机过程Y(ti)可以表示为一组标准正态随机变量Ui的线性和。基于以上结论，结构动态可靠性的极限状态函数可以转化为g(X,Y(t),t)=g(X,U,t) ，使得极限状态函数中不再隐式含有时间参数t。

2.3 拉丁质心Voronoi网格抽样

抽样样本点的质量会影响拟合的精度。目前常用的拉丁超立方抽样(latin hypercube sampling, LHS)是一种全空间非重叠填充的随机抽样方法，能够兼顾可行域与不可行域，但难以保证抽样的空间均匀性；BURKARDT[10]基于Voronoi网格提出了质心Voronoi网格抽样方法 (centroidal voronoi tessellation, CVT)。它将整个抽样空间划分为指定数目的Voronoi区域，Voronoi区域的质心即为抽样样本点，具有均匀性与稳定性的特点。

ROMERO[11]等人结合LHS方法和CVT抽样方法，提出了一种新的抽样方法，称为拉丁质心Voronoi网格(‘latinized’ centroidal voronoi tessellation，LCVT)抽样方法。对质心Voronoi网格进行特殊处理，使其具有拉丁超立方体的性质，此处理过程称为拉丁化。拉丁质心Voronoi网格抽样的具体实施步骤如下：

(8)

式中Uji表示在第j维空间内均匀分布的随机数。

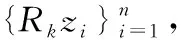
(9)

对质心Voronoi网格进行拉丁化，获得的新网格称为拉丁质心Voronoi网格。LCVT抽样方法兼具CVT方法的均匀性与LHS方法一定的随机性，能更好地反映出随机变量在设计空间的分布情况。

基于极值思想的结构动态可靠性分析方法的关键步骤是准确地计算极限状态函数g(X,Y(t),t)的极值。获得高质量抽样点后，带入结构分析模型，计算每个抽样点对应的轨迹，并获得结构响应在感兴趣时段内的极值。进一步计算结构响应极值的前四阶统计矩，为拟合最大熵分布提供约束条件。

2.4 最大熵分布

1948年，SHANNON[12]将热力学熵的概念引入到信息科学中，来定量描述一个随机事件的不确定性或信息量。基于信息熵的概念，JAYNE[13]在1957年提出了最大熵原理。最大熵原理可以表述为：在所有满足给定的约束条件的概率密度函数中, 使信息熵最大的概率密度函数就是最佳，即偏差最小的概率密度函数。

若X为连续型随机变量，其概率密度函数为f(x)，则其信息熵HX可定义为

(10)

根据最大熵原理，应该求使信息熵HX最大的概率密度函数f(x)。通常将随机变量的前n阶原点矩μi(i=1,…,n)作为约束条件，相应的优化问题为：

(11)

式(11)是一个等式约束极值问题，可以用拉格朗日乘数法求解，经过简单推导，可以得到最大熵分布

(12)

式中λi(i=1,…,n)为Lagrange乘子。根据概率密度函数的数学定义，求得标准化因子：

在估计最大熵分布时，随着使用的统计矩μi阶次增大，对样本中的信息利用也更加充分，最大熵分布拟合的精度也会提高。文中采用极值数据的前四阶矩作为约束条件拟合极值分布，它们分别是均值、标准差、偏度和峰度。

由于本文中使用了结构响应极值的前四阶矩拟合最大熵分布，无法获得最大熵分布的显示解，此时需要采用诸如标准牛顿法[14]的数值算法求解Lagrange乘子。但是标准牛顿法需要求解n个带有积分的等式，过程繁琐，计算量大，效率较低，因此文献中使用一种无约束最小化方法求解Lagrange乘子，基本过程如下：

定义一个以λi(i=1,…,n)为自变量的势函数Q(λ1,…,λn)

(13)

势函数Q(λ1,…,λn)对自变量λi的梯度为：

(14)

基于式(14)，进一步计算Q(λ1,…,λn) 的Hessian矩阵元素：

(15)

3 算例分析

水动力涡轮机可以将水的动能转化为叶片的转动机械能。此算例为时变河流载荷下的水动力涡轮叶片[18]。涡轮叶片的简化横截面如图3所示。

图3 涡轮叶片根部横截面

为了表征河流流速的时变特性，河流流速采用一个高斯随机过程v(t)表示，其均值μv(t)、标准差σv(t)和自相关函数ρv(t1,t2)分别为：

(16)

(17)

ρv(t1,t2)=cos(2π(t2-t1))

(18)

式中系数a、b和c的值如下：

在河流流速v(t)作用下，叶片根部的弯矩可以表征为

(19)

式中：ρ=1×103kg/m3为水的密度；Cm=0.3422为力矩系数。

该叶片的极限状态函数定义为

(20)

(21)

表1 涡轮叶片中随机变量

在[0,12]个月区间上计算涡轮叶片的失效概率，通过LCVT方法生成500条样本曲线，并与样本数目为106的MCS计算结果进行对比，失效概率结果如表2和图4所示，[0,12]个月区间极值的概率密度函数曲线如图5所示。

表2 涡轮叶片失效概率

图4 涡轮叶片失效概率

图5 [0,12]个月极值概率密度函数曲线

由表2和图4可知：随着时间的推移，涡轮叶片的失效概率逐渐增大，从第7个月开始保持不变，这是由于极限状态函数的极值落在[6,7]个月之间。在整个时间区间内，最大熵方法的计算结果都和MCS计算结果十分接近，并且相比MCS需要106次抽样，最大熵方法只需要500条样本曲线，说明最大熵方法兼具较好的计算精度和计算效率。

4 结语

本文基于极值思想，提出了一种结构动态可靠性分析的最大熵方法，能够处理形如g(X,Y(t),t)的一般形式的动态可靠性极限状态函数。该方法首先将随机过程离散为一组随机变量，再对极限状态函数中的随机变量进行抽样并计算样本点处的极值，最后通过样本极值数据利用最大熵原理拟合极值分布并计算动态可靠度。从文中算例的计算结果可以看出：该方法在精度上接近蒙特卡洛方法且兼具较高计算效率，有一定的工程应用价值。