γ转捩模型的分离修正及其应用研究

舒杰，仲冬冬，葛宁，杨荣菲

(南京航空航天大学 能源与动力学院，江苏 南京 210016)

0 引言

随着航空发动机的不断发展，对作为功率输出的关键部件低压涡轮的要求越来越高，而在高空巡航时，低压涡轮部件工作雷诺数处于各旋转部件中最低状态。低雷诺数条件下边界层往往处于层流，从而增加了其在逆压力梯度作用下分离的可能性，导致发动机性能的恶化[1]。有研究表明，高空条件下，低压涡轮部件效率降低1%使得耗油率增加0.9%[2]，而对于小型军用发动机巡航状态低压涡轮效率可能降低7%(与地面起飞状态相比)[3]。因此，多级低压涡轮低雷诺数效应受到广泛关注，深入理解边界层的转捩过程是高负荷低压涡轮设计的关键之一[4]。

为了准确预测低压涡轮中的边界层转捩现象，工程上普遍采用转捩模型与湍流模型耦合模拟的方法。WALTERS等[5]提出kT-kL-ω转捩模型，将雷诺应力与层流湍动能及湍流湍动能关联；DARIUS等[6]将该模型应用于三级低压涡轮流场分析，并与SA模型计算结果作对比，发现两种模型下叶片分离区的位置及尺寸存在显著区别。MENTER等[7]在k-ωSST模型上增加γ-Reθ两个输运方程，用间歇因子γ模拟层流向湍流转捩过程中边界层的间歇特性，具有完全当地化也不影响全湍流区的预测等特点；SHENG[8]将该转捩模型应用到SA模型上，同时提出SA模型上预测湍流度的方法；但γ-Reθ不具有伽利略不变性，对于运动壁面需要进行特殊处理，MENTER[9]等根据试验数据重新得到Reθc经验关系式，提出一方程γ转捩模型。模型适用于研究叶轮机械中转捩现象，形式较为简单；但在研究中发现，MENTER原始的γ模型在预测叶型开式分离时与试验值存在较大偏差，且关于模型在多级低压涡轮中的应用研究十分有限。

本文首先在MENTER提出的γ转捩模型基础上添加分离修正模型，并在T106D-EIZ叶栅低雷诺数工况下进行数值验证；然后，将带分离修正的γ模型应用于GE-E3五级低压涡轮，与未加转捩的SST模型计算结果对比分析；最后，研究了低雷诺数工况下GE-E3LPT流动损失特性，为低雷诺数下多级涡轮设计提供参考和借鉴。

1 数值方法

1.1 γ转捩模型及分离修正

本文的数值模拟采用课题组自主开发的CFD软件NUAA-Turbo中的RANS模块[10]，采用有限体积法，其中无粘对流通量采用Roe分裂法，粘性扩散项为二阶中心差分格式；湍流模型为k-ωSST模型，转捩模型为γ模型。k-ωSST模型[11]建立了湍流流体的湍动能k和耗散率ω输运方程：

(1)

式中Pk和Dk为湍动能的生成项及耗散项。

SST模型不能预测层流流动是由于Pk和Dk无法判别边界层流动状态。γ转捩模型的基本思想是建立间歇因子γ输运方程并作用于Pk和Dk(γ=0：层流；γ=1：湍流)，以实现对层流及转捩过程的数值模拟。

(2)

式中：γ输运方程的生成项Pγ=FlengthρSγ[1-γ]；耗散项Eγ=ca2ρΩγFturb(ce2γ-1)。MENTER提出了Reθc与当地湍流度TuL和压力梯度λθ的经验关系式(3)，避免建立Reθc的输运方程：

Reθc(TuL,λθL)=CTu1+CTu2exp[-CTu3TuLFPG(λθL)]

(3)

式中CTu1、CTu2、CTu3为经验系数。

由于SST湍流模型低估了分离点及再附点处湍动能(TKE)生成速率[12]，而γ转捩模型耦合到SST模型后使得层流分离点及分离区内湍动能被进一步限制，导致其预测的层流分离泡过长甚至难以完成转捩再附。为此，本文根据LANGTRY在γ-Reθ模型上提出的分离修正经验关系[7](式4)，将其应用于γ模型：

(4)

γeff=max (γ，γsep)

其中Fθt为混合函数，其值在边界层内为1，主流区为0。

γ模型对SST模型方程中Pk和Dk进行耦合处理,式(5)给出带分离修正γ模型耦合后输运方程(ω输运方程与式(1)相同)，以下简称为SST-γsep模型。

(5)

1.2 算例验证

算例验证模型选用高负荷低压涡轮转子叶栅T106D-EIZ。T106D-EIZ叶栅是在T106A叶型不变的基础上，增加叶栅栅距后获得(由79.9mm增加到105mm)。STADTMüLLER等人[13]在此叶栅上开展了不同雷诺数工况下详细的试验测量。图1为T106D-EIZ叶型示意图。

图1 T106D-EIZ叶型图

为验证SST-γsep模型预测层流开式分离流动的精度，选取文献[13]中的低雷诺数试验工况R6M4作为计算条件，如表1所示。

表1 R6M4低雷诺工况下进出口边界条件

图2、图3分别为有无分离修正模型下T106D-EIZ叶栅表面等熵马赫数曲线、距叶栅出口40mm处损失系数栅向分布与试验结果对比。图2中横坐标表示无量纲的轴向位置(Cx表示叶栅轴向弦长)，图3横坐标表示测点沿栅距方向坐标。式(6)为损失系数ωt的定义式，式中Ptinlet为进口总压，ps为测量位置静压，pb为出口静压。可以看出，相较于原始SST-γ模型而言，带分离修正的SST-γsep模型可以更好地模拟开式分离流动现象，预测的分离泡内压力分布及分离损失与实验结果吻合度更高。

(6)

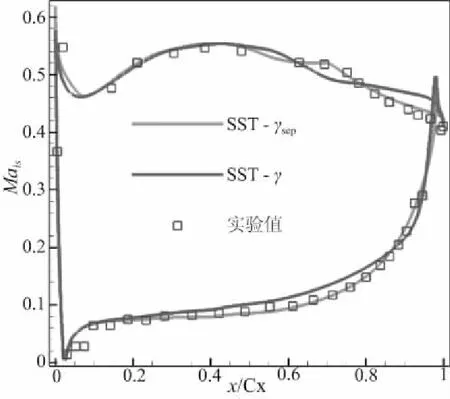
图2 T106D-EIZ叶栅表面等熵马赫数对比曲线

图3 T106D-EIZ叶栅出口40 mm处损失系数ωt

2 结果与讨论

2.1 研究对象及网格

GE-E3五级低压涡轮(low pressure turbine，LPT)是在NASA主持实施高效节能发动机(energy efficient engine，E3)研究背景下的技术成果，具备典型的高性能多级低压涡轮流动特征。GE-E3LPT设计点为最大爬升状态(约11km高空)，物理转速为3511r/min，部件等熵效率试验值为0.915，膨胀比为4.21，折合流量为4.08[14]。

采用单通道定常计算，网格由Autogrid5生成，主流区为HOH型网格，GE-E3LPT转子间隙为0.254mm，网格为HO型，保证第一层网格y+<1，如图4所示。定常计算时转静交界面采用掺混面法，周向边界为周期性条件假设，固壁无滑移，进口总压P*=255kPa，总温T*=1111.9K，湍流度为1%，轴向进气，出口背压pb=55kPa。

图4 GE-E3五级低压涡轮叶型及局部网格示意图

2.2 研究方案及总性能分析

本文主要探讨SST-γsep模型对多级低压涡轮高空流场模拟能力，并给出未加转捩的SST模型计算结果作为对比分析。表2给出有无γsep转捩模型下GE-E3LPT总性能参数，落压比和折合流量基本保持一致；但在设计点，SST-γsep计算得到的等熵效率比SST模型高出约2.9%，与试验效率更为接近(偏高0.3%)。

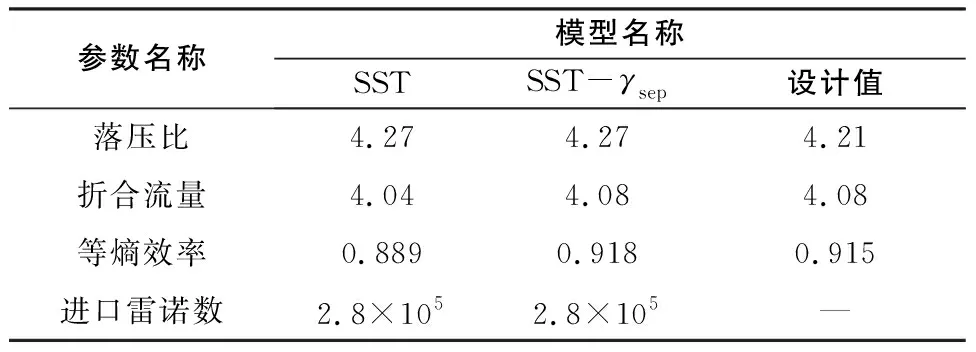
表2 3种模型下GE-E3LPT性能参数表

图5给出了2种计算模型下GE-E3LPT各级落压比、等熵效率分布曲线，各级落压比分布与设计值均较为吻合，表明边界层转捩过程对多级低压涡轮落压比影响相对较小；但SST-γsep模型下的各级等熵效率均高于SST模型(约0.8%～2%)。

图6给出了2种计算模型下GE-E3LPT第1级至第5级等熵效率沿径向分布，横坐标为等熵效率，纵坐标为无量纲径向高度。可以看出，在叶中区域SST-γsep计算结果比SST模型高4%-5%，端区两者相差较小。由于GE-E3LPT不同级效率沿径向分布具有一定相似性，因此仅选择第1级和第5级通道内流场进行分析。

图5 GE-E3LPT各级落压比及等熵效率分布曲线

图6 GE-E3LPT各级等熵效率沿径向分布曲线

2.3 流场分析

图7为GE-E3LPT导叶近壁区湍动能及端区二次流流线图。对于吸力面流动而言，图7(a)中SST-γsep模型预测的边界层大部分为层流状态，在喉道后逆压力梯度影响下出现转捩，湍动能随之增加；在通道涡的作用下诱导端区边界层转捩提前。图7(b)中SST模型全湍流假设使得吸力面近壁区湍动能均处于较高范围。对于压力面流动而言，由于其边界层处于顺压力梯度，且二次流对压力面影响较小，SST-γsep模型下压力面始终保持层流状态(图7(c))，近壁区湍动能明显小于SST模型计算结果(图7(d))。

图7 GE-E3LPT导叶近壁区湍动能及端区三维流线

图8为导叶叶中截面壁面摩擦因数Cf曲线，SST模型预测的壁面剪切应力均显著高于SST-γsep模型结果；SST-γsep在导叶吸力面约75%Cx处Cf迅速增加，对应于边界层转捩过程；而在压力面边界层壁面摩擦因数仅约为SST模型的一半。由此可知，SST-γsep能很好地捕捉边界层转捩过程，预测的叶型摩擦损失更接近实际情况。

图9为第1级转子近壁区湍动能分布及极限流线，可以看出，对于吸力面而言，随着叶片展弦比增加和扩张角减小，端区二次流影响有所减小，叶尖区域泄漏流也会促进吸力面边界层转捩；对于转子的压力面而言，由于前半部分存在逆压力梯度， SST-γsep模型出现小分离泡并诱导边界层转捩，而SST模型未出现分离泡。图10给出第1级转子叶尖间隙内三维流线，流线通过湍动能着色，流体由转子压力面穿过叶尖间隙时湍动能迅速增大，从而诱导吸力面叶尖附近边界层完成转捩。

图8 导叶叶中截面壁面摩擦因数Cf分布曲线

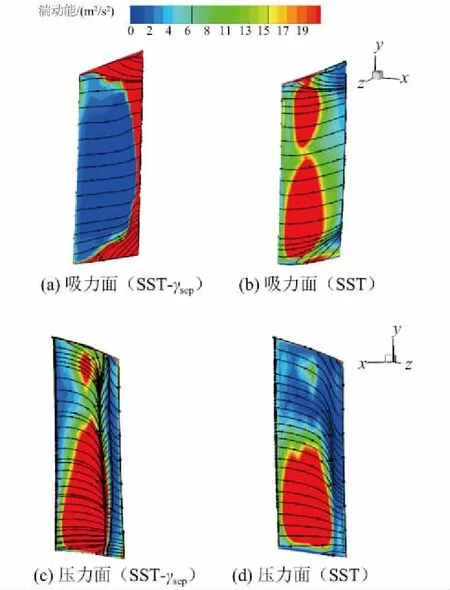
图9 第1级转子近壁区湍动能及极限流线

图10 第1级转子叶尖间隙内三维流线

图11为第5级转子近壁区湍动能云图及表面极限流线，由于最后一级叶片展弦比大，极限流线表现出典型的二维特征。对于吸力面而言，随着雷诺数的降低(相比导叶进口)，在吸力面喉道后逆压力梯度作用下， SST-γsep模型下吸力面边界层出现很小的分离泡，转捩再附后湍动能迅速增加，而SST模型下吸力面未出现分离流动。对于压力面而言，未出现流动分离，但SST模型预测的湍动能仍要高于SST-γsep模型结果。

图11 第5级转子近壁区湍动能及极限流线

总的来说，SST-γsep模型下GE-E3LPT叶片吸力面边界层大部分为层流，喉道后在逆压力梯度作用下转捩为湍流；压力面前段逆压力梯度促使湍动能增加，局部分离并转捩，随着后几级工作雷诺数降低，压力面边界层将为全层流状态。因此，SST-γsep模型叶型损失均要低于SST模型计算结果，使得其预测GE-E3LPT的等熵效率与试验值更为接近。

3 结语

为更准确预测多级低压涡轮中的分离转捩流动，本文在γ模型基础上添加分离修正模型，并在T106D低压涡轮叶栅上验证了此分离修正方法提高转捩分离流动预测精度，将其应用于GE-E3LPT性能及流场数值模拟分析，主要结论如下：

1) 带分离修正的γ模型能够较好地模拟T106D-EIZ叶栅分离泡内压力分布及流动损失，提高对边界层分离的预测精度；

2) 对于GE-E3LPT而言，SST-γsep模型能捕捉到多级低压涡轮中二次流诱导转捩、叶尖泄漏流诱导转捩、分离转捩等流动现象；

3)在高空巡航点工况下，SST-γsep模型预测设计点等熵效率比SST模型更接近试验值，而SST模型假设边界层为全湍流导致叶型摩擦损失急剧增加，低压涡轮整体等熵效率偏低约2.9%。