基于GP-DE算法的土岩二元深基坑参数反分析

文｜辽宁省建筑服务中心 刘铁明；中铁一局集团有限公司 薛永锋

0 引言

在基坑的施工过程中，通过地勘资料得到的地质参数往往具有一定的局限性，不能准确的体现岩土体的地质参数，故往往采用反分析的方法。在以往的运算中，常常将岩土体理想化为单一均质的材料，忽略了复杂的地质条件，导致与实际的结果存在一定的偏差。为了不断满足工程高精度的要求，进行参数的反分析展现了很大的优势。但是土岩二元基坑由于上部为土体，下部为岩层，岩土体参数的确定变得尤为重要，并成为了工程分析中重中之重的关键环节。

近些年，赵志俊运用FLAC3D 计算分析了开挖对基坑周围环境的变形影响机理；张俊峰等通过实测数据对岩层参数反演，并对工程中由于开挖引起的位移变化进行预测；周辉、张传庆等通过研究建立了针对不同类型的屈服准则的屈服接近度求解函数。冯永乾根据实测的支护结构内力和变形，反演出相应的参数。冉涛基于正交试验法设计计算方案，采用FLAC3D进行模拟，并对计算结果进行极差分析和方差分析。施有志基于施工过程的实测数据，提出一套简便易行的考虑土体小应变特性的HSS 模型的刚度参数优化方法。

其中高斯过程算法和差异进化算法就可以应用到具体工程实践中。现将GP、DE算法结合，建立一种求解土岩二元深基坑周围岩体参数的方法。根据正交理论，采用相应的组合方案，通过FLAC3D去计算，采用敏感性分析去得到相应的参数。并使用GP-DE，得到参数与实测项之间的关系，进而对大连地铁5 号线梭鱼湾南站小里程段深基坑地层参数的反演，为施工提供重要的岩土体参数。

1 GP 和DE 算法

1.1 高斯过程算法（GP）

高斯过程(GP)是近几年发展较快的一种机器学习方法。其中任一随机变量t 和对应的状态f(t)的联合概率服从n 维分布。其统计特征由均值和协方差有关：

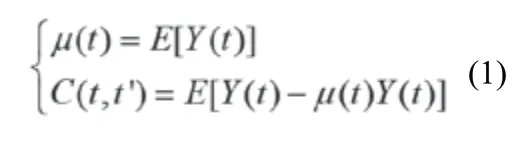
式中：μ (t)为均值，C ( t,t')为协方差，t，t '∈ t均为任意随机变量。高斯过程可定义如下：

1.2 差异进化算法（DE）

Price 和Stom 最先发现了差异进化算法（DE)，并解决了切比雪夫多项式中的拟合问题，其操作为：

（1）种群初始化

首先找到初始点，并随机生成初始种群PG：

式中：G 是进化代数，NP 是种群规模。初始种群 P0中的个体 PG=(xi,1,...xi,j,...xi,n)的第j 个分量为 xi,j。

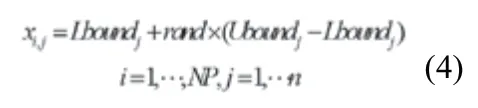
其中，n 表示个体维数，Lboundj和Uboundj分别为分量xi,j的上限及下限，rand表示从[0，1]范围内产生的随机数，并且其服从均匀分布。

（2）变异操作

在进化过程中，DE 利用某种变异策略对种群中的每个目标向量变异。

（3）交叉操作

DE 对变异向量和目标向量进行交叉操作产生试验向量：

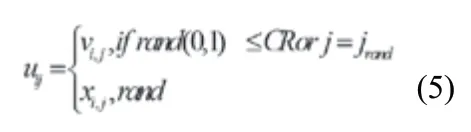
（4）选择操作

选取使得目标函数最小的变量。

1.3 GP-DE 耦合算法

GP-DE 算法可以用到机器学习算法和工程的结合当中，将GP 中的超参数当做初始种群，采用DE 不断寻优，得到最优解。

土岩二元基坑周围岩土体参数反分析的实现步骤为：

（1）参数正交设计：采用正交设计在土层弹性模量、土层内摩擦角、土层粘聚力、岩层弹性模量、岩层内摩擦角、岩层粘聚力的各个取值内形成不同的模拟方案。

（2）样本的产生：通过FLAC3D得到试验样本。作为GP 学习训练样本和预测检验样本。借助敏感性分析选取关键反分析参数。

（3）形成参数与监测变量的关系：采用GP—DE 算法，不断进行样本的GP 过程，直到完成循环过程。

（4）参数寻优：DE 算法适应度函数选用目标函数，并不断寻优找到所需的参数。

2 算法验证

选取如公式6 的函数，验证GP 的性能。式中选取100 组当成训练样本，采用GP-DE 形成对应关系，且预测相应的检验样本。

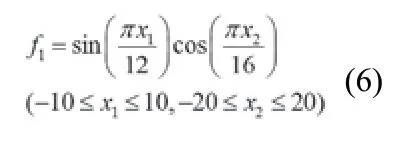
假定DE 中CR=0.7，F=0.8，NP=100，最大进化代数为200，采用协方差函数作为核函数。其结果如下表1所示。

固定CR 为0.7，F 在0.3 ～0.9 中，得到F 越大，越容易变异。F=0.8 收敛比较慢，使得F=0.7 不变，CR 在0.1 ～0.9 中，当CR=0.5 ～0.9，收效好，当CR≤0.3 时，迭代过程变化很大，达到收敛比较困难。因此一定的参数对于算法的收敛性有至关重要的影响（图1）。

图1 不同F、CR 取值搜索迭代收敛曲线

3 工程应用

3.1 工程概况

大连市梭鱼湾南站基坑工程主体结构总长150m，小里程段宽24m，开挖深度为21m，车站为地下3 层侧式车站。围护结构采用全套管钻孔灌注咬合桩+内支撑体系，小里程段桩进入坑底中风化岩约3m。基坑周围地层自上而下依次是：杂填土，厚度为2m；淤泥质粉黏土，厚度为8m；强风化白云岩，厚度为6m；中风化白云岩，厚度为7m。基坑底板位于中风化岩层。

3.2 数值计算模型

取大连地铁梭鱼湾南站深基坑工程小里程段作为研究对象，基坑开挖引起的影响范围一般不超过3 倍开挖深度，因此选择计算模型的三维尺寸为196m×160m×70m。模型共有32928 个节点，28630 个单元。模型如图2所示。

如图3所示，本文选取人工监测点为模型中的7 个点。其中DBC1-5、DBC2-5、DBC3-5 三点为基坑周围Z 方向的沉降监测点，选取桩1-4 分别监测其桩顶、桩身4 米处、桩身12 米处和桩身16 米处的倾斜程度。

3.3 正交计算及敏感性分析

基坑主要分布上软下硬的土岩二元地层中，由于首层土为素填土且相对地层较薄，因此选取第二层淤泥质粉黏土以及第三层强风化白云岩的弹性模量E、粘聚力c和内摩擦角φ 来进行敏感性分析及反分析。E1为淤泥质粉黏土的弹性模型，c1、φ1为其粘聚力和内摩擦角，E2为强风化白云岩的弹性模型，c2、φ2为其粘聚力和内摩擦角。下表2为正交计算参数取值范围。

图2 三维计算模型图

图3 监测点布置图

根据正交方案，采取L25(55)正交表，依照地勘资料，采取不同的组合方式，选取地表点DBC1-5、DBC2-5、DBC3-5 和桩体位移监测点CX1-4（4 米处）、CX1-4（8米处）、CX1-4（12 米处）、CX1-4（16 米处）7 个监测点。表3和表4分别为正交计算表和测点位移值。表5为不同参数对测点的影响次序。

表1 函数f1 预测对比

表2 参数取值范围

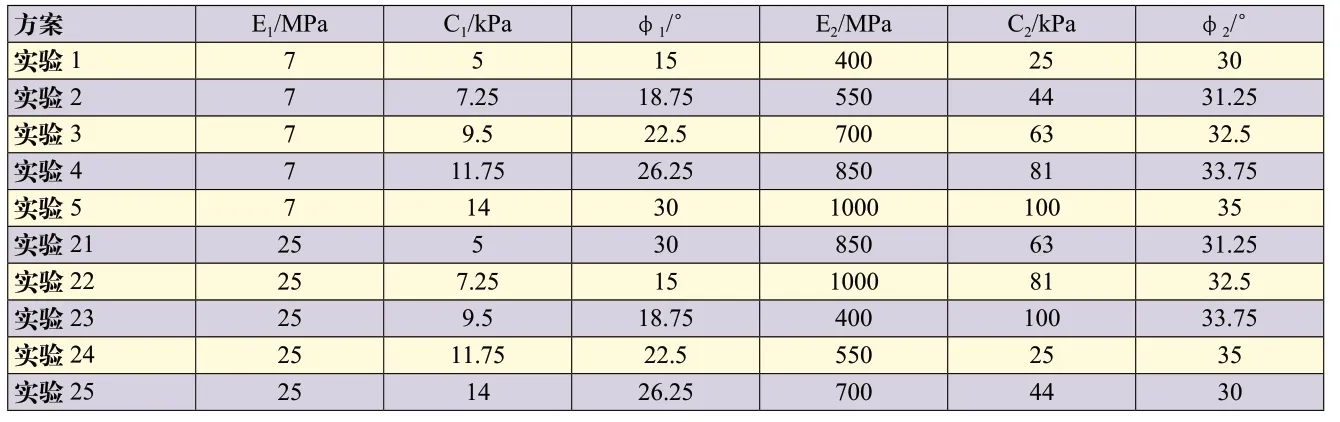
表3 正交计算表

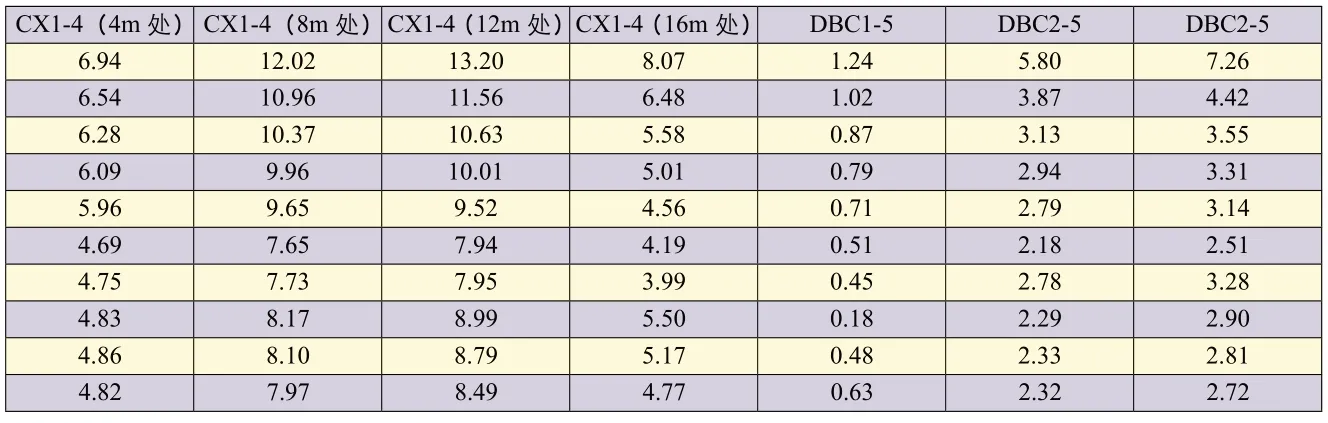
表4 测点位移值

表5 极差计算值及次序值

表6 反分析结果表

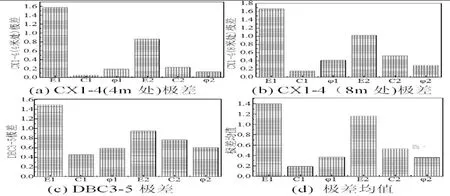
图4 各测点极差柱状图

表7 反演计算结果与实测结果

由图4（d）极差均值柱状图看出，正交试验设计的六个因素中对监测点位移影响的敏感度依次为：E1，E2，C1，C2，φ1，φ2。参数E1的极差均值为1.400，E2极差均值为1.158，这两个参数影响值远大于其他因素，这意味着参数E2、E1对位移的影响最为明显。参数C2，φ2，C1，φ1的取值对基坑周围土层变形影响相差不大，因此得出结论，基坑开挖过程中土体的弹性模量的取值对基坑位移的影响程度要大于土体内摩擦角和内聚力的取值。

选择实测值当做控制值进行反演，其中DE 中的CR=0.7，F=0.8，最大进化代数=200，NP=100。其中选取基坑表面相对应断面的五个监测点CX1-1（桩顶）、CX1-1（4m 处）以及地表沉降监测点DBC1-3、DBC2-3 和DBC3-3 监测值，将与之运用反分析计算结果对比。反分析结果见表6。

利用上述反分析地层参数进行数值计算，将计算结果与现场实际监测数据进行对比，见表7，由表可见，两者比较接近，其相对误差最大值24.03%，其数值相差1.87mm 相差很小，验证了反分析结果的准确性。

4.结论

（1）本文将设计正交、GP 算法、DE算法相结合，建立一种基坑周围岩土体参数的反分析方法。利用敏感性分析分析影响最大的参数，并采用GP-DE 算法求解具体的参数。

（2）对实际工程的参数采取反分析，随后进行正算，和其实测数据对比可得，其误差很小，表明此算法能够满足精度要求，效果较好。