巧用圆的几何性质求解解析几何题

刘建华

(江苏省扬州大学附属中学,225000)

解析几何作为高中数学的重要内容之一,一直在高考试题中占据重要地位.这类题往往综合性强,求解过程复杂繁琐,使不少学生望而生畏.其实，在解题过程中,如果巧妙运用数形结合,比如平面几何中圆的几何性质,不仅可以避免由于方法繁琐以致得不到正确答案的困惑,而且能在轻松解决问题的过程中充分感受到数学的魅力.

一、利用圆的定义

平面内到定点距离等于定长的点的轨迹是以定点为圆心,定长为半径的圆.在求动点轨迹方程时,如果能依据题目条件及图形特点,分析出定点和定长,则由圆的定义可以直接确定点的轨迹.

解如图1,分别延长F1P和F2A交于点B.易知∆ABF1是等腰三角形,AB=AF1，且P是F1B的中点.

由圆的定义，可得点P的轨迹是以O为圆心,4为半径的圆.所以，点P的轨迹方程为x2+y2=16.

评注此题抓住关键条件AP既是角平分线,又是垂线,根据等腰三角形的三线合一,得到P为线段BF1的中点;再由椭圆的对称性知O也是F1F2的中点,由中位线性质得OP为定长,从而确定点的轨迹,避免了用解析法求方程的繁琐运算.

二、利用圆周角性质

在同圆或等圆中，同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等;一条弧所对的圆周角等于它所对的圆心角的一半.解析几何题经常涉及角的大小问题,此时不妨利用圆周角的几何性质构造出圆，并巧用其性质解题.

若切点Q在x轴上方(如图3),因为直线l在x轴上方的所有的点(除点Q)都在圆外,由圆的几何性质可知,这些点对点F1、F2的张角均小于∠F1QF2；若切点Q在x轴下方,同理可知∠F1QF2即为所求的最大角.

由圆M经过F1、F2两点,可知圆心M在y轴上.又因为圆M与右准线l相切,故圆M的半径r=OP=2.连结MF1、MF2,有

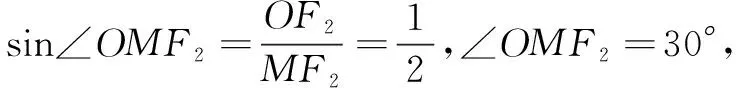
评注此题由题中条件∠F1QF2为动点P对两定点F1、F2所张的角,联想到圆周角的性质构造圆,并结合题中条件,找出角之间的大小关系,确定最大角,从而使得问题简单直观,目标明确.

解先确定临界状态,即∠F1PF2为直角时点P的横坐标.若∠F1PF2为直角时,则点P在以F1F2为直径的圆x2+y2=6上(如图4).

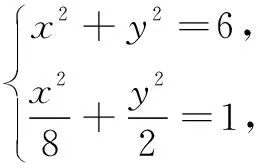
三、利用垂径定理及推论

对于一个圆和一条直线来说，如果这条直线具备下列五个条件中的任何两个，那么它也一定具有其它三个性质:① 垂直于弦;② 过圆心;③ 平分弦;④ 平分弦所对的优弧;⑤ 平分弦所对的劣弧(当以③ 为题设时，“弦”不能是直径).

例3已知平面上点P(2,2),圆C:x2+y2-8y=0.过点P的动直线l交圆C于A、B两点,M为线段AB中点.

(1)求点M的轨迹方程;

(2)当OP=OM时,求直线l的方程及∆POM的面积.

解(1)圆C的方程可化为x2+(y-4)2=16,故圆心C(0,4),半径为4.

(2) 由OM=OP，知点O在MP的垂直平分线上(如图5).

评注此题根据弦的中点、弦的垂直平分线等条件多次使用了垂径定理及其推论,通过寻求图形的几何关系,不断将问题转化,使得解法简洁清晰,提高了解题效率.

四、利用直线与圆、圆与圆的位置关系的判定

直线与圆的位置关系分为相交、相切、相离.判断具体的位置关系有两种方法:一是确定直线与圆公共点的个数;二是用圆心到直线的距离d与半径r的大小关系判定直线与圆的位置关系.反之,也可由直线与圆的位置关系得到d与r的数量关系.

圆与圆的位置关系分为外离、外切、相交、内切、内含.判断具体的位置关系也有两种方法:一是确定圆与圆公共点的个数;二是用圆心距d与两圆半径之和r1+r2、半径之差|r1-r2|的大小关系判定圆与圆的位置关系.反之,也可由两圆的位置关系得到圆心距d与两圆半径之和r1+r2、半径之差|r1-r2|之间的数量关系.

解圆M：(x-6)2+(y-7)2=25,故圆心M(6,7)，半径r=5.

由Q(x2,y2)在圆M上,得(2+x1-t-6)2+(4+y1-7)2=25,即(x1-t-4)2+(y1-3)2=25,故点P在以N(t+4,3)为圆心,5为半径的圆上.

评注在此题中,先设出点的坐标,代入题目中的约束条件,得到点坐标满足的方程;再根据方程的结构特征确定动点在两个圆上运动,将点的存在性问题或方程组有解问题化归为两圆的位置关系的判定,使问题迎刃而解.

五、利用切线性质

经过半径的外端且垂直于这条半径的直线是圆的切线;圆的切线垂直于过切点的半径.在圆的切线问题中,可以利用切线的几何性质得到直线间的垂直关系,从而进一步解题.

①

评注此题经过伸缩变换,将椭圆转化为圆,求椭圆的切线问题转化为求圆的切线问题.由于圆中几何性质更为明显,故可直接应用几何性质解题,易于理解,也避免了大量的运算,只需最后还原即可.

变式已知P是直线l:3x+4y+8=0上的动点,PA、PB是圆x2+y2-2x-2y+1=0的切线,A、B是切点,C是圆心,那么四边形PACB面积的最小值是______.

解如图7,由题意,圆的方程可化为(x-1)2+(y-1)2=1,故圆心C(1,1),半径为1.

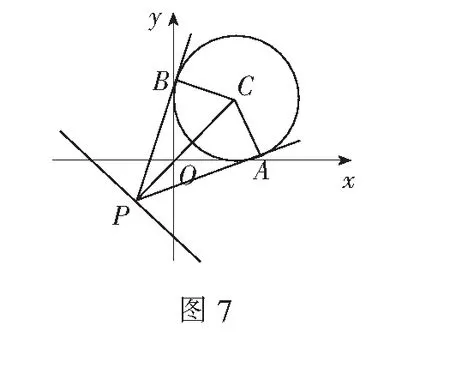
由此可见，当PC最小时,四边形PACB的面积最小.

数形结合思想是数学解题中重要的思想方法，它可以使某些抽象的数学问题直观化、生动化,呈现出问题的本质规律和数学的内在美.在解决解析几何问题的过程中,需要我们有一双善于发现的眼睛,找出题中隐含的与圆相关的几何条件或代数关系；通过构造或转化,结合圆的几何性质,简化运算过程;解题方法也从“单一”走向“灵活”.这将有助于培养学生敏锐的观察力、创造性的想象力等思维品质.