工程振动测试技术中实验模态分析方法的改进

李雪艳，许俊财

（暨南大学力学与建筑工程学院 “重大工程灾害与控制”教育部重点实验室，广州 510632）

0 引言

《工程振动测试技术》是中国高校力学、土木、机械类专业选修课，旨在培养相关专业学生的振动测试和振动信号分析能力[1]。工程振动测试技术是一门综合性技术，集振动理论、动态测试技术、信号分析和系统参数识别等多学科于一体，通过理论分析与试验研究相结合以达到工程测试的目的。目前工程振动测试技术的地位越来越重要，是人们认识客观事物的重要手段，主要包括测量技术与试验技术。在动态测试过程中，需要借助专门设备，通过试验和数据处理，得到所研究结构的有关振动信号[2-5]。

实验模态分析是 《工程振动测试技术》的一个重要内容，它是研究复杂机械和工程结构振动的重要手段。模态参数是结构的固有振动特性，每一个模态都具有特定的固有频率、阻尼比和模态振型。这些模态参数可以由计算或实验分析得到，这个计算或实验分析的过程称为模态分析。

如果通过实验设备将采集的系统输入与输出信号经过参数识别获得模态参数，就称为实验模态分析。实验模态分析通常是对结构进行动力学激振，由响应的信号求得系统的频响函数矩阵，再采用多种识别方法，最终得到结构固有的模态参数。传统的实验模态分析方法可以分为频响函数法（测力法）和环境激励法（不测力法）两种：①频响函数法为在实验过程中测量激振力和响应的方法，实验模态分析是通过对激振力和响应的时程进行频率分析，求得系统的频响函数 (或传递函数)，然后采用参数识别法求出结构的振动模态和结构参数；②环境激励法为在实验过程中不需要测量激振力的方法，因为实际工程中的大量结构和机器（如大型建筑、桥梁、大坝等）都是很难人工施加激振力的，结构的响应主要由环境激励引起，其激振力也很难测出，如车辆行驶时的振动以及地脉动等各种环境激励，而这些环境激励既不可控制又难以测量[6-8]。

频响函数法在得到频响函数以后，可以继续得到幅频曲线、实频曲线和虚频曲线等，然后由峰值法确定结构的频率，再进一步计算确定结构的阻尼和振型。峰值法（Peak picking method）是最简单的频域结构模态参数识别方法，它假定所测结构的动力响应只由一种模态确定，因此较适合模态可以很好地分离且阻尼较小的情形，具有处理简单、快速、实用等特点[9-10]。但是峰值法需要进行傅里叶变换，在一定的窗口宽度上进行平均处理，这样的处理会忽略一些细节，因此峰值法不可避免的存在本质上的不足：由于该方法要求结构模态频率均匀分布，对于高耸结构如烟囱、水塔等，结构空间扭转模态和弯曲模态的特征频率会有比较接近的值，使用峰值法会出现遗漏或误差；另外，峰值的选取也具有主观性。尽管存在以上不足，但是峰值法识别模态参数速度快，容易操作，所以在现有工程振动测试的教材中主要还是使用该方法。

而近年来，随机子空间法被广泛应用于实验模态参数的识别。随机子空间方法（Stochastic Subspace Identification method）是1995年以来国内外模态分析方面专家和学者讨论的一个热点[11-14]。该方法基于离散时间状态空间方程，是直接处理时间序列的时域方法，输入由随机白噪声代替，适用于环境激励条件下结构模态参数的识别。随机子空间方法适合土木结构尤其是桥梁等实际工程的系统识别问题，能够比较准确的识别结构模态参数。其理论严密、算法清楚，便于计算机软件实现。本文拟把随机子空间法拓展到适用于所有激励情况下的实验模态分析，即可以适用于包括冲击激励、简谐激励和环境激励等多种情况下的模态参数识别，以便可以被学生掌握该方法和将该方法应用到实际的工程结构振动分析中。

1 随机子空间法

基于协方差的随机子空间法主要从输出数据构建的Hankel矩阵，去构造其数据协方差的Toeplitz矩阵，然后进行奇异值分解，由此得到矩阵行和列空间中拓展的可观测矩阵和逆向扩展的可控制矩阵。利用拓展的可观测矩阵的推移不变特殊性质得到系统的状态矩阵，进而得到结构的模态参数。

1.1 构建Hankel矩阵

如分析的系统为线性时不变系统，输出响应为y（t）。设定i为时刻点，j为离散的时间序列，通过输出数据构建如下的Hankel矩阵[15]：

将Hankel矩阵划分为上下两个部分，有两种分类形式，一部分代表过去输出（past），一部分表示未来输出（future），可以表示如下：

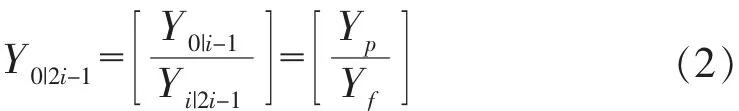
1.2 输出协方差矩阵

结合实际输出的同一时间内j组输出向量，假设输出有各态历经性，则系统的输出协方差矩阵可以表示为以下形式：

1.3 由协方差构建的Toeplitz矩阵

输出协方差构建的Toeplitz矩阵表示如下：

可进一步表示为：

其中A为离散状态矩阵，由其特征值即可求得系统的动力特征值，C为离散输出矩阵，G为状态输出协方差矩阵，Oi=[C CA…CAi-1]T成为拓展的可观测矩阵；为逆向拓展的可控制矩阵。

1.4 Toeplitz矩阵分解

对Toeplitz矩阵进行奇异值分解可得如下表达：

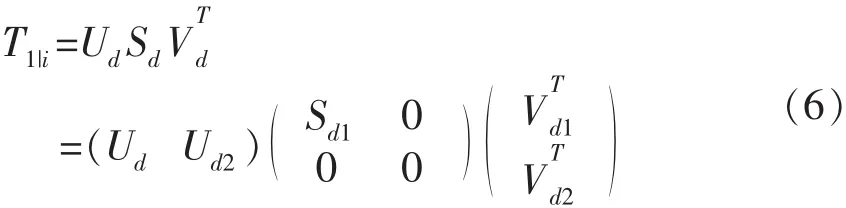
其中Ud、Ud为正交矩阵，Sd为奇异值所组成的对角矩阵。进而可以得到以下关系，

1.5 状态矩阵A的求解

拓展的可观测矩阵包含了状态矩阵A，取Oi的i-1行， 得到和，表达如下：

所以两者的关系为：

因此状态矩阵A可由下式求得，

其中（·）+为广义逆的表达。由于需要进行广义逆计算，当输入信号中含有噪声时，容易引起该重构状态矩阵扰动，导致最后出现大量虚假模态。本文通过忽略高阶分量以得到更稳定的状态矩阵，从而有效提高了稳态图的质量和最后的模态参数识别精度。

1.6 连续状态矩阵Ac和离散状态矩阵A的关系

对离散状态矩阵A进行特征值分解可得：

其中Λ=diag[ui]，ui表示离散复特征值，即Λ表示各阶复特征值组成的对角阵，Ψ表示特征向量组成的矩阵。

同理，连续状态矩阵进行特征值分解之后的表达式为，

其中 Λc=diag[λi]， λi表示连续复特征值。

由于A=eAcΔt，所以有：

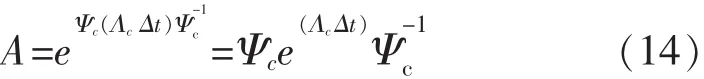
由此可知，连续状态矩阵和离散状态矩阵分解出来的特征向量是一致的，它们之间特征值的关系如下:

1.7 系统的复特征值与固有频率、阻尼比之间的关系

系统的复特征值与固有频率、阻尼比之间的关系有如下式子:

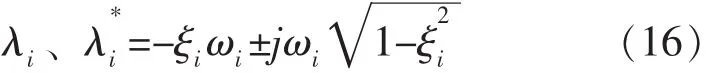
其固有频率ωi、阻尼比ξi和振型Φ为:

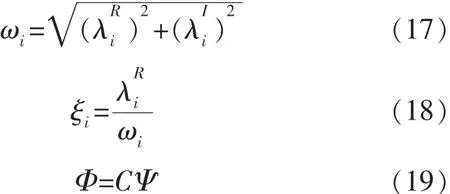
2 七层框架模型实验模态分析

图1（a）所示的七层钢框架结构进行数值模拟分析，来演示基于随机子空间法的实验模态参数识别。每层竖向柱子被分成两个等长的梁单元，每层横向梁被分成三个等长的梁单元，结构有限元模型的单元和节点编号系统如图1（b）所示， 总共56个平面梁单元，51个节点，每个节点3个自由度，共153个自由度。结构每层柱子高为0.3米，共2.1 m，柱横截面为长50 mm、宽8.92 mm的矩形，横向梁长为0.5 m，截面为长50 mm、宽4.85 mm的矩形，材料弹性模量为E=200 GPa，结构中柱的质量密度和梁的质量密度分别为7850 kg/m3和 7734 kg/m3。

为了模拟楼板的质量，每层分别加了两对质量块，每一对质量块重量为3.9 kg。框架的底部被固支，横向、竖向和转动方向的约束由大刚度1.0×1010kN/m， 1.0×1010kN/m 和 1.0×109kNm/rad来代替。采用瑞利阻尼，前两阶阻尼比为ξ1=ξ2=0.01，其它阶阻尼比由ΦTCΦ/（2ω）计算得到，Φ为振型矩阵，C为阻尼矩阵，ω为模态频率向量。通过特征值分析，得到结构的前三十阶频率为1.7616， 7.1044，12.3851，14.5004， 17.7541， 22.0517， 249.3672， 253.2250， 257.7560， 259.181 1， 261.7788， 266.3669， 267.9939和 273.7268 Hz，如表1所示。取时间步长为0.001 s，在第2节点处作用水平方向的三角脉冲激励，激励峰值为320.4 N，持续0.005 s。采用逐步积分法，计算该七层框架结构各节点的加速度响应来模拟测试得到的加速度响应。假定在第3到第8节点 “安装”加速度计记录测试这些节点6 s内的水平向加速度响应；计算这些节点的频响函数，得到幅频曲线如图2所示。

图1 七层框架结构 （单位：m）Fig.1 The seven-floor frame structure （unit： m）

通过该曲线，由峰值法可得到的频率为：1.465， 7.324， 12.21， 14.65， 17.58， 21.97， 25.8 8，28.32 Hz（如表1所示），而其它的峰值则不明显，所以更高阶的频率通过峰值法无法识别得到。

图2 来自六个测点的幅频曲线Fig.2 The amplitude frequency curves of acceleration responses from six measurement locations

如果把这六个测点的加速度响应，使用随机子空间法进行分析，那么可以得到如图3所示的稳态图，图3（a）为整个频率范围的稳态图，图3（b） 、（c） 、（d） 分别为 0～60 Hz、 60～120 Hz、 120～240 Hz之间的稳态图。识别出来的频率分别为1.762， 7.103， 12.38，14.49，17.74， 22.02， 25.8 6， 28.43， 40.11， 41.84， 43.61， 45.47， 47.55， 4 8.66， 71.34，102.3， 103.3，105.2， 106.9， 108.9， 109.4， 158.5， 219.2， 224.4 和 230.0 Hz， 如表1所示。

通过跟结构质量矩阵和刚度特征分析得到的频率进行比较，从表1可以看到，峰值法仅能识别前八阶频率，而随机子空间法则可以识别前二十五阶频率，且前十五阶频率最大误差低于1.7%，而峰值法的误差则最大达到3%。可见，无论从识别的频率阶数还是从精度上，随机子空间法都更有优势。

表1 通过三种途径得到的频率Table 1 The identified frequencies using three methods

3 简支钢梁实验模态分析

对如图4所示的简支钢梁进行实验室测试，来进一步演示本文提出的实验模态分析方法。采用的钢梁长1996 mm，截面为宽50.75 mm、深9.69 mm的矩形，杨氏模量为191.1 GPa，密度为7790.6 kg/m3。钢梁两端简支，支座间跨度为1920 mm，如图4所示七个加速度传感器被等间距安装在钢梁上表面，采样频率2000 Hz。在距梁右端638 mm处的上表面，用锤子进行敲击产生振动，使用商用数据采集系统INV303和数据分析系统DASP2003测试并记录加速度，进行多次重复测试。通过频响函数和局部峰值拾取法，可以得到结构的前十阶频率如表2所示。通过随机子空间法得到的0～300 Hz之间的稳态图如图5所示，从表2可见，随机子空间法能识别得到结构的前十二阶频率。因此，在本模型实验中，随机子空间法也能识别到更多的频率阶数。

图3 来自六个测点的稳态图Fig.3 The stabilization diagrams of acceleration responses from six measurement locations

表2 基于频响函数+峰值拾取法和随机子空间法识别出的频率Table 2 The identified frequencies using the peak picking method of frequency response function and the stochastic subspace method

4 结语

鉴于工程振动测试技术教材中基于频响函数的实验模态分析技术具有识别模态阶数较少等局限性，本文应用随机子空间法来对一般激励下的振动响应进行模态参数识别。基本原理是对测试得到的振动响应，构建Hankel矩阵和Toeplitz矩阵，然后进行奇异值分解，并构建结构的状态矩阵进行模态参数识别，形成稳态图，最后识别出结构频率。通过数值算例和模型实验，发现该方法能识别得到更多阶数的频率，并且具有更高的精度。

该方法可作为现有工程振动测试技术中实验模态分析法中频响函数峰值法教学的有益补充，提高学生的能力和兴趣。该方法也便于计算机编程计算，适合在实际工程结构的模态分析中应用。

图4 实验室测试的简支钢梁Fig.4 Schematic diagram of a simply supported steel beam tested in the laboratory

图5 实验室测试简支梁在0～300 Hz之间的稳态图Fig.5 The stabilization diagram of acceleration responses of the simply supported beam with 0-300 Hz