高层建筑桁架转换层地震反应线性分析方法研究

潘冰

（新疆铁道勘察设计院有限公司，乌鲁木齐 830000）

0 引言

随着科学技术的进步和社会经济的发展，高层建筑的数量和高度逐渐增加，且建筑结构的体型和功能均朝向多样的综合性方向发展。高层建筑结构对空间的需求越来越高，通常均需要采用转换层结构，现存的建筑转换形式中转换桁架具有受力精准、结构自重和抗侧刚度小的优势[1]，有助于室内通风采光和大型管道的安装布置，在高层建筑应用中具有较好的功能结果和艺术设计效果，因此桁架转换在高层建筑中应用较广，在地震作用下带有桁架转换层的高层建筑稳定性受到破坏，因此研究高层建筑桁架转换层在地震作用时的地震反应十分必要。

本文以非线性空间有限元结构计算软件为理论计算手段，对高层桁架转换层的地震反应进行模态分析，研究高层建筑桁架转换层结构的地震反应变化。

1 桁架转换层地震反应非线性分析方法

1.1 桁架转换层结构有限元建模

非线性分析桁架转换层地震反应时，对高层建筑桁架转换层的地震反应分析选择SAP2000程序中的平面壳单元和杆系单元进行建模分析[2-4]，建筑材料参数确定根据材料性能试验的试验获取值和规范值确定，将钢筋混凝土材料视为均匀分布材料，该材料特性用单一本构关系表示，采用叠加原理对钢筋混凝土的容重和弹性模量等特性实施等效处理，且将钢筋混凝土的容重规定为25.6 kN/m3。

1.2 模态分析

模态分析也为振型叠加法动力分析，为线性结构地震反应分析的常用方法，该方法可在完成一组正交向量分解后，将大型方程简化为数量相对降低的解耦二阶微分方程[5]，降低数值计算方程用时。

采用SAP2000程序对高层建筑桁架转换层进行有限元建模，模型将提供建筑基本性能参数，对建筑地震反应进行模态线性分析，包括高层建筑桁架转换层的静力地震作用分析和静力风载荷作用分析[6]。

（1）将高层建筑桁架转换层动力反应方程转换为微分方程地震作用下高层建筑桁架转换层结构的体系动力平衡方程如公式 （1）所示：

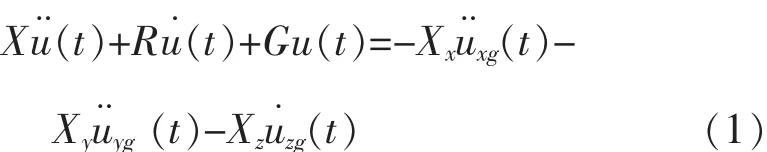
其中，R表示阻尼矩阵，为建筑节点相对地面的运动加速度。X表示质量，G为刚度，Xx、Xy和Xz为桁架转换结构的单向有效质量，和u为地面运动的单向加速度。

将该式转换为Nd二阶微分方程：

其中，fj和J表示空间向量与时间无关，gj（t）表示第j个与时间相关函数，通常高层建筑桁架转换层地震反应分析需考虑的动力载荷包括风载荷和地震作用均采用上述空间向量乘积表示。

动力自由度个数为建筑中集中节点质量的个数，通过对式（2）实施静力凝聚以降低桁架转换层的无质量位移且减少需计算动力平衡方程个数[7-9]，高层建筑桁架转换层模型结构分析时，视某楼板为水平刚性且刚性楼板仅表现为包括三个方向自由度的集中质量。

（2）生成模态方程。计算式（2）采用分离变量法，若要完成变量分离，可将式（2）的解表示成公式（3）：

公式（3）中λ为Nd×N矩阵，其中包括N个非时间函数的空间向量，Y（t）包括N个时间函数的空间向量，因此将公式 （3）表示为：

计算公式（4）前，公式（4）中空间函数需满足：λTXλ=I和 λTGλ=δ2条件，且I为对角矩阵，δ2表示对角矩阵中对角项为的矩阵。

将公式（3）和（4）代入公式（2），获取公式（5）包括N个未知数方程：

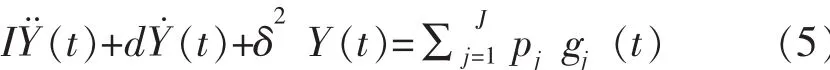
式（5）中，pj=λTf， 其含义为：pj表示载荷函数j的模态参与系数，且d表示阻尼矩阵，为解耦公式 （5）， 将模态阻尼的对角项设为dm=2ξnωn， 振型间不存在耦合的典型阻尼。ξn表示第n振型中阻尼与此时对应振型的临界阻尼比，则公式（5）为：

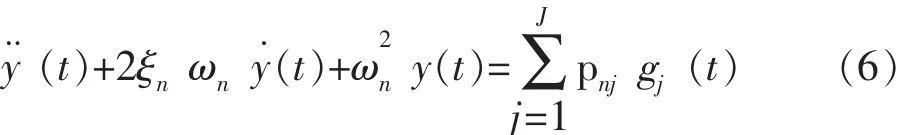
公式（6）为非耦合典型线性高层建筑桁架转换层结构的模态方程，地震运动模态方程表示为：

建筑结构振型和外部激励共同决定振型参与系数，振型参与系数是加速度荷载与振型的积[10-12]，对于整体桁架转换层在X、Y和Z三方向加速度的载荷的振型n的参与系数为:

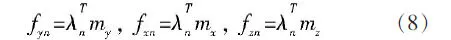
其中，mx、my和mz分别为转换层在X、Y和Z方向的单位加速度荷载，且获取的fxn、fyn和fzn参与系数指示每一振型分别由加速度载荷激励的强度。

振型基于公式（9）质量矩阵进行正规化：

式（9）质量表示振型质量，同时将振型刚度定义为：

由高层建筑建设规定可知，高层建筑结构常采用振型分解谱法进行地震分析，通过分析模型多个振型可知前几阶振型参与系数较大，且参与系数与阶数呈相反趋势，表明在计算桁架转换层地震效应时，主要其控制的为前几阶振型。

1.3 地震反应谱分析

地震反应谱分析是将建筑结构模态分析的振型刚度与地震反应谱联合获取桁架转换层抗震设计反应谱，以抗震设计反应谱为依据进行地震动力分析。反应谱法通过动力方法计算高层建筑桁架转换层地震反应[13]，综合考虑地震造成的地面运动强弱、地面土地性质和结构特性对地震惯性影响，可较好的反应地震对高层建筑桁架转换层的影响。

反应谱为单质点体系在一定地震加速度作用时的地震反应随自振周期的变化曲线，也是阻尼的函数[14]。不同地震加速度、土地性质以及建筑结构自振周期和阻尼等对地震反应曲线影响均不相同，且反应谱曲线是根据单质点体系 （桁架转换层）的动力计算得到[15]，在地震加速度作用下，依照反应谱理论得到的最大地震作用F：

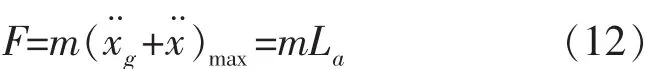
此时作用在桁架转换层的最大剪力V表示为：

其中，La和Ld分别表示加速度反应谱和位移反应谱，桁架转换层的刚度和质量分别为G和m。因为加速度反应谱和位移反应谱间存在如下关系：

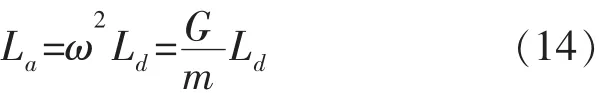
将式（14）代入公式（13）可得：

从式（15）可知，桁架转换层根据反应谱法计算得到的地震作用F与底部最大剪力V一致。上述关系针对多质点体系仅可获取近似结果，高层建筑桁架转换层结构的地震水平力可转换为等效侧向力，当完成等效侧向力计算后，高层建筑桁架转换结构地震反应可采用静力学方法解决。

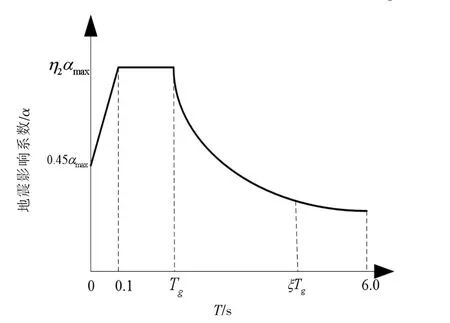
图1 地震影响系数曲线Fig.1 Seismic effect coefficient curve

图1中直线上升阶段、水平段、曲线快速下降和曲线缓慢下降阶段分别存在如下关系式：

上述各式中，α和αmax分别表示地震影响系数及其最大值，η1和η2分别表示下降段斜率调整系数和阻尼调整系数，k为衰减系数，T为桁架转换层自振周期。

且k、 η1和 η2取值分别为：和

针对地震作用时高层建筑桁架转换层的多条加速度记录，选取阻尼比ξ为0.005，获取该阻尼比时的加速度反应谱，并除以各条加速度记录最大值，统计分析获取综合平均结果并进行平滑操作获取标准反应谱，然后将该结果与地震系数相乘，得到高层建筑桁架转换层的抗震设计反应谱，根据获取的反应谱动力计算高层建筑桁架转换层的地震反应。

2 实例分析

2.1 SAP2000分析模型

实验采用本文方法对高层建筑桁架转换层地震反应非线性分析时，研究对象建筑结构为带钢桁架转换层的15层框架结构，有限元模型如图2所示，梁截面尺寸和柱截面大小均为450×750 mm和750×750 mm，转换层下柱截面和框支柱大小分别为850×850 mm和1050×1050 mm，转换层桁架的上下弦杆为箱截面，尺寸大小为650×650×45 mm， 斜腹杆为尺寸大小为650×650×35×35 mm的H型钢，建筑各钢筋构件、混凝土构件和钢构件间连接方式均为铰接，钢构件与钢筋混凝土间连接通过预埋钢板构件实现。

2.2 模态分析结果

通过对图2分析模型进行模态计算，得到高层建筑桁架结构共30个自振周期，模型结构在不同振型时的自振周期曲线如图3所示。

从图3曲线可知，高层建筑桁架转换层模型结构的自振周期在前3阶振型时较大，5至8阶振型自振周期虽较大，但明显低于前3阶，此后9至30阶振型的自振周期非常小，因此分析高层建筑桁架转换层地震作用反应时，主要起作用的振型为前8阶振型。

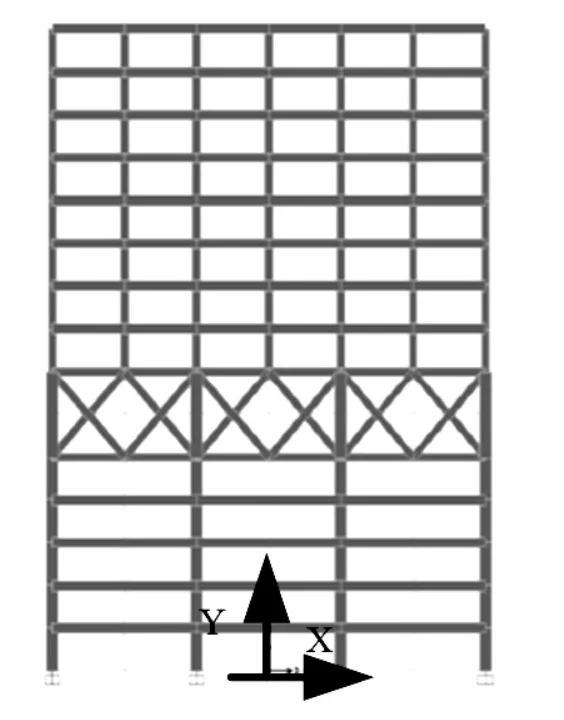
图2 SAP2000分析模型Fig.2 SAP2000 analysis model

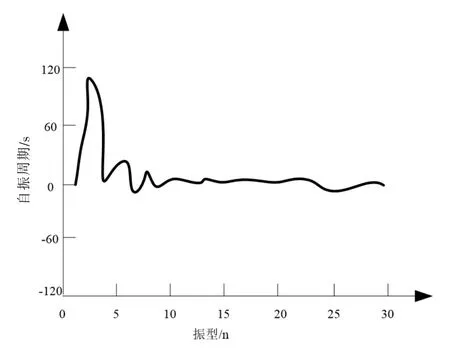
图3 自振周期图Fig.3 Natural vibration period diagram

2.3 位移和剪力分析

当高层建筑桁架转换层受X向水平地震作用时，建筑结构整体变形中X向位移较大，反之受Y向水平地震作用时，建筑结构整体变形Y向位移较大。在处理位移数据时，先得到建筑各层的位移或位移角变化，然后根据位移或位移角变化反映建筑各楼层变形的规律，图4和图5分别为建筑结构受到X方向地震和Y方向地震时的楼层位移曲线和层间位移角曲线。

从图4和图5可知采用本文方法计算得到高层建筑顶层在受到X向和Y向地震后的最大侧位移分别为12.21 mm和16.12 mm，建筑结构的层间位移角均小于1/800。且图4中的层间位移曲线在6楼时发生突变，是由于建筑层高的不同，导致5楼的刚度小于6楼，因此层间位移在6楼时发生突变。

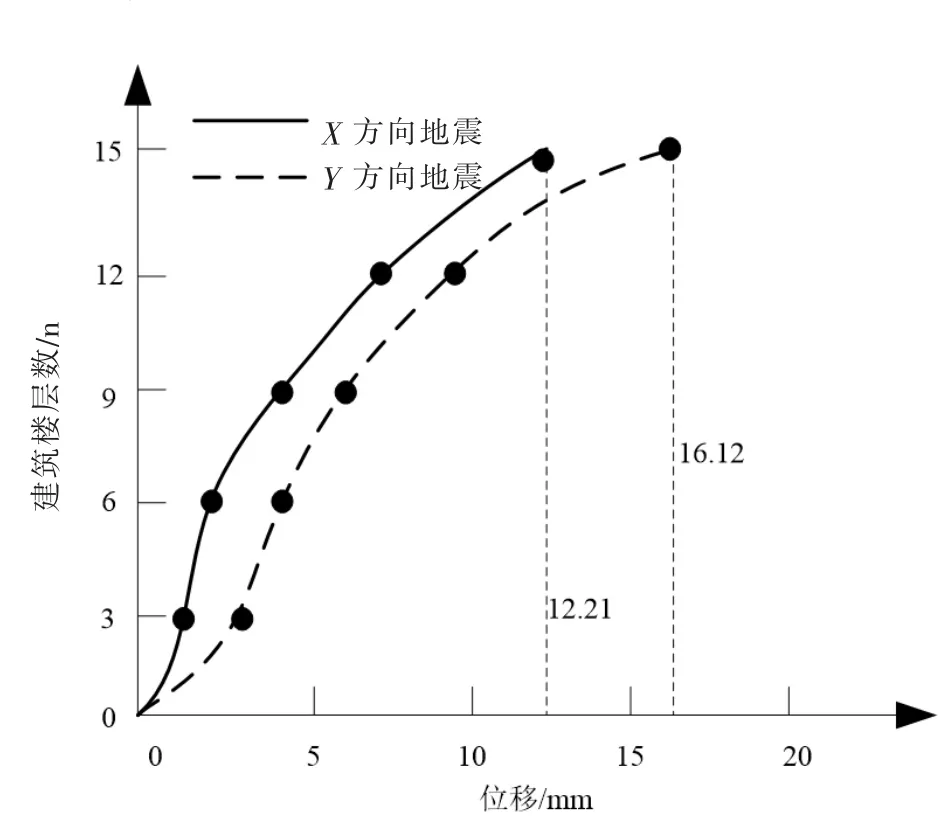
图4 建筑结构楼层位移曲线Fig.4 Floor displacement curve of building structure

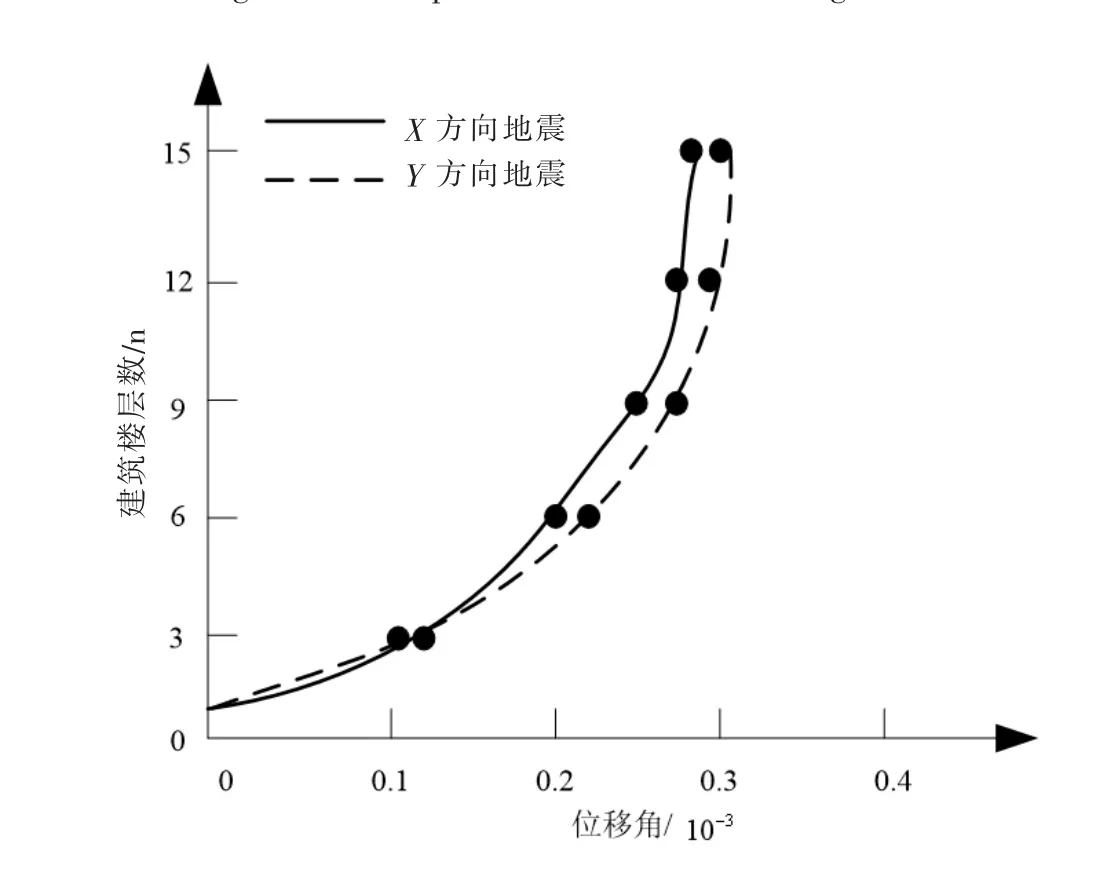
图5 建筑结构楼层间位移角曲线Fig.5 Displacement angle curve between floors of building structure

地震作用下由于高层建筑设置桁架转换层，导致建筑转换层所在楼层刚度增长幅度较高，因此桁架转换层及其邻近楼层的位移较小，图5层间位移角在转换层较其上、下层略小一些，即转换层上、下层间容易出现层间位移角突变现象，说明高层建筑桁架转换层能使建筑结构发生竖向刚度突变。且经本文方法计算得出，桁架转换层能对高层建筑的侧向位移起到约束作用，桁架转换层极易发生位移集中，是高层建筑的脆弱部分，在高层建筑设计时应重点关注桁架转换层设计。

实验将桁架转换层所在楼层中所有竖向构件单元在底部各节点的节点力和表示楼层竖向构件的剪力，竖向构件剪力可表示桁架转换层地震反应规律，表1和表2分别为高层建筑受到X方向和Y方向地震时的总剪力和层间剪力。

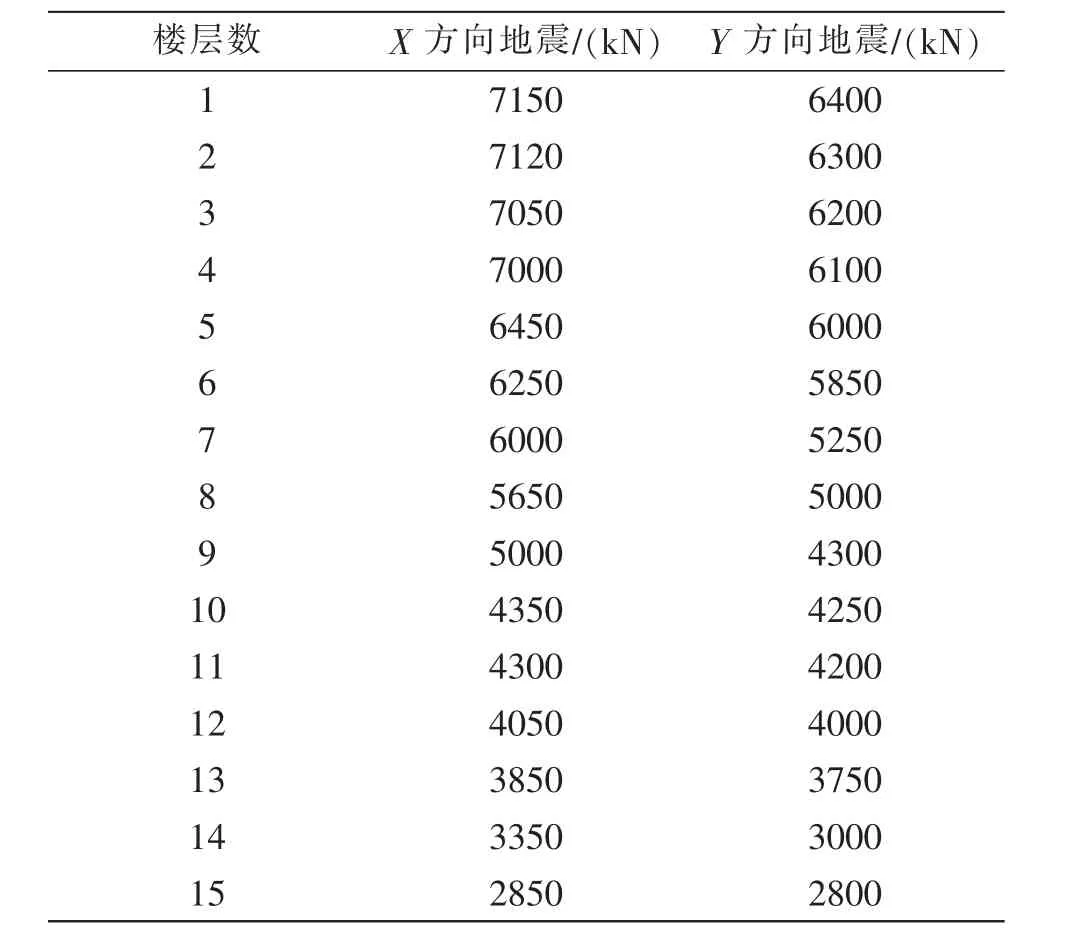
表1 建筑结构总剪力变化 （kN）Table 1 Change of total shear force of building structure （kN）

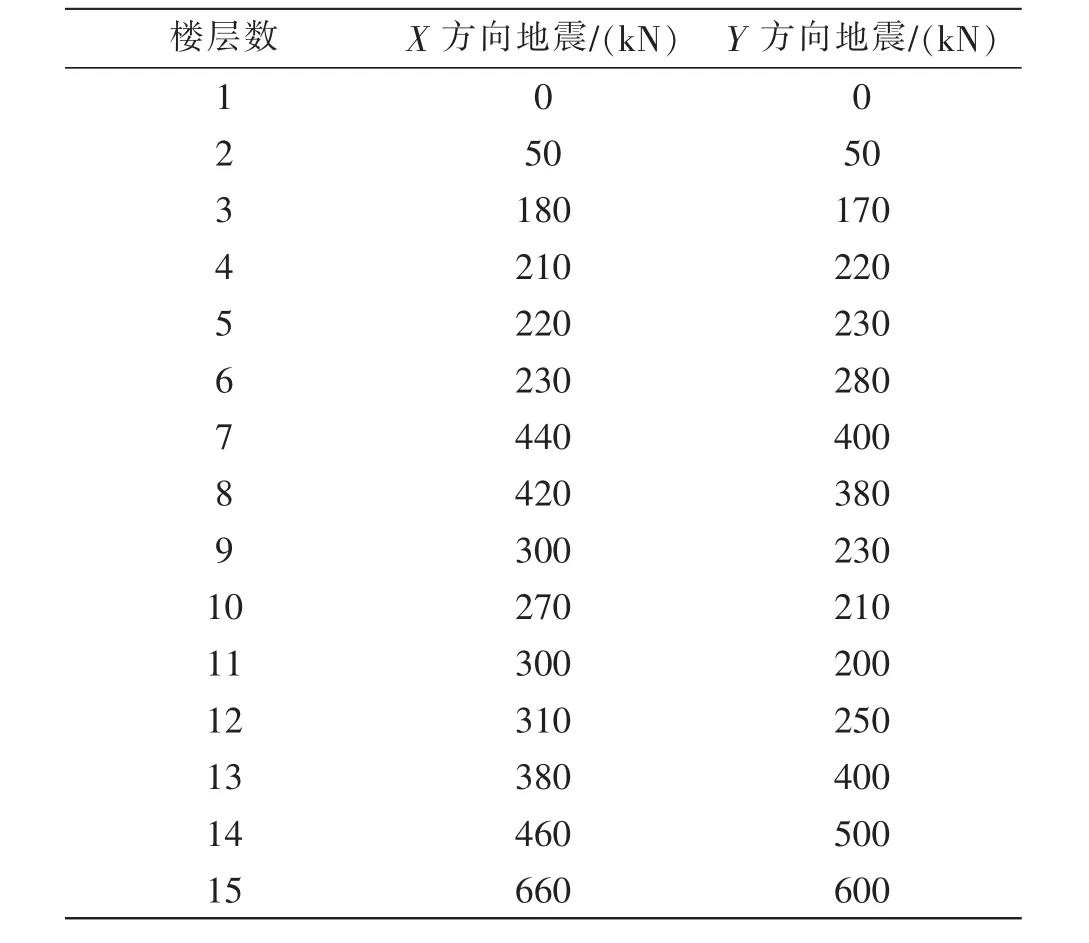
表2 建筑结构层间剪力（kN）Table 2 Inter-storey shear force （kN） of building structure

从表1数据结果可知，高层建筑桁架转换层在X方向和Y方向地震作用下的结构总剪力变化呈现楼层数增加总剪力降低的趋势，且在桁架转换层中剪力发生小幅度突变，剪力增加提升，且从表2数据结果可知，层间剪力在6楼层时发生突变，因为该楼层为桁架转换层，在该楼层时刚度突然发生变化。

2.4 地震反应时程分析

结合该高层建筑施工场地条件，选取三条地震波作为地震动输入荷载，分别为场地波、ELCentro波和规范反应谱拟合的人工地震波，根据建筑抗震规范中对地震加速度时程曲线的最大规定值，以加速度峰值0.17 m/s2对三条地震波实施调幅处理，然后采用本文方法对高层建筑桁架转换层结构进行分析，比较三种地震波作用下轴10和轴11间桁架腹杆节点在Y方向时的位移时程变化，结果如图6所示。

图6 桁架腹杆节点时程位移曲线Fig.6 Time-history displacement curve of truss web link node

从图6可知，人工波地震作用下转换层腹杆节点的位移时程变化均显著高于EL Centro和场地波，且最大时程位移为56.2 mm，而EL Centro和场地波地震波下的最大时程位移分别为和9.2 mm和8.6 mm。从该结果表明，高层建筑桁架转换层受不同类型地震波影响后，桁架腹杆节点均发生较大程度位移，因此需注重桁架高层建筑桁架转换层腹杆节点设计，提升建筑的稳定性。

3 结语

带桁架转换层的高层建筑转换层地震作用时容易出现位移过大现象，导致建筑结构出现危险，因此在进行高层建筑桁架转换层设计时应注重对转换层的加固设计。且根据不同地震波对桁架腹杆节点的位移时程变化影响结果可知，桁架腹杆节点在不同地震波下的位移变化均较大，因此对桁架腹杆节点设计也应重点加强。