二乙基次膦酸铝协同含磷有机硅阻燃PA66热分解动力学

邹梦浩，罗钟琳，乔艺卉，王标兵

(常州大学材料科学与工程学院，江苏常州 213100)

聚酰胺66 (PA66)是一种重要的工程塑料，其具有许多优异的性能，比如较高的拉伸强度，高延展性，低摩擦系数，良好的耐化学药品性、耐磨性和电绝缘性，以及易加工性等[1]。但是纯PA66材料非常易燃并且在燃烧过程中产生大量滴落，因此，其应用领域受到很大的限制。通过加入含磷阻燃剂，如磷酸酯、缩聚磷酸酯、有机膦酸盐等[2]或协效[3]可以有效地提高材料的阻燃性能[4]。

聚合物的燃烧行为在加入阻燃剂后往往会发生改变，其燃烧行为与热分解反应密切相关，研究聚合物及其阻燃复合材料的热分解动力学对理解其热分解行为和分解机理有重要意义[5-7]。宁娟霞等[8]研究了自制含磷氮及磺酸盐集于一体的SNP阻燃剂对聚碳酸酯(PC)热分解影响，通过Kissinger法(K法)和Flynn-Wall-Ozawa法(FWO法)计算，其分解活化能相对纯PC分别降低9.9%和9.0%，而且促进了氮气氛围下的成炭，成炭量增加28%，提高了PC的阻燃性能。对聚合物热分解动力学研究有许多方法，比如K法[9-11]，FWO法[12]，Coats-Redfern法[4，13]和Freeman-Carroll法[14]等。

笔者利用热失重(TG)分析仪研究了阻燃PA66在N2氛围下的热稳定性，采用K法和FWO法计算了阻燃PA66的热分解活化能等参数，并进一步采用Coats-Redfern法研究了材料的热分解动力学函数和机理。

1 实验部分

1.1 主要原料

PA66粒料：Zytel 101L NC010，美国杜邦公司；

二乙基次膦酸铝(AlPi)：OP1240，白色粉末，粒径为10～20 μm，磷质量分数为23%～24%，德国科莱恩公司；

多聚苯磷酰硅油(PPSO)：双羟丙基硅油与苯基磷酰二氯反应产物，透明油状液体，自制。

1.2 主要设备与仪器

密炼机：US-70C型，常州苏研科技有限公司；

TG分析仪：TGA 4000型，英国Perkin Elmer公司。

1.3 试样制备

将PA66粒料、阻燃剂AlPi和PPSO于100℃真空烘箱中干燥12 h，将各组分按照表1配方均匀混合，密炼6～8 min，得到不同阻燃剂含量的阻燃PA66，密炼温度为260℃，转子转速为60 r／min。

表1 阻燃PA66配方 %

1.4 性能测试

对不同升温速率下的阻燃PA66进行TG分析，升温速率为10，20，30，40℃／min，气氛为N2，气体流速为20 mL／min，试样质量为(10.00±0.50) mg，升温区间为30～850℃。

1.5 热分解动力学基础

由非等温动力学方程dα／dt=kf(α)和热力学Arrhenius方程k=Aexp(-E／RT)相互结合并分别通过微分和积分转换变形，可得到热分解动力学Kissinger方程和Flynn-Wall-Ozawa方程，分别如式(1)、式(2)所示：

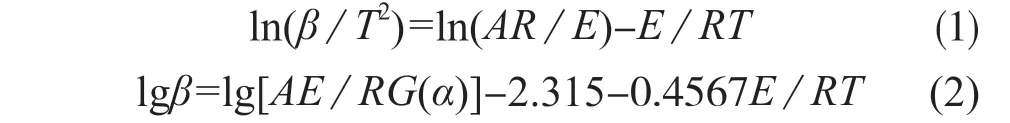
式中：α——分解率；

t——时间；

k——Arrhenius速率常数；

T——温度；

A——指前因子；

β——升温速率；

E——活化能；

R——气体常数，其值为8.314 J／(K·mol)；

f(α)——尚未分解部分的指数函数，与分解率 有关；

G(α)——反应机理函数。

假设2RT／E趋近0，对式(1)和式(2)进行一系列数学变换，得Coats-Redfern方程，如式(3)所示：

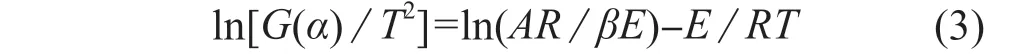
采用三种动力学方法对阻燃PA66进行热分解动力学分析，其中以K法和FWO法作图求得不同分解率下的热分解活化能，以Coats-Redfern法作图计算的热分解活化能与K法和FWO法作比较，确定反应机理函数和反应级数。

2 结果与讨论

2.1 阻燃PA66的热稳定性

图1给出了阻燃PA66在N2氛围下的TG和微商热重(DTG)曲线，升温速率为10℃／min，相关测试数据列于表2。

图1 N2氛围下阻燃PA66的TG和DTG曲线

表2 阻燃PA66的TG测试数据

由图1和表2可以看出，在N2氛围下，纯PA66 (1#试样)的分解为一段分解，初始分解温度(T5%)为413℃。随着AlPi的加入，2#试样的初始分解温度出现了较大幅度的下降，这主要是加入的AlPi受热分解产生的物质会促进PA66基体的分解。与1#试样相比，2#试样和3#试样的热分解均分为两步，第一步热分解时的最大分解速率温度为430℃，这是由于AlPi的热分解与基体发生相互作用，促进基体的分解；第二步热分解时的最大分解速率温度为486℃，这主要是PA66材料骨架的进一步分解。在800℃下，与1#试样的残炭率2.9%相比，2#试样的残炭率仅为5.7%，说明AlPi对PA66的阻燃效果主要是AlPi受热分解，产生较多的可挥发性含磷自由基小分子气相物质，阻止了PA66基体燃烧产生的可燃性气体的链式燃烧反应；部分AlPi受热分解，产生磷酸，在持续高温下继续脱水生成焦磷酸，导致残炭略微升高。随着PPSO的加入，3#试样的初始分解温度并未发生明显的变化，且在N2氛围下的热分解行为未发生明显变化。在N2氛围下，3#试样在800℃下的残炭率(4.5%)低于2#试样的残炭率(5.7%)，这可能归因于AlPi含量的降低[15]。

2.2 阻燃剂对阻燃PA66热分解活化能的影响

图2和图3分别给出了阻燃PA66在不同分解率下lnβ／T2与1 000／T (K法)的关系曲线和lnβ与1 000／T (FWO法)的关系曲线，并对曲线进行最小二乘法非线性拟合，由拟合直线的斜率求得阻燃PA66在不同热分解阶段的热分解活化能和相关系数，数据列于表3和表4。

图2 阻燃PA66在不同分解率下lnβ／T2与1 000／T (K法)的关系曲线

由表3和表4可以看出，各数据的相关系数较高[16]，说明实验数据可靠性较高，K法和FWO法能够用于阻燃PA66的热分解动力学研究。

图3 阻燃PA66在不同分解率下lnβ与1000／T (FWO法)的关系曲线

不同分解率下K法和FWO法的活化能与分解率的关系曲线如图4所示。比较两种方法的计算结果可知，用FWO法计算的活化能和K法的活化能较为接近，两种方法所呈现的趋势一致。热分解活化能在整个分解过程都会发生变化，因此阻燃PA66的热分解无法通过简单过程进行。对于1#试样，随着分解率的升高，活化能的变化较小，基本保持在一个较为稳定的水平；对于2#试样，随着分解率的升高，活化能呈现先减小后增大，然后再减小的趋势，且活化能均小于1#试样，这一现象可归因于AlPi的加入，促进了基体材料的提前分解，导致前期的热分解活化能降低，而在燃烧分解时AlPi主要起到气相阻燃作用，部分AlPi分解产生的含磷自由基与PA66杂化裂解产物发生反应形成次膦酸偶联产物，高温下稳定性较差，进一步分解成以铝离子为交联点的交联物质和磷酸铝、焦磷酸铝的炭状残留物，较多磷酸铝、焦磷酸铝稳定性高的产物的存在导致活化能的增加，在后期以铝离子为交联点的交联物质继续分解，导致活化能降低[17]，所以2#试样的热分解活化能随着分解率的升高呈现先减小后增加，然后再减小的趋势；对于3#试样，在分解率＜0.25时，3#试样的活化能小于1#试样，在分解率≥0.25时，随着分解率的增加，活化能升高。3#试样前期(分解率＜0.25)的活化能偏小，是因为AlPi的加入，促进了基体材料的提前分解，导致前期的热分解活化能低于1#试样，但是当分解率≥0.25时，含磷有机硅阻燃剂PPSO与前期AlPi产生的磷酸类相互作用于基体，在基体表面产生P—Si—C致密交联炭层，对基体有一定的保护作用，导致活化能增大，分解后期，产生的P—Si—C炭层增多，炭层具有较好的稳定性，所以活化能迅速升高。

表3 K法计算的阻燃PA66的热分解活化能及相关系数

表4 FWO法计算的阻燃PA66的热分解活化能及相关系数

图4 不同分解率下K法和FWO法的活化能与分解率的关系曲线

2.3 热分解机理和反应级数

Coats-Redfern法是研究聚合物热分解机理和动力学模型的有效方法[14]。为了研究活化能对分解率的依赖性和在不同机制参与下的复杂反应，选用Coats-Redfern法进一步研究阻燃PA66热分解机理和反应级数。由图4可知，阻燃PA66随着温度的变化有不同的分解过程，根据不同的分解过程，可以从ln[G(α)／T2]与1 000／T的拟合曲线获得直线斜率，计算出活化能。

比较表3和表4可知，K法和FWO法计算的活化能相差较小，基本一致。在整个分解过程(0.10≤α≤0.90)中，1#试样的活化能变化较小，基本不变，采用K法计算的活化能平均值为213.1 kJ／mol，采用FWO法计算的活化能平均值为214.4 kJ／mol。将35个常用动力学机理函数G(α)与不同分解率对应的温度分别代入式(3)并作图拟合求出直线斜率[18]，从而可求得不同升温速率下的热分解活化能。图5是机理函数G(α)=1-(1-α)1／4(0.10≤α≤0.90)时，1#试 样 的ln[G(α)／T2]对1 000／T的拟合曲线，相关数据列于表5。当机理函 数G(α)=1-(1-α)1／4(0.10≤α≤0.90)时，采用Coats-Redfern法计算的不同升温速率下1#试样的热分解活化能平均值为207.9 kJ／mol，与采用K法计算的活化能平均值(213.1 kJ／mol)和FWO法计算的活化能平均值(214.4 kJ／mol)最为接近，所以1#试样为相边界反应分解机理，反应级数为1／4，其分解机理函数G(α)=1-(1-α)1／4(0.10≤α≤0.90)。

图5 1#试样的ln[G(α)／T 2]与1 000／T的拟合曲线

表5 Coats-Redfern法计算的不同升温速率下阻燃PA66对应G(α)的热分解活化能 kJ／mol

对于2#试样，整个分解过程可分为三段，当α≤0.35时，活化能随α的升高慢慢降低，采用K法计算的活化能平均值为188.5 kJ／mol，采用FWO法计算的活化能平均值为190.5 kJ／mol；当0.40≤α≤0.65时，活化能随α的升高基本保持不变，采用K法计算的活化能平均值为165.8 kJ／mol，采用FWO法计算的活化能平均值为169.1 kJ／mol；当α≥0.70时，活化能随α的升高慢慢升高后有所减小，采用K法计算的活化能平均值为188.2 kJ／mol，采用FWO法计算的活化能平均值为190.8 kJ／mol。经Coats-Redfern法获得活化能的计算过程与1#试样一致。其中，图6a为机理函数G(α)=α2(α≤0.35，α≥0.70)时，ln[G(α)／T2]对1 000／T的拟合曲线，相关数据列于表5。当机理函数G(α)=α2(α≤0.35，α≥0.70)时，采用Coats-Redfern法计算不同升温速率下2#试样的热分解活化能平均值为206.8 kJ／mol，与2#试样采用K法计算的活化能平均值[188.5 kJ／mol (α≤0.35)，188.2 kJ／mol (α≥0.70)]和FWO法计算的活化能平均值[190.5 kJ／mol (α≤0.35)，190.8 kJ／mol (α≥0.70)]最为接近；图6b为机理函数G(α)= α3／2(0.40≤α≤0.65)时，ln[G(α)／T2]对1 000／T的拟合曲线，当机理函数G(α)=α3／2(0.40≤α≤0.65)时，采用Coats-Redfern法计算的不同升温速率下2#试样的热分解活化能平均值为157.5 kJ／mol，与2#试样采用K法计算的活化能平均值(165.8 kJ／mol (0.40≤α≤0.65)和FWO法计算的活化能平均值[169.1 kJ／mol (0.40≤α≤0.65)]最为接近。所以2#试样在分解率α≤0.35和α≥0.70时，分解机理函数G(α)=α2，反应级数为2；在0.40≤α≤0.65时，分解机理函数G(α)=α3／2，反应级数为3／2。在整个分解阶段均属于相边界反应分解机理。

图6 2#试样的ln[G(α)／T 2]与1 000／T的拟合曲线

对于3#试样，整个分解过程可分为两段，当α≤0.50时，活化能随α的升高缓慢增加，采用K法计算的活化能平均值为216.7 kJ／mol，采用FWO法计算的活化能平均值为217.1 kJ／mol；当α≥0.50时，活化能随α的升高迅速增大，采用K法计算的活化能平均值为360.7 kJ／mol，采用FWO法计算的活化能平均值为354.8 kJ／mol。采用Coats-Redfern法获得活化能的计算过程与1#试样一致。其中，图7a为机理函数G(α)=α+(1-α)ln(1-α) (α≤0.5)时，ln[G(α)／T2]对1 000／T的拟合曲线，经过计算，当机理函数G(α)=α+(1-α)ln(1-α) (α≤0.50)时，采用Coats-Redfern法计算的不同升温速率下3#试样的热分解活化能平均值为218.9 kJ／mol，与3#试样采用K法计算的活化能平均值[216.7 kJ／mol (α≤0.50)]和采用FWO法计算的活化能平均值[217.1 kJ／mol (α≤0.50)]最为接近；图7b为机理函数G(α)=[-ln(1-α)]3(α≥0.5)时，ln[G(α)／T2]对1 000／T的 拟 合 曲 线，当G(α)=[-ln(1-α)]3(α≥0.50)时，采用Coats-Redfern法计算的不同升温速率下3#试样的热分解活化能平均值为428.9 kJ／mol，与3#试样采用K法计算的活化能平均值[360.7 kJ／mol (α≥0.50)]和采用FWO法计算的活化能平均值[354.8 kJ／mol (α≥0.50)]最为接近。所以3#试样在α≤0.50为二维扩散的分解机理，反应级数为1，其分解机理函数G(α)=α+(1-α)ln(1-α)；在α≥0.50时为随机成核和随后生长分解机理，反应级数为3，其分解机理函数G(α)= [-ln(1-α)]3。

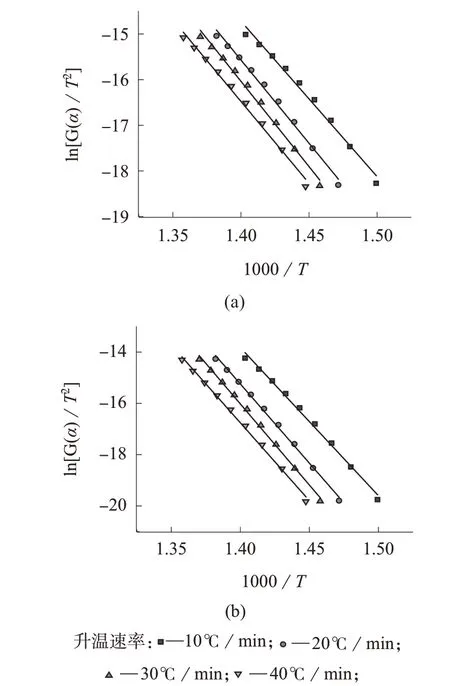
图7 3#试样的ln[G(α)／T 2]对1 000／T的拟合曲线

3 结论

对于PA66基体，阻燃剂AlPi与PPSO之间存在协效阻燃作用，TG分析表明，阻燃剂的加入，降低了阻燃PA66的初始分解温度，材料的热分解行为也发生了改变；经计算拟合，K法和FWO法较适用于分析热分解过程的活化能的变化，Coats-Redfern法能很好地推测出材料的分解机理及其方程，1#试样的机理函数G(α)=1-(1-α)1／4(0.10≤α≤0.90)，反应级数为1／4，分解机理为相边界反应分解机理；2#试样的机理函数G(α)=α2(α≤0.35，α≥0.70)和G(α)=α3／2(0.40≤α≤0.65)，反应级数分别为2和3／2，整个分解过程均为相边界反应分解机理；3#试样的机理函数G(α)=α+(1-α)ln(1-α)(α≤0.50)和G(α)=[-ln(1-α)]3(α≥0.50)，反应级数分别为1和3，分解机理分别为二维扩散的分解机理、随机成核和随后生长分解机理。