一节优质决赛课的欣赏与思考

李定平

【摘要】优质课决赛是同一课题《两角差的余弦公式》，对优胜者的教学过程进行了介绍与评述，基于数学学科核心素养下对本课教学内容所蕴含的育人教育价值提出了不同的教学设计，即“问题引领，自主建构”的“问题串”教学设计，在问题解决的过程中发展学生的核心素养。

【关键词】优质决赛课;教学设计;问题串

佛山市顺德区高中数优质课决赛是两位老师执教同一课题《两角差的余弦公式》，笔者有幸听了他们的课，其中，碧桂园学校国际课程熊晓敏老师的课让笔者很有感想，下面分享笔者的心得，以飨同行。

一、流程简单，却憾动人

熊老师的课没有挖掘什么教材内涵，也没有补充什么综合题、高考题，教学流程非常简洁，效果却非常好，教学过程如下：

1.课题引入

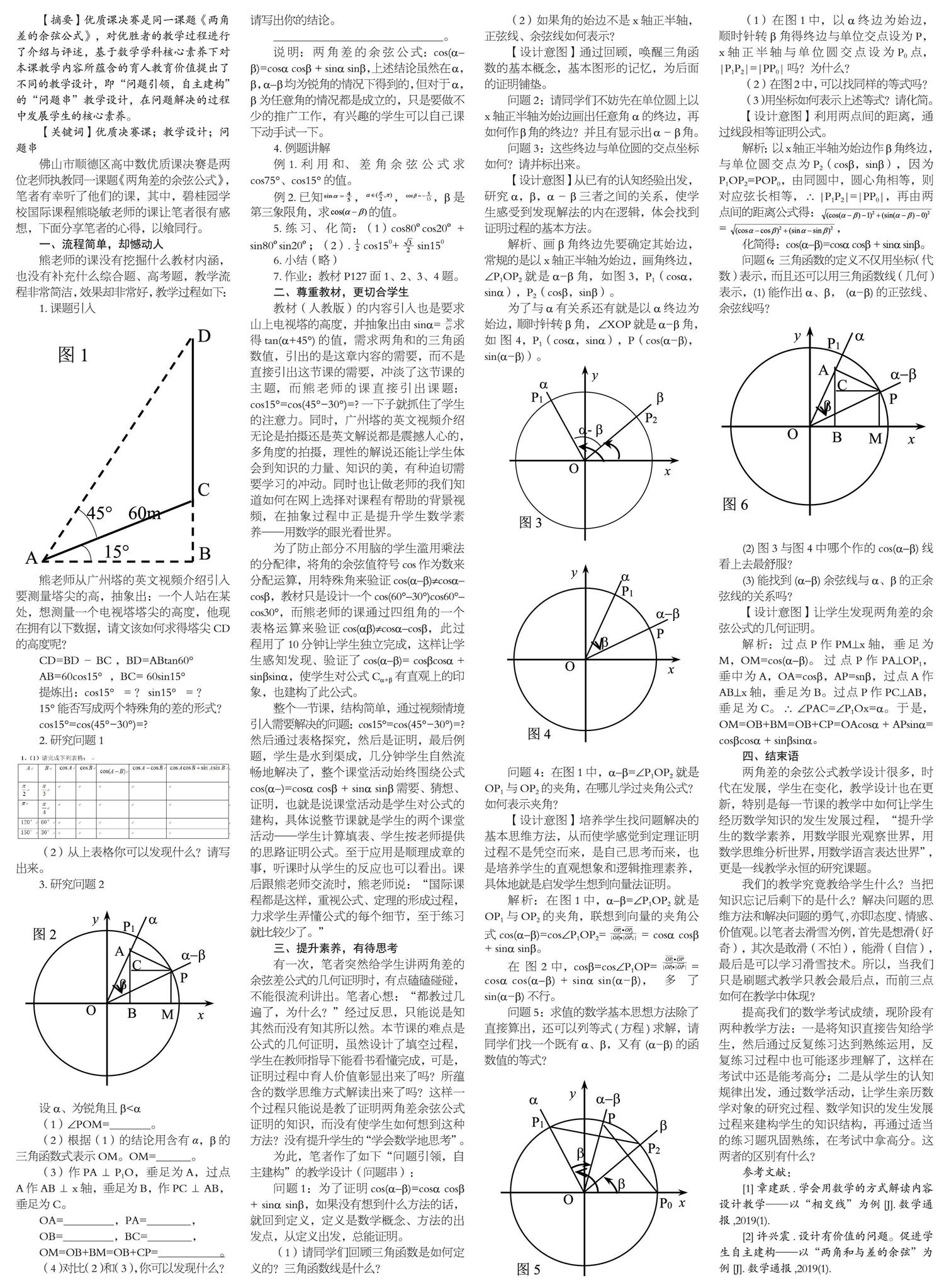
熊老师从广州塔的英文视频介绍引入要测量塔尖的高，抽象出：一个人站在某处，想测量一个电视塔塔尖的高度，他现在拥有以下数据，请文该如何求得塔尖CD的高度呢？

CD=BD-BC ，BD=ABtan60°

AB=60cos15°，BC= 60sin15°

提炼出：cos15°=？sin15°=？

15°能否写成两个特殊角的差的形式？

cos15°=cos（45°-30°）=？

2.研究问题1

（2）从上表格你可以发现什么？请写出来。

3.研究问题2

设α、为锐角且β<α

（1）∠POM=             。

（2）根据（1）的结论用含有α，β的三角函数式表示OM。OM=           。

（3）作PA⊥P1O，垂足为A，过点A作AB⊥x轴，垂足为B，作PC⊥AB，垂足为C。

OA=                ，PA=              ，

OB=                ，BC=              ，

OM=OB+BM=OB+CP=                     。

（4）对比（2）和（3），你可以发现什么？请写出你的结论。

。

说明：两角差的余弦公式：cos（α?β）=cosα cosβ + sinα sinβ，上述结论虽然在α，β，α?β均为锐角的情况下得到的，但对于α，β为任意角的情况都是成立的，只是要做不少的推广工作，有兴趣的学生可以自己课下动手试一下。

4.例题讲解

例1.利用和、差角余弦公式求cos75°、cos15°的值。

例2.已知，，，β是第三象限角，求的值。

5.练习、化简：（1）cos80?cos20? + sin80?sin20?;（2）.cos150+sin150

6.小结（略）

7.作业：教材P127面1、2、3、4题。

二、尊重教材，更切合学生

教材（人教版）的内容引入也是要求山上电视塔的高度，并抽象出由sinα=求得tan（α+45°）的值，需求两角和的三角函数值，引出的是这章内容的需要，而不是直接引出这节课的需要，冲淡了这节课的主题，而熊老师的课直接引出课题：cos15°=cos（45°-30°）=？一下子就抓住了学生的注意力。同时，广州塔的英文视频介绍无论是拍摄还是英文解说都是震撼人心的，多角度的拍摄，理性的解说还能让学生体会到知识的力量、知识的美，有种迫切需要学习的冲动。同时也让做老师的我们知道如何在网上选择对课程有帮助的背景视频，在抽象过程中正是提升学生数学素养——用数学的眼光看世界。

为了防止部分不用脑的学生滥用乘法的分配律，将角的余弦值符号cos作为数来分配运算，用特殊角来验证cos（α?β）≠cosα?cosβ，教材只是设计一个cos（60°?30°）cos60°?cos30°，而熊老师的课通过四组角的一个表格运算来验证cos（αβ）≠cosα?cosβ，此过程用了10分钟让学生独立完成，这样让学生感知发现、验证了cos（α?β）= cosβcosα + sinβsinα，使学生对公式Cα+β有直观上的印象，也建构了此公式。

整个一节课，结构简单，通过视频情境引入需要解决的问题：cos15°=cos（45°-30°）=？然后通过表格探究，然后是证明，最后例题，学生是水到渠成，几分钟学生自然流畅地解决了，整个课堂活动始终围绕公式cos（α?）=cosα cosβ + sinα sinβ需要、猜想、证明，也就是说课堂活动是学生对公式的建构，具体说整节课就是学生的两个课堂活动——学生计算填表、学生按老师提供的思路证明公式。至于应用是顺理成章的事，聽课时从学生的反应也可以看出。课后跟熊老师交流时，熊老师说：“国际课程都是这样，重视公式、定理的形成过程，力求学生弄懂公式的每个细节，至于练习就比较少了。”

三、提升素养，有待思考

有一次，笔者突然给学生讲两角差的余弦差公式的几何证明时，有点磕磕碰碰，不能很流利讲出。笔者心想：“都教过几遍了，为什么？”经过反思，只能说是知其然而没有知其所以然。本节课的难点是公式的几何证明，虽然设计了填空过程，学生在教师指导下能看书看懂完成，可是，证明过程中育人价值彰显出来了吗？所蕴含的数学思维方式解读出来了吗？这样一个过程只能说是教了证明两角差余弦公式证明的知识，而没有使学生如何想到这种方法？没有提升学生的“学会数学地思考”。