以有效习题设计提高转化能力的策略探究


摘 要:转化是小学数学学习中常用的策略,根据从已知到未知,从简单到复杂,可以使问题化繁为简,化难为易。本文从有效习题设计的角度,浅谈转化的一般策略。
關键词:转化;化繁为简;化新为陈;数形结合;化隐为显;等量变化
一、 在练习中感知转化的一般规则
(一)化繁为简
在解决问题的过程,利用转化的策略可以将较为复杂的问题转化为简单的问题,从而获得解决复杂问题的基本思路。学生在学习简便运算时就是运用的化繁为简的转化规则。
【习题1】计算下面各题,怎样简便怎样算。
(1)75×1.25+12×1.25+13×1.25
(2)34+29+79
【说明】第(1)题可以运用乘法分配律,将较为复杂的小数乘法计算转化为100×1.25这样整百数乘小数的计算。第(2)题利用加法结合律,变为计算34+29+79,从而将原题转化为分数加整数的计算。这两题从计算的角度而言都属于旧知,但是都采用了转化的策略,将复杂的问题转化成简单的问题,从而帮助学生从数学思想方法上再度认识简便运算。
(二)化新为陈
学生在学习过程中面对全新的知识,需要一定的基础知识储备和基本经验准备,这些基础知识、基本经验的积累是学生探究新问题的基础。在教学中,要引导学生将陌生的新问题尽可能转化成熟悉的旧问题,帮助问题的解决。
【习题2】11. 求涂色部分的面积。(单位:cm)
【说明】此题是练习十六第11题。两小题中涂色部分都是不规则的图形,涂色部分的形状显然不是学生熟识的,其面积的计算方法对学生而言是个全新的问题。解决此类问题要指导学生尽量将全新的、不规则的图形转化为熟悉的、规则的平面图形,这也是转化策略的基本思想。在本题中,根据观察可见,第1小题可将左右两侧的半圆通过旋转运动至图中空白部分,从而将涂色部分的面积转化为边长是4厘米的正方形的面积。第2小题图中的左下方的涂色部分可以通过旋转至右上方,从而将涂色部分面积转化为底和高都是12厘米的直角三角形的面积。
(三)数形结合
数学家华罗庚指出:“数缺形时少直观,形缺数时难入微。”在研究数学问题时,由数想形,由形思数,数和形之间的相互转化、相互依托,常常会打开数学研究的新局面。教师在教学中要引导学生通过数与形的转化,发现数学本质。
【习题3】7. (1)观察下面每个图形中圆的排列规律,并填空。
1=1×1
1+3=4=2×2
1+3+5=9=3×()
1+3+5+7=()=()×()
(2)根据上面的规律用简便方法计算。
1+3+5+7+9+11
1+3+5+7+9+11+13+15+17+19
【说明】此题是教材练习十六第7题,观察每个图形中的排列规律,圆的个数总和既可以看成是从1开始的连续个奇数相加,也可以看成是正方形边长与边长的乘积(边长的平方)。引导学生将图和算式进行比较,发现加法算式中加数一共有几个,正方形的边长就是几;而连加算式的结果就是正方形边长的平方。在数形结合的基础上寻找出规律后再解决第(2)小题的简便计算,学生就易于理解了。关于圆的排列规律还不致如此,如果教师放手请学生观察2×2、3×3、4×4的三幅点阵图,还能发现如下规律,从而丰富学生对转化策略的理解。
2×2=1+2+1
3×3=1+2+3+2+1
4×4=1+2+3+4+3+2+1
(四)化隐为显
在解决问题的过程中,有时看似解决问题的条件不具备,其实往往是呈隐形状态,如果能根据已有条件,寻找出必要的隐形条件,问题就迎刃而解了。
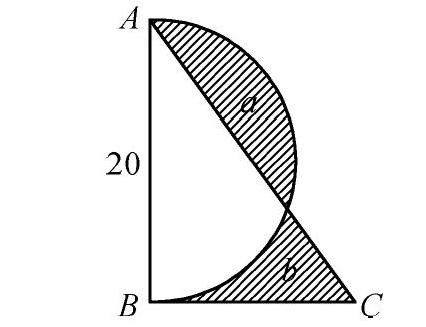
【习题4】如图,三角形ABC是一个直角三角形,已知阴影部分b的面积比阴影部分a少23平方厘米,求BC的长是多少?
【说明】初读题目,觉得此题中BC的长度难以求得,因为三角形ABC的面积未知。仔细分析已知条件,结合图示,根据条件“阴影部分b的面积比阴影部分a少23平方厘米”,不难发现由于半圆和三角形重叠,都有共有的部分即图中空白部分,所以三角形ABC的面积比半圆少23平方厘米。寻找到这个必要的隐藏条件,问题就迎刃而解了,只需要计算出半圆的面积是π×102÷2=157(平方厘米),就可以求出三角形
ABC的面积是157-23=134(平方厘米),故而BC的长为134×2÷20=13.4(厘米)。学生在今后的学习中经常会遇到隐藏条件的问题,如表面积的变化、体积的变化中,故而化隐为显的转化策略对学生今后的学习也起着非常重要的作用。
二、 在运用中形成转化策略
(一)遵循等量变化的转化原则
转化策略的运用十分广泛,无论是计算、图形还是解决问题中都会运用到。在转化的过程要引导学生认识到在具体转化的过程中,只有等量的转化,才能达到化繁为简、化难为易的目的。
【习题5】2. 用分数表示各图中的涂色部分。
【说明】此题是教材练习十六的第2题,题中的涂色部分通过适当的分割,用平移或旋转的方式进行转化,就可以看出涂色部分与图形整体之间的关系,进而用分数来表示。此题转化的关键就是图形的某些部分在进行平移和旋转前后,大小不能发生变化,进行等量的转化。第三幅图,学生比较容易将整个涂色部分的正方形进行旋转,从而得到916,就是没有进行等量间的转化造成的错误。
【习题6】有三堆围棋子,每堆24枚。第一堆里的黑子数与第二堆里的白子数一样多,第三堆的一半都是白子。这三堆围棋子中白子共有多少枚?
【说明】分析题意,不难发现,因为“第一堆棋子里的黑子数与第二堆棋子里的白子数一样多”,所以第一、第二堆的白子合起来就是24枚,而第三堆白子为24÷2=12(枚),所以三堆一共有24+12=36(枚)白棋子。也可以结合画图(如下图)进行分析,要解决这个问题也是在等量变化的基础上,将第一堆的黑子转化为第二堆的白子,故而,等量变化是转化的必须遵守的原则。
一:
二:
三:
(二)巧用分解和组合
在解决问题的过程中,常常需要将复杂的问题分解为若干个简单的小问题逐一突破,有时也需要寻找问题间的联系,将问题重组。根据具体的问题灵活的使用分解和组合,也是进行转化的常用方法。
【习题7】
12. 光明小学有一个花坛(如下图)。图中正方形的边长为10米,正方形的顶点正好是四个圆的圆心,圆的半径是3米。
【说明】解决这个问题,先要根据要求将图形进行分解,花坛的面积是中间正方形面积和4个34圆面积的和。将四角4个的34圆进行组合,转化为3个整圆的面积,再与正方形面积相加,求出花坛的面积。解决问题的过程中有分到合,充分体现了学生灵活使用转化策略的能力。
(三)善用题组对比
【习题8】明明、东东和为学校同一块长方形草坪设计了不同的行走方案。其中灰色直条都是宽为1米的小路,你能比较一下三个设计方案中草地的面积相等吗?
【说明】通过观察发现将明明设计方案中的小路向左、向下平移就可以转化成东东的设计方案,所以明明和东东设计方案中小路的面积是相等的,草地的面积也是相等的。但是丁丁设计方案中有一条小路的形状是平行四边形,所以丁丁设计方案的小路面积和其他两人不等,草地的面积也就不相等了。通过这样的题组练习,学生对于转化过程中的等量变化理解的就更深刻了。
作者简介:章春玮,江苏省苏州市,苏州市沧浪实验小学校。

