融合工业大数据的热轧厚板轧制力模型研究

章顺虎，姜兴睿，尤凤翔，李寅雪

（苏州大学a.沙钢钢铁学院；b.机电工程学院，江苏 苏州 215021）

在轧制生产中，轧制力是过程控制最为重要的工艺参数。精准的轧制力预测是保证板带材尺寸精度与产品质量的前提条件。预测轧制力的方法主要有理论解析、有限元模拟、人工神经网络预测等几种方法。早在1954 年，Sims[1]就曾在奥罗万方程的基础上提出了一种预测轧制力的解析模型，并导出了轧件前、后滑区上的平均单位压力公式。该模型应用广泛，结构简单，但由于采用了较多简化，因而预测精度不高。1973 年，小林史郎[2]提出了一种求解三维轧制总功率泛函的积分框架，但碍于被积函数的非线性，仅通过计算机获得了数值结果。随后，Kato 等[3]在1980 年也提出了一个加权速度场，但同样没能获得解析解。Freshwater[4]在经典平轧理论的基础上，提出了均匀变形和非均匀变形条件下轧制力的简化计算公式。2012 年，赵德文等[5]率先提出采用应用应变矢量内积法和共线矢量内积法分析简化的二维流函数，获得了轧制力及轧制力矩的解析模型。此后，章顺虎等[6]提出将轧制变形渗透率引入厚板轧制过程，并对速度场进行了修正，获得了更为精确的结果，最近，又根据厚板轧制特性提出了厚板轧制的二维椭圆形速度场[7]，成功获得了轧制力能参数的解析解。以上依赖传统解法获得的模型，其优势在于可以提供各种参数的显示表达式，直观反映各种物理量的函数制约关系。然而，由于在对轧制过程分析时不得不采用多个假设或简化，预测精度存在较大偏差，难以满足高精度的生产控制需要。

随着人工神经网络（ANN）和大数据技术的发展，利用二者互补预测轧制力成为未来的一个方向。人工神经网络的优势在于无论是多么复杂的轧制工艺，只要有足够多的数据样本，就可以建立神经网络来进行预测[8]。为了解决传统方法预测连轧机组中第一组的轧制力存在较大误差的问题，Duckman 与Yongsug[9]训练了一个神经网络来预测第一组轧制力，该模型对轧制力的预测效果较好，减小了带钢前端的厚度误差。Dixit 与Chandra[10]使用了BP 神经网络对轧制力和轧制力矩的上下界进行了预测，发现模型训练集和测试集的精度达到一定程度后就不再增加。Son 等[11]为了提高热轧机轧制力的预测精度，提出融合神经网络和遗传算法的轧制力模型，其后，他们又提出了一种可以用于长期学习和短期学习的在线学习神经网络[12]，结果表明，在线学习神经网络预测的轧制力与实际轧制力非常接近，大大减小了带钢厚度误差。Moussaoui 等[13]采用了 Matlab 中的贝叶斯证据（Bayesian Evidence）训练函数实现了轧制力的预测，并与传统的经验公式结果进行了对比。结果表明，该方法对实际轧机数据具有较平滑的拟合效果。Ghaisari 等[14]开发了一种基于人工神经网络的智能间接检测方法，实现了对产品力学性能的监测。该智能系统的输入项包括各个生产阶段的多种参数，可以预测屈服强度、极限抗拉强度和伸长率等性能。Bagheripoor 与Bisadi[15]评估了具有不同隐含层结构的神经网络，优化出了能够准确预测轧制力的神经网络模型。Guo 等[16]建立了有限元与人工神经网络相结合的镁合金板热轧轧制力预测模型，并用有限元模拟对预测模型进行了综合验证。所建立的神经网络模型适用于镁合金板热轧过程的在线控制和轧制规程优化。何亚元[17]使用数学模型和BP 神经网络相结合的方法构建了CSP 生产线轧制力预测模型。尽管如此，已有关于神经网络预测轧制力的研究由于数据规模不大，因而泛化能力差，并且这些模型都是黑箱模型，无法呈现输入-输出参量的函数映射关系，很难被生产现场所采用。

为了获得可靠实用的轧制力模型，文中利用工业大数据进行神经网络建模，并利用其结果对前期建立的理论模型进行误差补偿，获得二者相互补充的整合模型。通过与实测值进行对比，揭示理论模型、神经网络模型以及整合模型的精度情况。

1 已有理论模型

笔者前期提出了描述厚板轧制的椭圆速度场，并以比塑性功率取代法获得了该速度场上轧制能率的解析式[7]：

式中：Φ为轧制总功率；σs为屈服应力，η为轧件入口厚度与出口厚度的比值；m为摩擦因数；k为剪切屈服强度；l为变形区长度；Δh为压下量；b为板宽；vR为轧辊转速；R为轧辊半径，θ为变形区所占轧辊角度；an为中性角；hm为轧件平均厚度；U为变形区秒流量。

通过式（1），可按式（2）分别计算轧制力矩、轧制力以及应力状态系数：

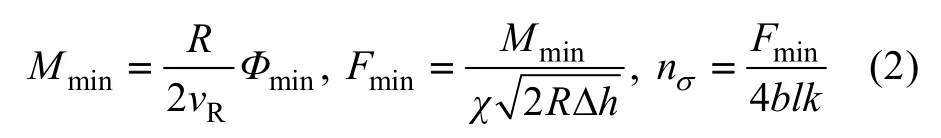
式中：力臂参数χ可以参考文献[18]，一般对于热轧大取0.5，冷轧取0.45。

该模型已成功用于轧制力与轧制力矩的预测，然而，由于推导过程中采用了不少假定和简化，其预测精度还不能控制在10%以下，尚有提升的空间。

2 基于大数据的神经网络建模

2.1 样本数据预处理

从实际生产数据中选取了1213 组数据用来训练神经网络，所有数据均来自国内某厂的Q345 钢的实际轧制数据。采用Matlab 软件构建BP 神经网络：输入层包括5 个参量，依次为板厚h0、压下率r、温度T、轧辊线速度vR以及板宽b，输出层为轧制力P与轧制力矩M。该网络的结构如图1 所示。

图1 BP 神经网络结构Fig.1 Structure of BP neural network

所有输入的数据被分为训练集（train set）、验证集（validation set）以及测试集（test set），每个数据集的占比为0.7∶0.15∶0.15。训练集用于模型拟合，验证集用于初步评估模型的能力并调整模型的参数，测试集用于最终评估模型的泛化能力。

在训练之前，需要将数据进行归一化处理。所有输入和输出数据被缩小或放大到[0，1]这个范围，以符合S 形函数的值域范围。这一步骤保证了所有参量都具有相同的重要程度，同时可以减少网络的训练时间。文中采用的归一化的算法为：

式中：xi表示经过归一化处理后的数据；x为原始数据；xmin为所有x的最小值；xmax为所有x的最大值。

神经网络训练迭代次数最大值设为1000，训练目标为1×10-3，学习率为0.01。采用的训练函数是Matlab 工具箱中的拟牛顿法（BFGS Quasi-Newton）。

2.2 神经网络模型建立与分析

神经网络模型需要确定神经网络的结构形式，包括确定网络层数和各层网络节点数，主要是确定隐含层及其神经元的数量。网络的好坏可以用相关系数R（correlation coefficient）来评判，它的平方为：

在Matlab 中，可以直接在神经网络结果中查看每一个集的R值。文中从单隐含层开始，通过逐步增长法寻找最高R值的神经元组合。通过不断测试，最终确定第一隐含层神经元个数为7，第二层隐含层神经元个数也为7。该模型训练迭代次数为121，该组合的每个集合与总体的R值如图2 所示。

由图2 可见，此时训练集、验证集、测试集上的R值以及总的R值均很高，表明神经网络模型对实际数据具有很高的逼近程度。另外，获得了该模型的误差分布直方图，如图3 所示。

图3 中，横轴为目标值与输出值的差值，即误差；纵轴为1213 组数据在各误差程度区间的分布数量。可以看出，大部分数据的误差都集中在一个较小的范围，误差较大的数据很少。综上可见，文中建立的神经网络模型的预测精度很高，可以实现轧制力、轧制力矩的精确预测。

为评估模型的泛化能力，文中选取了另外一组轧制数据对已构建的神经网络模型进行了分析。选取的轧制数据来自国内某厂现场数据，连铸坯尺寸为320 mm×3470 mm×2000 mm，轧辊直径为1120 mm。经过第一道次的整形轧制后，厚度为299.36 mm，然后转钢90°进行展宽轧制。表1 为第2 道次至第6 道次的轧制数据。

根据式（1）与式（2），可以通过理论模型计算出表1 中的理论轧制力PT与轧制力矩MT，其中采用的变形抗力模型见式（5）。

式中：ε为等效应变；ε˙为等效应变速率；t为轧制温度；T为热力学温度。

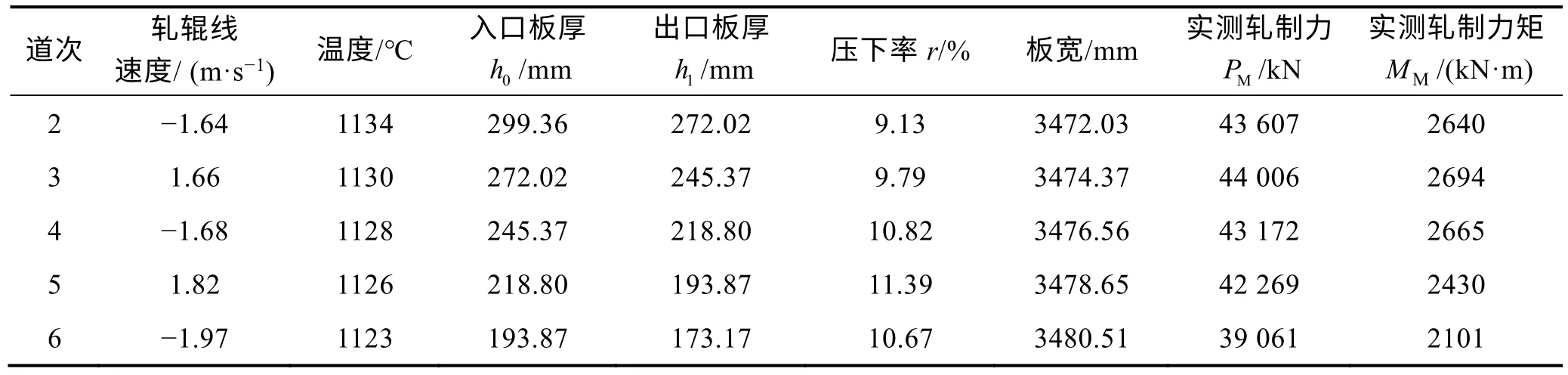
表1 实测轧制参数Tab.1 Measured rolling parameters

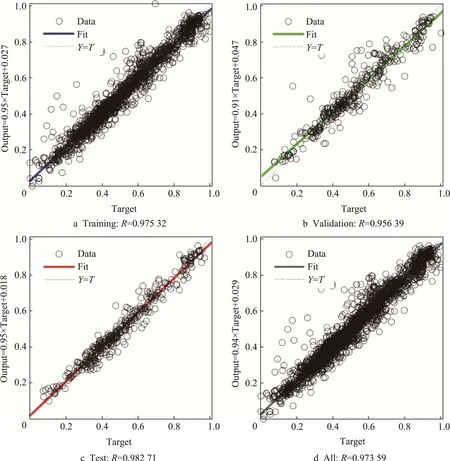
图2 神经网络各数据集的预测精度Fig.2 Prediction accuracy of each data set of the neural network

图3 误差分布直方图Fig.3 Histogram of error distribution

同时，将数据代入神经网络模型中进行计算，获得了神经网络预测轧制力PANN与轧制力矩MANN。以上两种模型的计算结果如表2 所示，其中TPε表达式为；εPANN表达式为。

如表2 所示，理论模型和神经网络模型都可以给出较为合理的结果。其中，理论轧制力平均误差为，轧制力矩平均误差为；神经网络轧制力平均误差，轧制力矩平均误差为。可以看出，神经网络预测值相对于理论计算值更加精确。

2.3 整合模型的构建与讨论

由2.2 节分析可知，虽然神经网络模型的精度高于理论模型，但神经网络模型无法呈现输入-输出参数间的函数制约关系，因此，文中提出利用神经网络模型对理论模型进行修正，融合构造出优势互补的整合模型。该模型融合的基本思想是以理论模型预测轧制力的主值，以大数据模型预测轧制力的偏差，按照偏差补偿的原则把两者整合起来，作为轧制力的预测值，即：

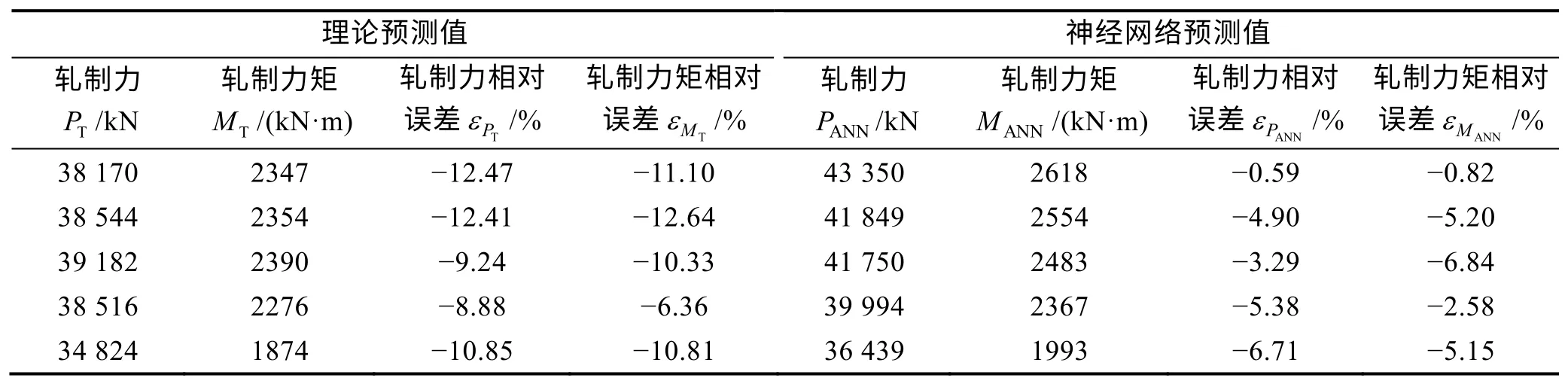
表2 理论与神经网络对轧制力、轧制力矩的预测值与实测值误差Tab.2 Rolling force and rolling torque between theoretical model and neural network prediction and the errors with measured data

式中：δPANN=PM-PANN，δPT=PM-PT，称为轧制力平均误差；δPd为理论模型与神经网络模型误差的间距；δMT与δMANN为神经网络与理论轧制力矩平均误差；δMd为理论与神经网络轧制力矩误差的间距。这种模型融合方法称为加法补偿，原理示意图如图4 所示。

图4 神经网络误差补偿原理Fig.4 Schematic diagram of neural network error compensation principle

根据式（2），可得误差补偿后的轧制力矩与轧制力表达式见式（7）。

根据表1 的轧制参数，计算可得δPANN的均值为-1747 kN，δPT的均值为-4576 kN，故而δPd=2829 kN，同理可得δMd=155 kN · m，因此，经过整合后的轧制力、轧制力矩以及其误差如表3 所示。

表3 整合模型预测轧制力与轧制力矩Tab.3 Prediction of rolling force and rolling torque of the integrated model

对轧制力与轧制力矩的实测值、理论计算值、神经网络预测值以及整合模型计算值进行对比，如图5和6 所示。可以看出，整合模型的轧制力、轧制力矩显著优于理论模型。神经网络预测值在第一道次时较高，但之后下降较快。当道次数大于3 时，整合模型更加接近实测值，预测结果更为稳定。

图5 轧制力对比Fig.5 Comparisons of rolling force

图6 轧制力矩对比Fig.6 Comparisons of rolling torque

3 结论

1）对1213 组轧制数据进行预处理，选用BP 神经网络构建轧制力的预测模型，获得了输入层、隐含层、输出层神经元数以5-7-7-2 的组合形式。该神经网络模型的相关系数R值为0.973 59，可以精确预测轧制力与轧制力矩。

2）通过对比理论模型、神经网络模型以及实测值，表明提出的神经网络模型预测的轧制力精度为-4.17%，轧制力矩预测精度为-4.12%，优于理论模型的轧制力预测精度-10.77%和轧制力矩的预测精度-10.25%。

3）提出了融合两类模型的误差补偿方法，获得了轧制力的整合模型。经计算，该整合模型的轧制力平均误差为-4.09%，轧制力矩平均误差为-4.01%，优于理论模型与神经网络模型的预测值。