新型犹豫不确定Z-Numbers熵及其多准则群决策分析

邹 斌

(安徽广播电视大学 文法与教育学院，安徽 合肥 230022)

为处理模糊信息，Zadeh[1]提出了模糊集理论。在考虑决策问题[2]、模式识别[3]以及模糊推理时[4]，模糊集都是非常有用的工具。然而单凭模糊集中的隶属度无法精确的描述信息。在解决非隶属度的不确定性问题上，Atanassov[5]介绍了直觉模糊集，并应用到多准则决策问题中[6]。犹豫模糊集作为传统模糊集的拓展，这个概念首次被Torra和Narukawa提出[7]。允许元素的隶属度是几个可能值的集合，但这些经典模糊集提出的决策信息的可靠性存在一定的局限性[8]。因此，Zadeh提出了一种新的模糊集理论Z-Numbers。Z-Numbers是一个有序的模糊数对，Z=(A,B)是由两个简单的结构组成，即约束A和可靠性B。

考虑到Z-Numbers的广泛适用性及语言模型的有效性，本文讨论Z-Numbers的一个特殊分支犹豫不确定语言型Z-Numbers。使用一个区间语言值来描述模糊限制比使用单一的语言值更加合适，因为在现实中由决策者提供的语言限制也就是Z-Numbers的第一部分，决策者通常会在几种可能的语言值之间波动。

因而一些连续或离散的语言术语可用来描述这种犹豫性，HULZNs有效地展现这种不完全信息，更充分地表示决策信息。在找到能够完整有效的表示语言信息的模糊数对还无法据此作出最终的决策，本文给出了一种新的语言尺度函数用于度量HULZNs。

文献[9]把交叉熵应用于区间二型模糊集上，为改进距离相似度公式的缺陷提出了对称交叉熵。本文针对犹豫不确定语言型Z-Numbers，提出犹豫不确定语言型Z-Numbers的熵。在处理多准则群决策问题[10]时，首先，从文献[11]关于Z-Number的公理化定义出发，构造一种语言尺度函数；其次，在语言尺度函数基础上，构造犹豫不确定语言型Z-Numbers的熵，建立决策者权重与准则权重的模型，通过排序公式得出最优方案；最后，通过一个算例与文献[12]作比较，说明该决策步骤的有效性和可行性。

1 基本概念

这部分内容主要介绍语言型集合，不确定语言变量，语言尺度函数及其性质，犹豫不确定语言型Z-Numbers的概念及运算。

1.1 语言型集合[12]

1.2 不确定语言变量[12]

1.3 语言尺度函数

本节将介绍两种量化语言的尺度函数。尺度函数能够直观有效地将语言转化为确定的数值，是运用模型作出决策的基础。

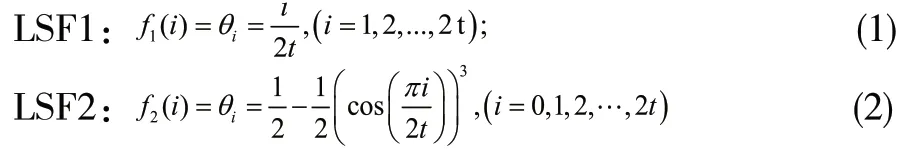
例：令

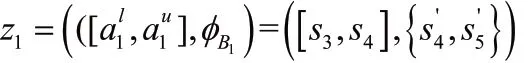
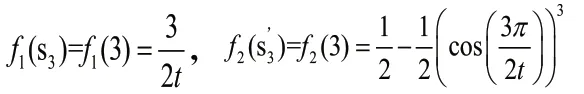
注：为合理精确地表示HULZNs,本文中LSF1是集合Az(x)的尺度函数，LSF2是集合Bz(x)的尺度函数。

语言尺度函数LSF1、LSF2满足以下3个性质：

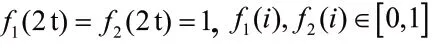
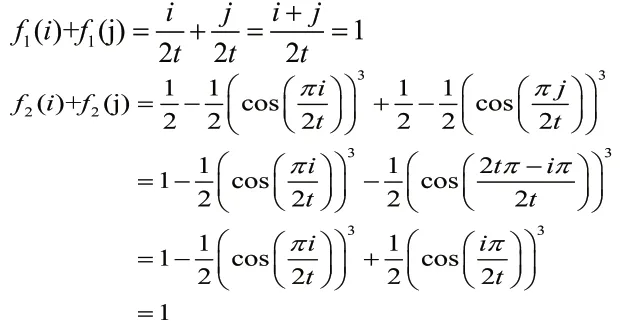
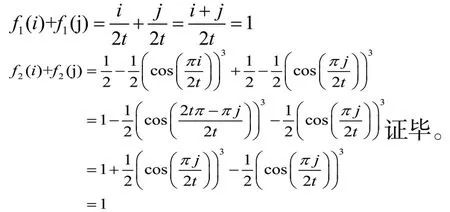
1.4 犹豫不确定语言型Z-Numbers

1.4.1 定义[12]Z-Number 是有序的模糊数对，记为。其中是对不确定变量X的限制，是对的可靠性的度量。

1.4.2 定义[12]设X是一个论域，

1.4.3 定义[12]设任意两个

1)加法算子

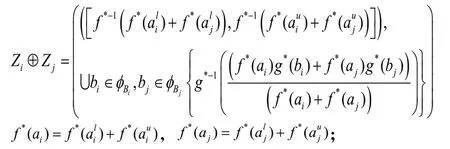
2)数乘算子

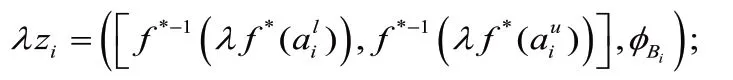
3)幂算子

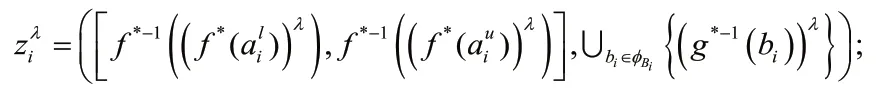
4)否定算子

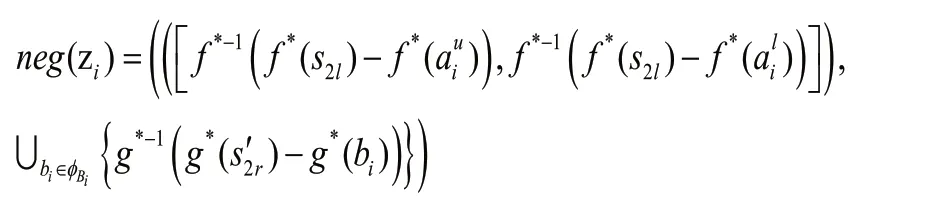
2 犹豫不确定语言型Z-numbers (HULZNs)的交叉熵与熵

在HULZN的模糊环境中度量两个模糊数之间的关系在实际应用中具有十分重要的作用。本文提出的HULZNs的相对交叉熵及熵，主要从其模糊性、犹豫性来度量两个HULZNs之间的不确定信息，并用于求权重以及相关的决策排序。

2.1 HULZNs的交叉熵

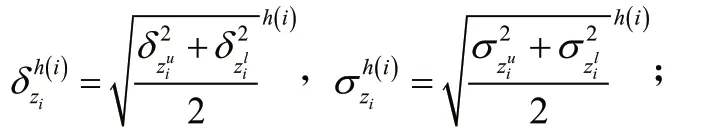
2.1.2 定义设任意两个犹豫不确定Z-numberzi，zi。相对于zj的相对交叉熵公式定义如下：

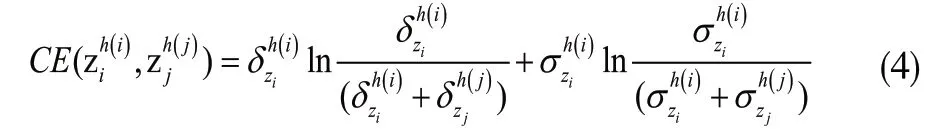
在讨论具体问题时，相对交叉熵公式不具备对称性。因此，定义相应完整的交叉熵公式。

2.1.3 定义设任意两个犹豫不确定Z-numberzi，zi；与zj的交叉熵公式定义如下：

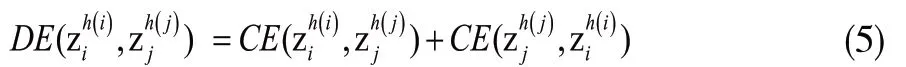
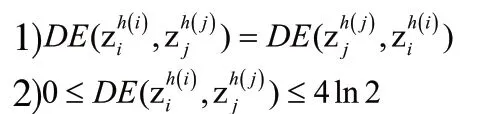
2.2 HULZNs的熵

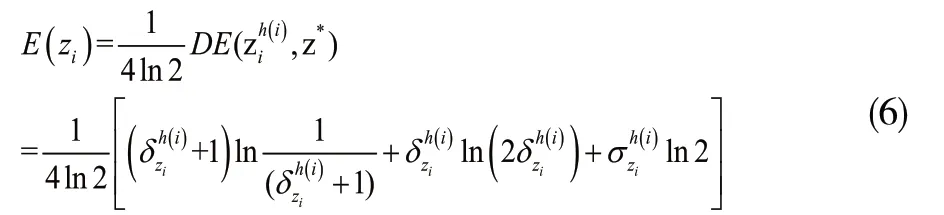
1)E(zi)=0当且仅当，zi是一个确定集，其中=0；

2)对任意的HULZNzi，；

证明：如果zi是一个确定集，即zi=z*，=1，=0得证毕。

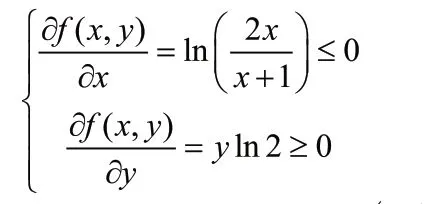
3 犹豫不确定语言型Z-numbers的多准则群决策方法

本节主要构造用于确定决策者权重和准则权重的优化模型，通过犹豫不确定语言型Z-numbers的交叉熵和熵来创建一种新型的多准则群决策方法。

犹豫不确定语言型Z-numbers的多准则群决策问题是由一组可供选择的方案构成。准则的权重满足；

3.1 构建最优模型确定权重

决策者权重和准则权重是未知待定或是部分未知的。由此，构建两个基于HULZNs熵度量的最优模型，用于计算决策者权重和准则权重。依据不同个体决策矩阵间的距离来计算决策者权重，决策个体权重越大表明其在决策过程中越重要。具体模型如下：

下面给出确定准则权重的最优模型：

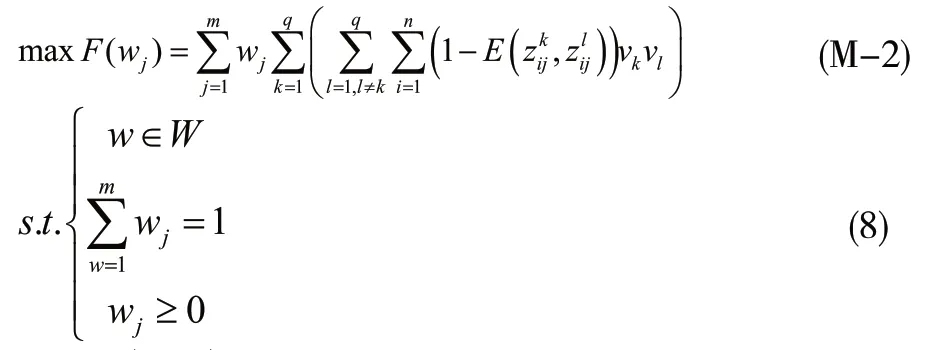
3.2 决策步骤

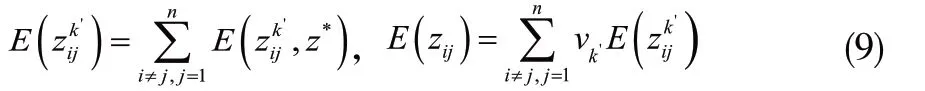
其中z*是一个确定集。

步骤5 计算各方案的拟合度得分并排序，得分最高即为最优方案

4 实例分析

某企业计划购进一种综合性能最优的企业资源规划系统，其选择标准分为四类：系统功能(c1)，供应商能力和信誉(c2)，系统合适度(c3)，系统灵活性(c4)。经3个专家的初步筛选，现有4个可供选择的企业资源规划系统。在激烈讨论后，给出关于决策者和标准的部分权重信息：

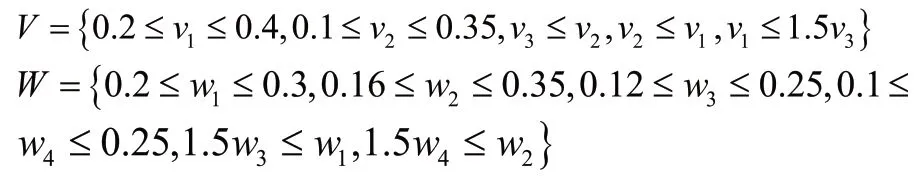
HULZNs的评估值见表1、2和3。

步骤2 根据公式(5)得到交叉熵矩阵：

表1 专家d1的性化推荐矩阵

表2 专家d2的性化推荐矩阵

表3 专家d3的性化推荐矩阵

步骤3 根据上文给出的最优化模型，得到决策者权重与标准权重分别是 ，

步骤4 结合求得的决策者权重和公式(6)，综合熵决策矩阵表示为：

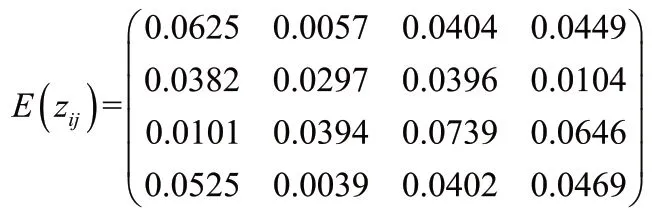
5 结论

本文给出了新的语言尺度函数及犹豫模糊不确定语言型Z-Numbers的熵，并提出基于语言尺度函数的距离公式，其简练且具有高分辨度，一定程度上解决了计算的复杂性和误差。 在最终的排序结果，本文得出的最优方案同文献[12]相同，但其他方案的排序略有不同。说明了本文决策步骤的可行性与有效性。