高速动车轴箱轴承疲劳寿命计算方法

李 震，商慧玲，张 旭，孙 伟

(1. 大连理工大学 机械工程学院， 辽宁 大连 116024；2. 北京金风科创风电设备有限公司 研发中心机械技术部, 北京 100176；3. 大连工业大学 机械工程及自动化学院， 辽宁 大连 116024)

轴承是高速动车的核心零部件之一，其承载动车总质量和各种复杂载荷，在保障高速动车稳定高速地运行过程中起着重要作用[1-2]。准确预测轴承的工作寿命极其必要, 预测值过大会埋下重大安全隐患，过于保守会导致材料物质浪费[3]。

国内外学者针对轴承的寿命问题做了大量研究。Jones等[4]基于轴承静力学模型研究了轴承的接触疲劳寿命；Ghaisas等[5]研究了轴承在固体润滑介质工作条件下的载荷特征与疲劳寿命，提出了针对角接触球轴承的动力学模型；Sakaguchi等[6]基于ADAMS动力学软件研究了实际工况下角接触球轴承的接触疲劳寿命；Bercea等[7-8]建立了轴承的拟静力学分析模型，研究了倾覆力矩与轴承游隙对其寿命特征的影响；万长森等[9]基于Lundberg和Palmgren轴承疲劳寿命方法，研究了角接触球轴承的寿命特征；杜冰等[10]基于弹性流体润滑理论开展了角接触球轴承寿命特征的研究工作；冷钢等[11]基于拟动力学分析软件得到轴承内部的载荷分布，同时考虑了过盈配合和温度等外在条件，研究了圆柱滚子轴承寿命的计算方法；吴子英等[12]针对铁路列车不同运行速度和不同可靠度条件建立三参数威布尔模型，研究了轴箱轴承的疲劳寿命。国内外对轴承寿命的研究主要集中于球轴承和圆柱滚子，对圆锥滚子轴承的寿命分析及其计算方法的研究则较少。

考虑上述问题，本文针对某型号高速动车，分析轴箱使用的双列圆锥滚子轴承，建立该类轴承的拟静力学模型，从而得到其内部载荷分布及疲劳寿命。比较了不同轴承疲劳寿命计算方法的差异，获得在不同工况下轴承的疲劳寿命特性，为高速动车轴箱轴承的研发设计及轴承疲劳寿命的准确预测提供了理论基础。

1 双列圆锥滚子轴承拟静力学模型

轴承拟静力学分析的基本思想是将高速运动轴承元件的离心力和陀螺力矩效应，与外载荷一起计入轴承的力和力矩平衡方程组，采用迭代方法求解这个非线性方程组[3]。

1.1 双列圆锥滚子轴承几何要素及载荷

双列圆锥滚子轴承在实际应用时有2种结构形式，即“面对面”和“背对背”结构。高速动车中的安装形式采用“背对背”结构，本文建立了包含(5+3n)个自由度的轴承拟静力学模型[13]，其中轴承内圈有5个自由度，每个轴承滚子有3个。该模型采用2个坐标系：固定在轴承外圈上的惯性坐标系oxyz，轴承中心为原点，见图1，其单位矢量为ex、ey、ez。F0为沿z轴方向的预紧力；Fz为轴向力；Fx、Fy分别为沿轴承半径方向的径向力；Mx、My分别为绕x、y轴的倾覆力矩。

另一个是固定在轴承滚子上的滚子坐标系owxwywzw，滚子大端中心为原点，见图2，其单位矢量为ewx、ewy、ewz。图2中,ρwe、ρwi、ρwf分别是滚子与外圈、内圈和挡边接触点的位置矢量；α、β、θ分别是外圈、内圈和挡边的接触角；γ是中间接触角；ε是滚子的半锥角。滚子坐标系相对于惯性坐标系的旋转矩阵MRN为

( 1 )

式中：ψ为滚子相对于惯性坐标系x轴的方位角。

拟静力学分析模型采用如下基本假设[14]：①轴承各部分结构的材料均为线弹性材料；②滚子轮廓和滚道轮廓均为直线；③忽略轴承内部的摩擦力和摩擦力矩；④忽略轴承保持架的影响；⑤轴承的外圈固定。双列圆锥滚子轴承工作时，承受如下载荷(见图1)：F0(为了保证负游隙Ga)，Fz、Fx、Fy，Mx、My。

滚子和内圈在外部载荷作用下会产生旋转和平移运动，使得偏离其初始位置。在惯性坐标系中采用平移向量U和旋转向量Φ为轴承内圈的位移

U=[ux,uy,uz]T

( 2 )

Φ=[φx,φy,0]T

( 3 )

式中：ux,、uy、uz、φx、φy分别为轴承内圈相对于惯性坐标系的线位移及角位移。

为描述轴承滚子在平衡时的位移，在滚子坐标系中采用平移向量Um及旋转向量Φm表示

Um=[0,umy,umz]T

( 4 )

Φm=[φmx,0,0]T

( 5 )

式中：umy、umz、φmx分别为轴承滚子在滚子坐标系下的线位移与角位移；m为滚子所在位置，m=1为左侧滚子，m=2为右侧滚子。

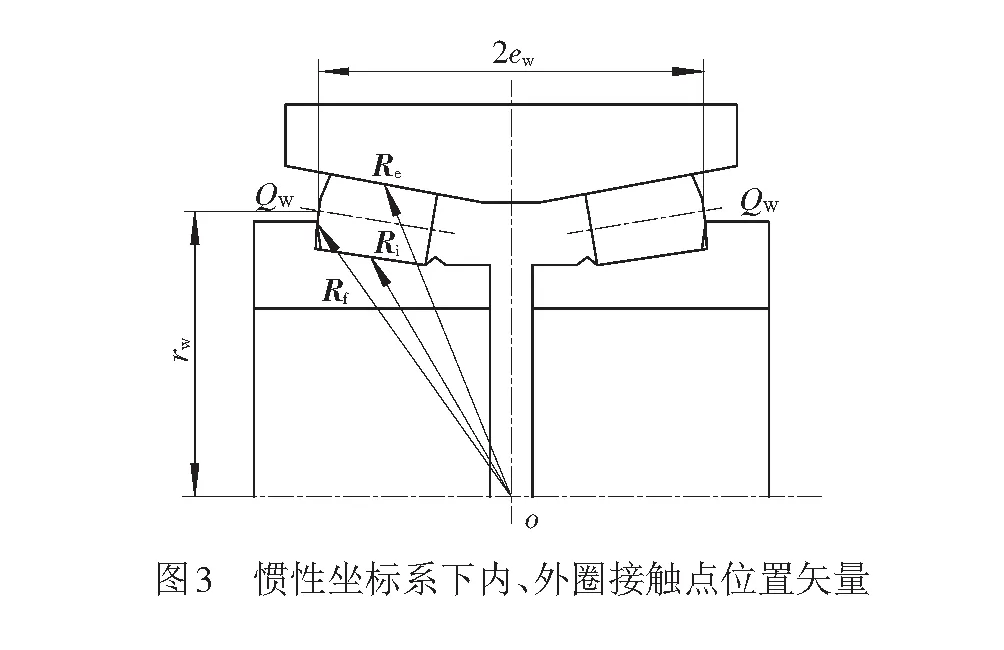
1.2 圆锥滚子的受力特征及轴承平衡方程1.2.1 内圈接触点位置矢量

惯性坐标系下内、外圈接触点位置矢量见图3。图3中，ew和rw分别是轴承初始状态下滚子坐标系原点到惯性坐标系y和z轴的距离，Re、Ri、Rf分别是外圈、内圈和挡边与滚子的接触点矢量，其表达式为

( 6 )

施加载荷后，内圈的平移矢量为

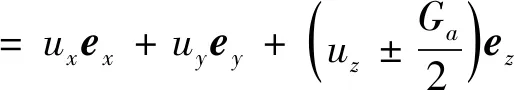
( 7 )

式中：“+”为左侧内圈，“-”为右侧内圈。

角位移φx、φy生成的旋转矩阵MI为

( 8 )

( 9 )

1.2.2 滚子触点位置矢量

轴承滚子变形之前，滚子与外圈、内圈和挡边接触点的位置矢量(图2)在滚子坐标系中表示为

(10)

施加载荷后，滚子的平移矢量为

Λ=μmyewy+μmzewz

(11)

角位移φmx生成的旋转矩阵MR为

(12)

因此，滚子变形后，其与外圈、内圈和挡边接触点的位置矢量为

(13)

1.2.3 各接触点位置法线方向的形变和受力

如图3所示，滚子坐标系原点ow的位置矢量为

Uw=rmcosψex+rmsinψey∓ewez

(14)

式中:“-”为左侧滚子；“+”为右侧滚子。

内圈、外圈和挡边接触位置的单位法向量为

(15)

施加载荷后，轴承在外圈、内圈和挡边各个接触位置发生的形变可表示为

(16)

基于赫兹接触理论，滚子与轴承内外圈的变形与接触载荷关系的经验公式为

(17)

式中：Q为滚子载荷；l为滚子长度。

滚子与档边是点接触形式，其接触载荷和变形的关系为[15]

(18)

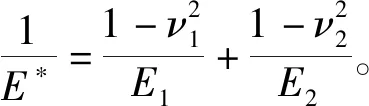
1.2.4 轴承平衡方程

滚子受力图见图4，其中，Qe、Qi和Qf分别为给定位移条件下轴承滚子与外圈、内圈和挡边接触处的载荷；Fc为滚子的离心力；Tc为离心力形成的力矩；Tg为轴承滚子的陀螺力矩。滚子的离心力Fc为

(19)

式中：ρ为轴承滚动体的密度；V为轴承滚动体的体积；nm为轴承滚动体绕轴承轴线转动时的速度；rg为轴承滚子重心相对应圆的半径。

轴承滚子的陀螺力矩Tg为

(20)

式中：J为惯性矩；ωm为轴承滚动体绕轴承轴线转动时的角速度；ωr为轴承滚动体绕自身轴线旋转时的角速度。

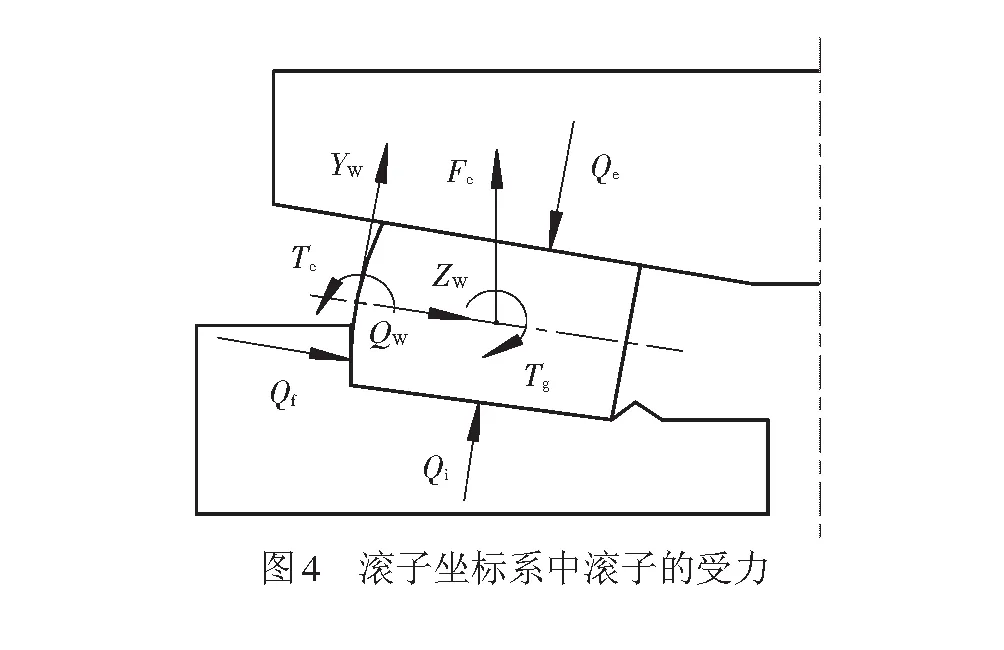
如图4所示，在滚子坐标系中滚子平衡方程可以表示为

(21)

式中：Te、Ti和Tf分别是外圈、内圈和挡边接触载荷在滚子坐标系中的力矩。

轴承的整体平衡方程在惯性坐标系表示为

(22)

式中：Qex、Qey、Qex分别为Qe在惯性坐标系中的分量；Tex、Tey分别为Qe惯性坐标系中形成的力矩分量；Z为单列滚子数。

1.3 轴承拟静力学模型的求解

轴承拟静力学计算流程见图5。

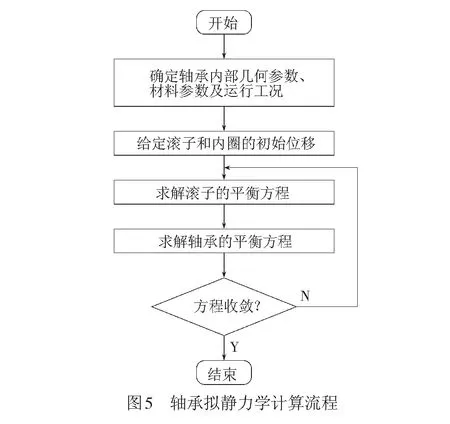
为了快速求解拟静力学平衡方程，基于符号运算工具包(SymPy) ，推导并化简了轴承载荷计算公式，具体程序代码可参考网址进行查看[16]。在此基础上，利用数值分析工具包(NumPy, SciPy)求解该非线性平衡方程组，计算过程见图5。在轴承结构和工况确定之后，设定轴承滚子及轴承内圈的初始位移，然后对滚子和轴承的力学平衡方程组进行迭代求解，直至获得最终的收敛解。利用迭代计算求得的位移解，可以计算轴承内部的各种载荷，并将其应用于后续轴承寿命的计算。

2 轴承的疲劳寿命

当前主要有3种方法用于计算滚动轴承的额定寿命。方法一是基于ISO 281—2007标准的计算方法；方法二是基于次表层应力的Lundberg和Palmgren理论计算方法；方法三是改进的L-P理论计算方法。

2.1 ISO标准中滚子轴承的基本额定寿命计算

轴承疲劳寿命计算采用如下假设：①支撑轴承的套圈具有刚性特征；②轴承具有较低转速时不考虑离心力及陀螺力矩；③轴承的内部游隙在轴承承受径向载荷时认为是零；④针对名义接触角，角接触轴承被认为是常数；⑤对于滚子轴承，滚子和轴承滚道之间相互接触，其间载荷认为是分布均匀的[17]。

依据ISO281—2007[18]，针对径向滚子轴承，其基本额定动载荷为

(23)

式中：bm为经常使用的淬硬轴承钢与良好的制造方法的额定系数[19]；fc为与轴承零部件的形状、精度和材料特征相关的系数，其值由Dwecosα/Dpw查表确定；Dwe为轴承滚子的直径，针对圆锥滚子而言，其值为滚子的大端与小端直径和的一半；α为滚子轴承结构中的公称接触角；Dpw为轴承滚子结构的节圆直径；i为轴承滚子的列数；Lwe为轴承滚子的实际有效作用长度；Z为轴承滚子的个数。

当轴承在保持定值的轴向载荷、径向载荷的共同作用下，轴承的径向当量动载荷为

Pr=XFr+YFa

(24)

针对基本的额定寿命，轴承的寿命[20]为

(25)

式中：L10为基本额定寿命，百万转。

2.2 L-P理论滚子轴承基本额定寿命计算

对于滚子轴承的滚道，额定的动载荷为

(26)

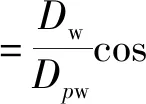
相对于承受的外部载荷来说，轴承的内圈是在做旋转运动，内圈的当量载荷为

(27)

因此，轴承的内圈寿命为

(28)

外圈相对于轴承外部载荷处于静止状态，则外圈的当量载荷为

(29)

因此，轴承外圈的寿命为

(30)

综上，计算的轴承的基本额定寿命为

(31)

修正之后的轴承额定寿命为

(32)

式中：修正系数bm可以基于轴承的类型进行考虑。

双列圆锥滚子轴承的寿命计算为

(33)

式中：Lnm1、Lnm2分别为左侧轴承、右侧轴承修正之后的额定寿命。

上述轴承寿命计算方法过于严格，为简化计算过程，针对刚性套圈中等转速的滚子轴承Lundberg 和Palmgren提出了如下近似公式[20]

Qei=QmaxJ1

(34)

(35)

Qeo=QmaxJ2

(36)

(37)

2.3 改进的L-P方法中轴承的额定寿命

当轴承承受复合载荷时，即同时受到径向力和弯矩等作用，导致轴承的内部载荷实际分布特征与标准中规定的分布特征出现偏差，同时也使得沿滚子长度方向的载荷产生偏载等。而L-P寿命公式未考虑以上偏差与偏载等对轴承寿命的影响。

Harris考虑轴承承受复合载荷时，轴承的内部载荷实际分布特征和周向的应力对轴承寿命的影响，根据轴承的额定动载荷方法，进一步将L-P方法做了深入研究。沿着轴承滚子的长度方向，把有效接触长度值l的轴承滚道，划分成T个小段[3]。考虑轴承滚道的切片，其疲劳寿命如下

(38)

式中：QC,k,m,t为轴承滚动体-滚道切片的基本额定动载荷；QE,k,m,t为位于同列的轴承滚道上面的当量接触载荷值；t为切成的第t个片段；m=1为左侧轴承，m=2为右侧轴承。

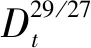
(39)

式中：Dt为第t个切成片段的直径；dpt为第t个切片轴承的节圆直径。

针对转动轴承内滚道

(40)

针对固定的轴承外滚道

(41)

滚道结构整体的寿命为

(42)

滚子-滚道相接触的时候，考虑滚子薄片，其基本的额定动载荷(单位为106转)为

qC,j,k,t=464(1∓γ*)1.324(Δl)7/9Dt29/27

(43)

当轴承滚子与内外滚道相接触，滚子薄片和滚道薄片的寿命计算方法相一致，轴承滚动体—内外圈滚道切片的疲劳寿命为

(44)

把轴承滚子的转动数转换成套圈的转动数，当内圈转动一周时，轴承滚子的转动数N为

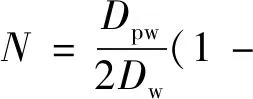
(45)

综合滚子的寿命和内外滚道的寿命，双列圆锥滚子轴承的整体寿命为[3]

(46)

3 高速动车轴箱轴承分析

某高速动车的轴箱轴承实际工作条件为：动车的单根轴重为17 t,通过计算得到轴承承受的径向载荷值约等于95 kN，轴向载荷值约等于25 kN(该值根据轴载荷的15%计算得到)。双列圆锥滚子轴承结构参数见表1。

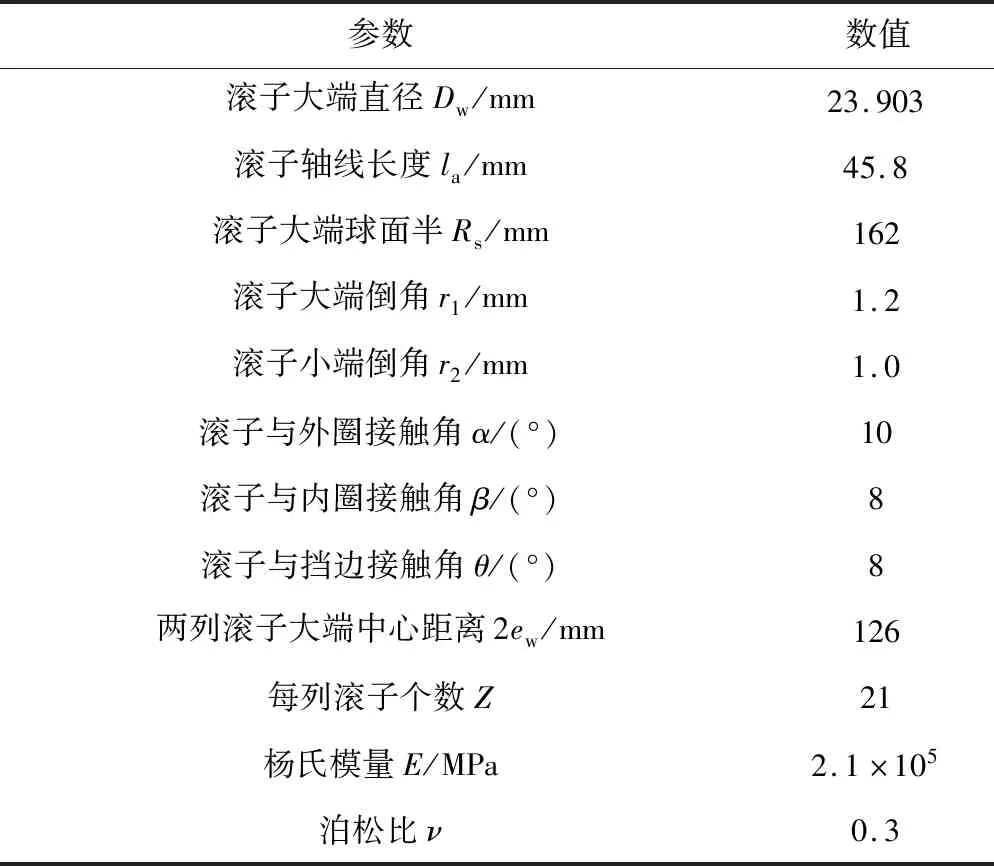
表1 双列圆锥滚子轴承结构参数[14]

3.1 轴承内部的载荷特征

滚子与内圈滚道、挡边接触载荷特征见图6。

图6的工况条件为：Fy=90 kN，Fz=25 kN，高速动车运行速度为250 km/h，轴承存在的负游隙值Ga，分别为0.10、0.15、0.20 mm。当轴承承受着相同的外部施加载荷时，轴承内部承受的接触载荷值，随着轴承自身负游隙值的增大而增大，导致轴承的额定承载值更加容易达到。同时，当轴承负游隙值增大时，处于轴承内部不同位置的滚子，与内圈挡边及滚道的接触载荷值的大小差异也变的越来越小，使得在轴承内部的各滚子承受的载荷分布更加均匀。

在列车不同速度下，第一列滚子与内圈滚道、挡边接触载荷特征，见图7—图9。单个滚子所受的离心力及滚子附加力矩和陀螺力矩。

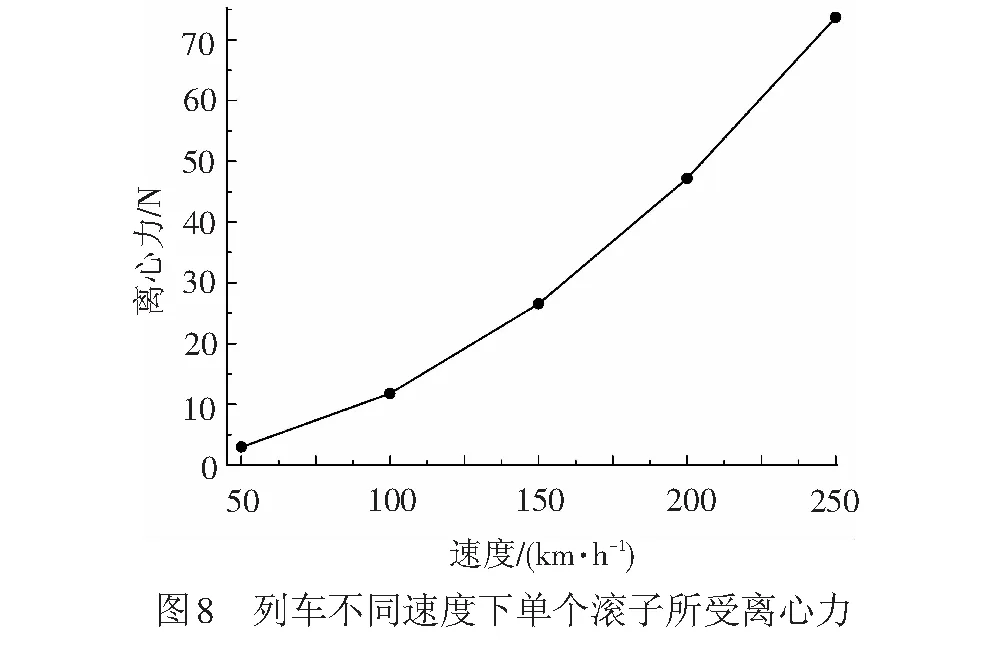
图7工况条件为：Fy=90 kN，Fz=25 kN，轴承负游隙值Ga=0.10 mm。在高速列车速度从50 km/h增加到250 km/h过程中，轴承滚子和内圈滚道在接触时的最大载荷值仅仅增大了36.8 N, 轴承滚子和内圈挡边在接触时的最大载荷值仅仅增大了11.01 N。由图8、图9中可以发现，轴承滚子的离心力最大值为74 N，附加力矩的最大值为1.63 N·m。其与外载荷相比较，高速列车速度变化产生的离心效应，对轴承内部各滚子载荷特征的影响并不明显，因此对于该动车轴箱轴承，采用静力学模型即可达到分析要求。

3.2 ISO标准计算方法与L-P理论计算方法的对比分析

轴承寿命随径向、轴向载荷变化2种算法对比见图10。

由图10可见，当轴承的径向与轴向载荷增大时，计算出的轴承寿命均在逐渐变小。当轴承载荷条件相同时，L-P理论计算较ISO标准算法得出的寿命值要小许多。原因之一是ISO标准算法中，没有考虑到陀螺力矩和离心力的存在对轴承寿命的影响；其二是当给轴承施加轴向预载荷时，轴承的径向游隙值会产生增大效应，增大的游隙值使得轴承内部各滚子的载荷分布情况发生较大变化，而ISO标准的计算算法中却将轴承游隙值假定为零。由图10还可以发现，基于以上2种计算方法所获得的轴承寿命预测结果的差值，随负游隙值的减小而变的越来越小，随载荷的减小而变的越来越大。

3.3 L-P理论计算方法与改进的L-P理论计算方法对比分析

轴承寿命随径向、轴向荷载变化中，L-P方法与改进L-P方法对比见图11。

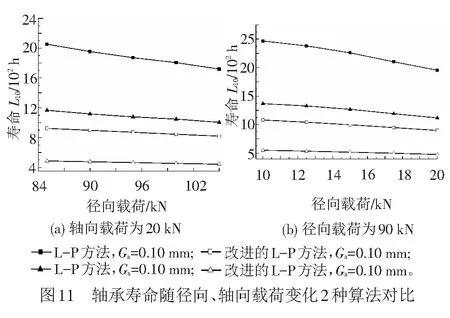
由图11可以看到，2种计算方法中，轴承寿命均随轴承承受的径向与轴向载荷值的变大而逐渐减小。改进的L-P方法比L-P方法计算得到的轴承寿命结果要小，是因为其在计算过程中将滚动体的寿命作了考虑。改进的L-P方法分析得到的轴承寿命结果大约是L-P理论计算结果的45%，并且这个比值不会随着轴承载荷大小和游隙值的变化而改变，其原因是这2种计算方法采用的都是轴承内部的载荷特征，当游隙变化导致载荷分布发生变化时，对2种方法产生的影响是相同的。

通过以上分析可知，采用不同的方法计算轴承疲劳寿命，结果差异较大。轴承在真实的工作环境中，往往承受着复合载荷，如径向载荷与弯矩等，这要求实际研究时建立合适的轴承力学模型，同时采用改进的L-P理论去计算轴承的疲劳寿命特征，能够更全面、准确地预测轴承实际工作时的疲劳寿命。

4 结论

(1) 本研究建立了包含(5+3n)个自由度的高速动车双列圆锥滚子轴承的拟静力学模型，获得了轴承在不同游隙值与不同运行速度下的内部载荷分布情况。轴承的内部载荷值随着轴承负游隙值的增大而增大；当列车运行速度发生变化时，轴承内部的载荷分布情况变化不大。

(2) 比较ISO标准方法与L-P理论方法的计算结果，前者因未考虑轴承的离心效应与游隙等因素，使得利用ISO标准方法计算出的轴承寿命比利用L-P理论计算的轴承寿命值要大；同时，2种计算方法所得寿命结果的差异随着轴承游隙值的减小而逐渐减小。

(3) 比较L-P理论方法与改进的L-P理论方法的计算结果，后者在计算过程中考虑了滚动体带来的影响，使得计算得到的轴承寿命值最小；同时，当轴承的游隙值发生变化时，2种计算方法计算结果的比值并不会随着改变。