解泊松问题的Peaceman-Rachford迭代法，共轭梯度和预处理共轭梯度法

张颖颖

(中国传媒大学信息科学与技术学部，北京 100024)

1 引言

假设：上述边值问题有唯一解，且连续依赖于边界条件和右端项，亦即边值问题是适定的。[1]

2 背景

在用数值方法解possion方程时，根据方程的特点，选择了三种适合求解大型方程组的求解器来解方程。

这三种方法为Peaceman-Rachford迭代法，共轭梯度法和预处理共轭梯度法，并对这三种方法的求解效率进行比较。

3 Possion方程边值问题求解实例

例2.设对Possion方程边值问题

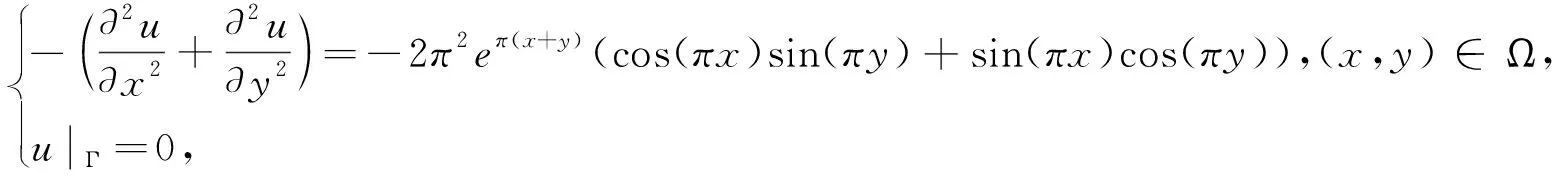
3.1 Peaceman-Rachford迭代格式

采用正方形网格剖分正方形区域Ω(步长为h)，对x和y方向采用中心差分并记

则对Possion方程离散后差分格式可写成：L1uh+L2uh=f。

改写为uh=uh-τ(L1uh+L2uh-f)，

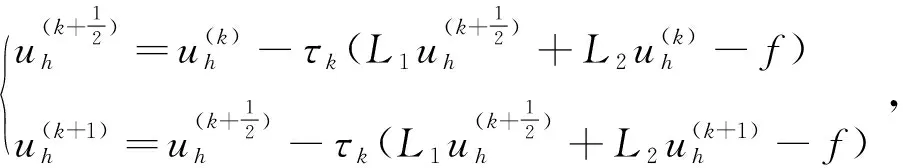
其分量形式为

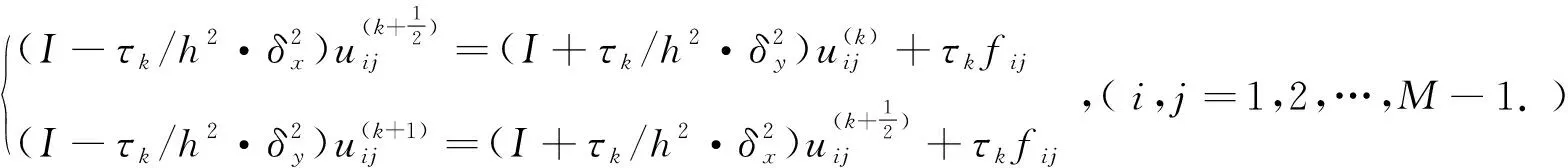
3.2 共轭梯度法(CG)

设A表示N阶对称正定阵，考虑线性方程组

Au=f，

(1)

其中u为未知向量，f为已知向量.以p(k)表示第k步的搜索方向，u(k)表示第k步近似解向量，残向量r(k)=f-Au(k)，则用共轭梯度法求解(1)的步骤如下：

(1)取初始近似值u(0)，计算p(0)=r(0)=f-Au(0)

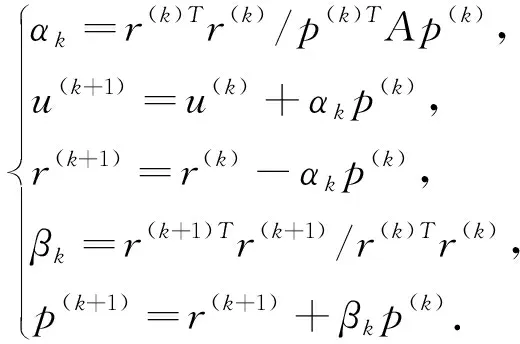
3.3 预处理共轭梯度法(PCG)

设A表示N阶对称正定阵，考虑线性方程组

Au=f，

(1)

其中u为未知向量，f为已知向量.以p(k)表示第k步的搜索方向，u(k)表示第k步近似解向量，残向量r(k)=f-Au(k)，则用预处理共轭梯度法求解的步骤如下：

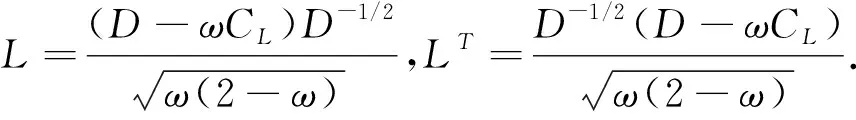
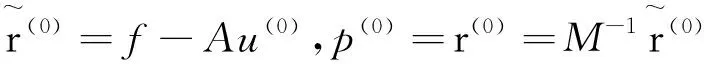
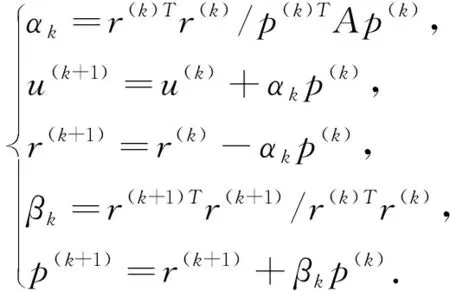
4 实例的三种方法比较

利用Matlab运行二种数值解法的语言程序，[5]求解本文中的实例，求解区间[0，1]，取不同步长h，得到不同数据结果和图形。为进一步分析结果绘制如图表格。

例1 取步长h=0.1时 所得的图形如下

图1.1 图1.2

图1.3 图1.4 真解图形

表1 数值结果

从表1可以看出CG方法迭代次数最少，此法较为优越。

例2 取步长h=0.05时 所得的图形如下

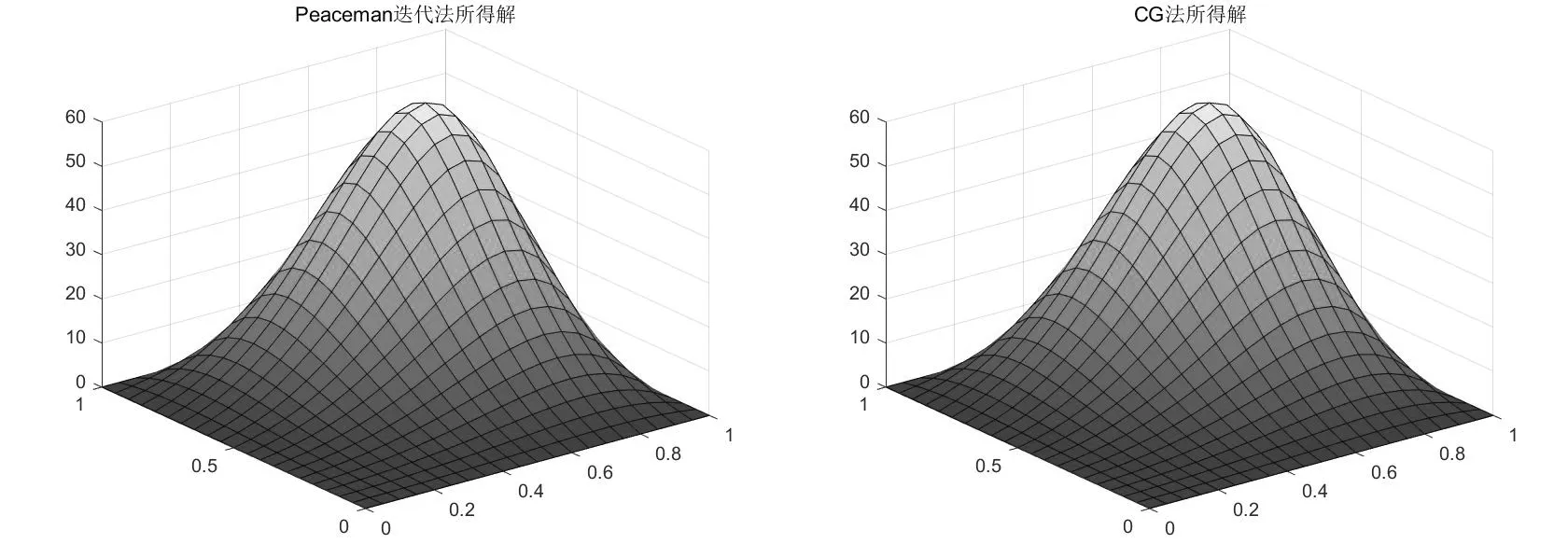
图2.1 图2.2

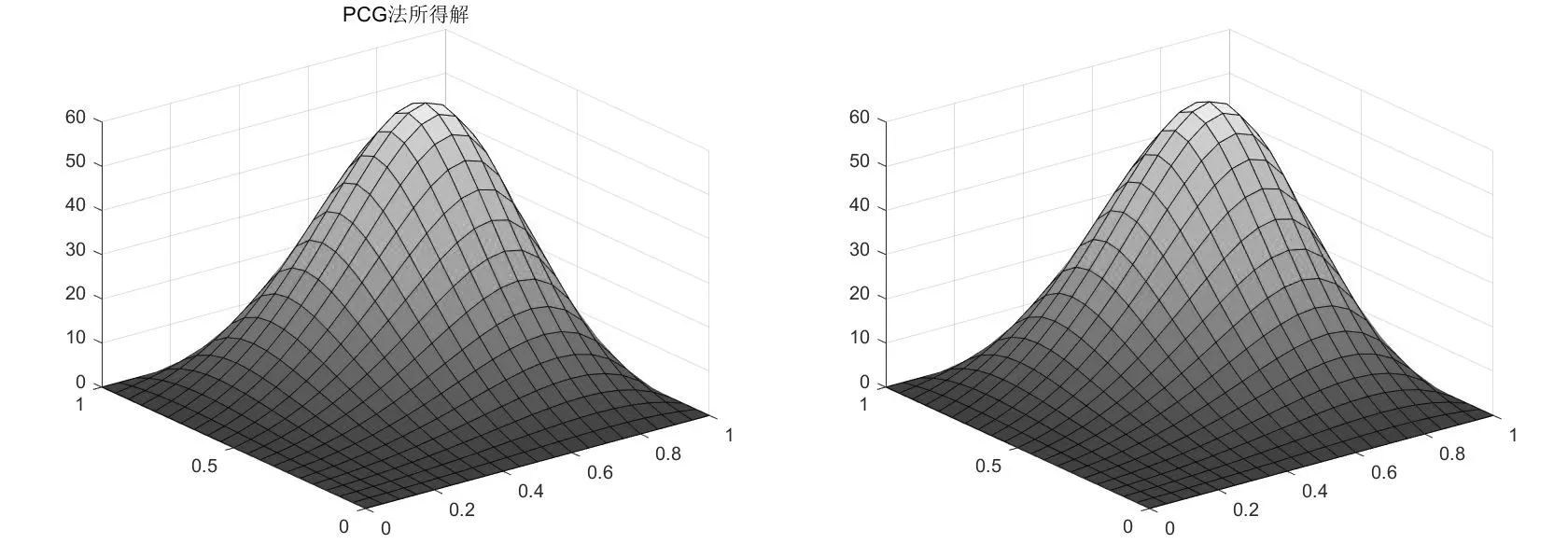
图2.3 图2.4 真解图形

表2 数值结果

从表2数据可以得出PCG方法迭代次数最少，此法较为优越。

5 结论

针对同一问题，步长h越大，迭代次数越多，但是误差越小，结果越精确。

这三种方法中，共轭梯度法不稳定，如果条件符合共轭梯度法使用的条件，那么收敛很快，但是如果条件不符合，收敛会很慢，迭代次数会很多。

Peaceman-Rachford迭代法和预处理共轭梯度法都比较稳定，而且在两个例子中预处理共轭梯度法的迭代次数都比Peaceman-Rachford迭代法的迭代次数少。综上，三种方法中最好的解决Possion方程问题的方法是预处理共轭梯度法。