操作·联想·迁移

钱德春

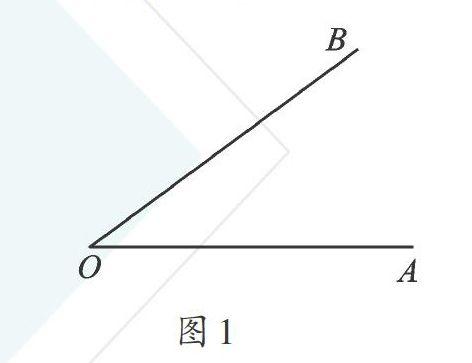
在本章中，有一个用直尺和圆规“作一个角等于已知角”的问题。我们原来没有接触过尺规作图，同学们在作图时可能会根据教材上的作法（如图1的作法）依葫芦画瓢，没有认真思考“这种作法是怎么想到的？”“这样作图正确吗？”，以致过几天老师再让大家画图时，大家依然无所适从。

作法：

1.以点O为圆心，任意长为半径，用圆规画弧，分别交OA、OB于点C、D。

2.任意画一点O′，画射线O′A′。以点O′为圆心，OC长为半径画弧，交O′A′于点C′。

3.以點C为圆心，CD长为半径画弧，交前弧于点，D′。

4.过点D′画射线O′B′。∠A′O′B′就是与ZAOB相等的角。

接下来，钱老师来帮你解决这个困惑。

这里，我们重点谈一谈“这种作法是怎么想到的”。请同学们跟着下面内容，一边操作，一边思考，并回答问题。相信通过你的操作、思考与回答，问题就能解决了。

活动一：

1.操作。

已知∠AOB，用量角器画∠A′O′B′，使∠A′O′B′=∠AOB。

2.思考与问答。

（1）你是怎么画图的？

答：用量角器先量出已知角的度数，再画一个等于所量得度数的角。

（2）你是如何用量角器先量出已知角的度数的？

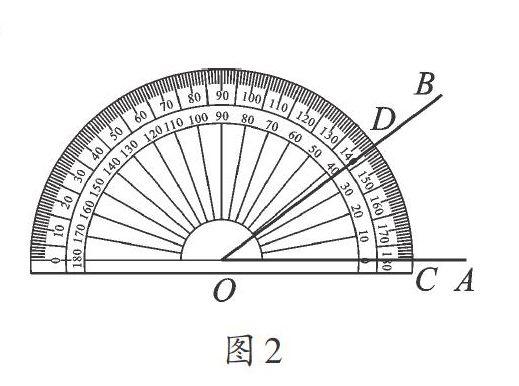
答：如图2，将量角器的中心与∠AOB的顶点O重合，零刻度线与ZAOB的边OA重合，读出另一边OB对应的读数。

（3）要作∠A′O′B′等于∠AOB，你觉得画图的关键是什么？

答：确定点D的具体位置。

（4）如果这个量角器上没有刻度，你怎么办？

答：在量角器上做出点D位置的记号。

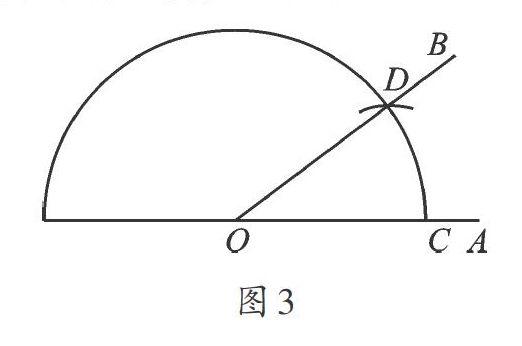
（5）此时量角器只能起到什么作用？

答：圆弧的作用（如图3）。

（6）如果连这个没有刻度的量角器都没有，你能不能找到什么工具代替它呢？

答：圆规。

到这里，同学们有没有对尺规作图的方法豁然开朗呢？

活动二：

1.操作。

已知ZAOB，用直尺和圆规作∠A′O′B′，使∠A′O′B′=∠AOB。

2.思考与问答。

（1）说出作图步骤（作出的图如图4，作图步骤见图1的作法）。

（2）这样作出的∠A′O′B′一定与∠AOB相等吗？（有兴趣的同学可以思考一下哦！到了八年级大家就知道了。）

同学们，用直尺和圆规“作一个角等于已知角”的方法是由量角器进行联想和迁移而来。有时，我们在遇到一些问题时，不妨就近联想。通过借鉴、迁移、联想的方法，你或许会打开新的思路。