美国人口的预测

刘亚平 刘云忠

摘 要：考虑到人口连续变化的规律，用微分方程解出人口数随时间变化的规律，求得人口净增长率，并对美国1980年以后的人口数进行计算，发现与实际数据不符，继而对原来模型进行改进。利用1790—1850年、1860—1920年、1930—2000年这三个时间段的数据建立指数增长模型，对未来美国总人口进行预测，发现在短时间内，美国人口随着时间的推移而不断增长。

关键词：美国;人口预测;马尔萨斯人口增长模型;指数增长模型

中图分类号：C923        文献标志码：A      文章编号：1673-291X（2020）03-0175-03

一、人口预测方法

人口问题是当前人们最关心的问题之一，对未来人口进行预测，有效控制人口增长，首先要正确认识人口变化的规律。本文通过对美国1790—1850年、1860—1920年、1930—2000年这三个时间段分别建立指数增长模型，确定三个时间段的人口增长率，并对三个模型进行检验。利用1790—1980年间美国每隔10年的人口数据建立马尔萨斯人口增长模型，并对每隔10年的人口数量进行预测，然后与实际数据进行对比。如果二者差异较大，则改进以上模型，寻找更加合适的模型来进行预测和分析。

二、基本假设

假设1：人口数量的变化不受外界大环境的影响。

假设2：各年的人口数据真实准确。

假设3：人口增长率记为r，记时刻t的人口为x（t），初始时刻t=0时人口数为x0。

假设4：马尔萨斯人口模型中，一是记单位时间人口增长率为常数r，二是t时刻人口x（t）对t连续可微。

假设5：指数增长模型中，假设人口净增长率为变量r。

三、建立模型

（一）建立马尔萨斯人口增长模型

记1790年美国人口数为x1790，在t至t+？驻t这一时间内，美国人口的增量为：

（二）求解马尔萨斯模型

根据实际数据，利用线性最小二乘法直接进行参数估计比较麻烦，因此在两边取对数，记lnx（t）=y，lnx1790=ln3.9=1.36=a，则原方程化为y=a+r（t-1790）。利用1790—1900年的数据进行拟合，得到r=0.02142。

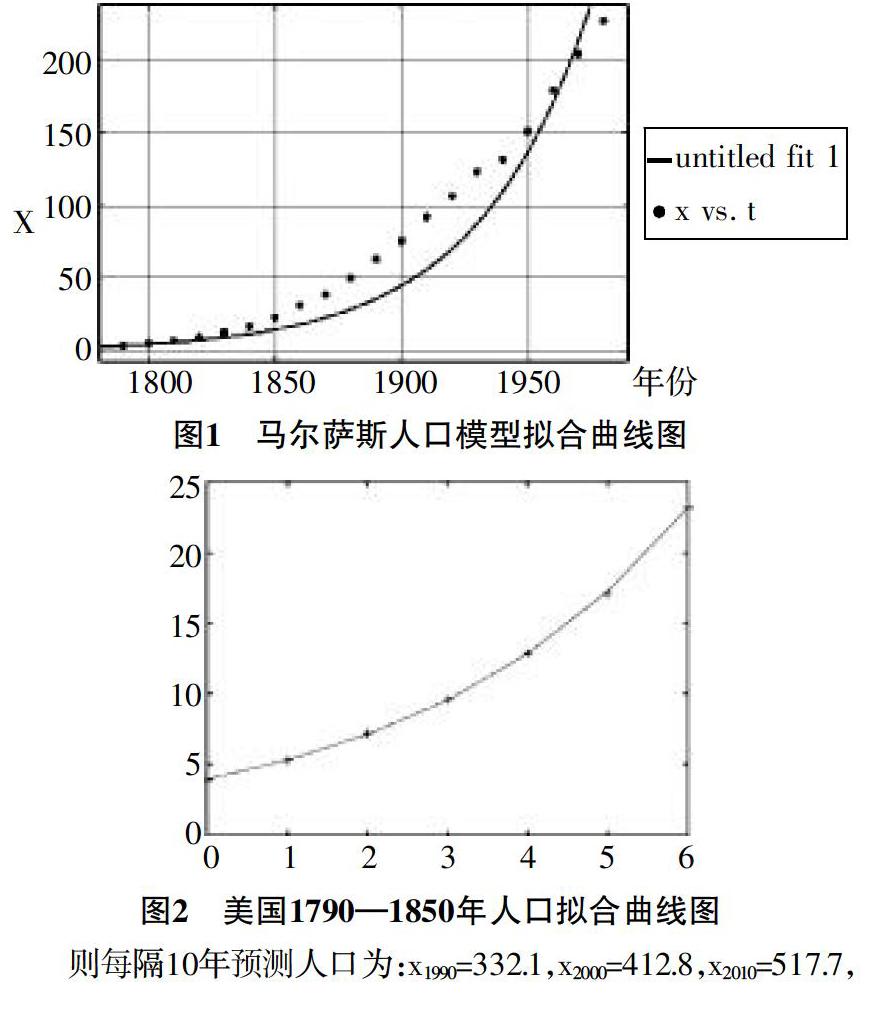
另外，利用Matlab可以得到预测数据与實际数据的对比结果（如图1所示），其中实线表示利用马尔萨斯人口模型预测的美国人口数据，正方形黑点表示美国实际的人口数据。

则每隔10年预测人口为：x1990=332.1，x2000=412.8，x2010=517.7，x2020=646.5，x2030=799.3。然而查阅美国相关年份人口数据，美国1990年的实际人口为248.7百万，2000年的实际人口为281.4百万，2010年的实际人口为307.0百万。通过这三个数据就可以发现，利用马尔萨斯模型预测的人口数与实际人口数出入较大，因此改进马尔萨斯人口增长模型，以得到更加符合实际情况的人口增长模型。

（三）建立指数增长模型

事实上，人口增长率受实际生活中诸多因素的制约，不可能是一成不变的。因此，假设人口增长率线性递减。在排除一切外界干扰因素的影响下，根据实际数据，建立指数增长模型，其中记当年人口数为x0，10年以后的人口数为x1，增长率为r保持不变，则：

（四）对指数增长模型求解

利用Matlab和模型（1）对1790—2000年的数据进行拟合，现对问题进行变形处理，对x（t）=x0ert两边取对数可得lnx（t）=lnx0+rt。用Matlab可得到：r1=0.2956，x0=3.9401。

所以，1790—1850年的拟合函数为线性函数lnx（t）=1.3712+0.2956t，即x（t）=3.9401e0.2956t，由Matlab得到拟合函数，与离散图的图像进行对比，得到本文图2。

比较拟合的曲线图与散点图可以发现，与实际人口数据的增长情况相吻合（见图2）。

类似的，可以发现，1860—1920年、1930—2000年与实际人口数据的增长情况相吻合（见图3、图4），对应的拟合函数分别为：

（五）模型评价

根据三个模型，分别求出用指数增长模型预测的1800—1850年、1860—1920年、1930—2000年的人口数（见本文表1至表3）。

由此可见，相对于马尔萨斯人口模型，在短期内运用指数增长模型对人口数进行预测是比较准确的。但该模型中，人口数将随着时间的增长而无限增长，显然，这与实际情况不符。在资源与环境等因素的干扰下，人口是不可能无限增长的，当增长到一定的程度后，增长速率将会慢下来。因此，为了更好地预测人口的增长趋势，需要研究更贴近实际的模型来解决此类问题。

参考文献：

[1]  杨颖.数学建模在实践中的应用[J].长春师范学院学报，2010，（12）：106-108.

[2]  张健.将数学建模思想融入数值分析课堂的探讨[J].中国电力教育，2012，（17）：70-71.

[3]  刘令，杨力，林源.基于指数增长模型的全国人口预测[J].山东工业技术，2014，（16）：164.