乏燃料多式联运动态风险评估研究
张洋,李荷华
(1.上海第二工业大学 经济与管理学院,上海 201206;2.上海第二工业大学 管理科学与工程学院,上海 201206)
0 引言
核电站乏燃料,是指核电站反应堆中定期被替换出来的能量已释放到不能满足发电需要的核燃料[1]。乏燃料作为一种危险货物在运输时,当其运输容器受损会对周边人员、环境造成较高的伤害和损坏。而根据我国核电机组的运行情况,到2020年,核电站卸出的乏燃料累积量将达到9 000 tHM左右[2]。我国核发电站主要位于东部沿海,乏燃料后处理厂多处于西北腹地,其间运输距离长达4 000 km,需跨越多个省(市、自治区)[3],其运输面临着量大、长距离以及安全的问题。乏燃料作为高放射性物质,在其运输过程中应该控制其发生危险的可能性,降低运输风险。
由于实际运输过程中不断变化的内部和外部因素条件,采用动态的方法评估量化风险更加切合实际。近年来,国内外专家通过考虑系统内部和外部条件的动态演变,影响风险评估。如基于事件序列图(ESD)的动态风险建模[4],通过贝叶斯推理和似然函数来更新风险概率[5],基于贝叶斯理论更新后故障密度函数的动态FMEA方法[6],后续转换函数和仿真模拟的动态风险评估概念模型[7]。以上方法都是对内部和外部风险数据的仿真推理来动态更新概率,没有考虑到风险间传递的因素。
据2007年统计,1.11×109t危险货物通过美国多式联运系统运输[8],而我国早在1991~1992年讨论的大亚湾核电站乏燃料运输问题就采用“固定一个中转港和一条铁路专线”的水陆联运为最佳方案[9-10]。所以,乏燃料采用多式联运是切实可行的,也是未来的趋势。
笔者基于动态延迟的风险评估方法,根据乏燃料特征和实际状况对该方法进行了改进,使其更符合乏燃料运输的动态风险评估需要。在对乏燃料的多式联运过程进行风险评估时,将风险的变化,通过运输延迟的概率,动态演变表现出来,然后通过故障树分析运输途中会发生的乏燃料泄漏风险,从而作为导致延迟的主要风险,并结合故障树,通过改进的熵权层次分析法确定各风险的权重,最终根据乏燃料特性评估风险。
1 动态风险评估模型
以往研究通过对200起危险化学品事故进行分析,总结了在运输过程中风险发生的环节,并从“在行驶时发生事故”和“非行驶时发生事故”两方面进行风险划分[11]。笔者根据前人研究,结合乏燃料运输自身特性,进行了故障树分析,具体结果如图1所示。
考虑到乏燃料运输的特殊性,本文通过分析选择四种多式联运过程中影响后果最大的风险进行研究,分别是交通相撞风险、环境因素事故风险、车辆及设备损坏风险、装卸搬运损坏风险。然后评估出风险发生概率和后果。
1.1 风险权重的确定
本文研究的四种风险分别位于故障树的不同层级,为了使得到的权重更加符合实际情况,采用改进的熵权层次分析法确定权重[12]。根据本文研究背景,具体步骤如下:
① 通过层次分析法判断矩阵求得上层风险权重值β=(β1,β2,…,βm),各底层风险权重Ф=(Ф1,Ф2,…,Фn)。
② 设熵权法得到的各风险因素权重ω0=(α1,α2,…,αn)。
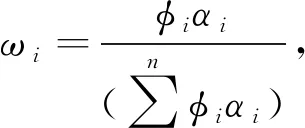
④ 将上层因素与其对应的底层综合权重相乘,得到的底层因素权重ω2=(ω11,ω12,…,ω1n,ω21,…,ωmn),归一化处理后得到ω=(ω1,ω2,…,ωn)。
通过该方法,既考虑了底层风险因素的主客观结合,又考虑了不同上层因素影响下的相对重要程度。该方法的权重使四个不同层级的风险在量化时更加准确。
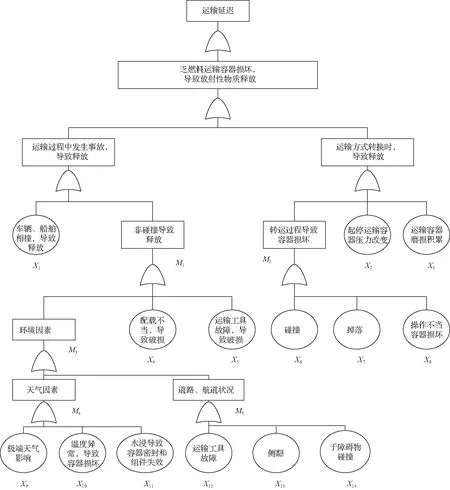
图1 故障树分析图Fig.1 Fault tree analysis diagram
1.2 评估延迟运输操作的概率
假设始发地和目的地之间的车辆行程时间范围属于区间[a,b]。车辆出发事件记为di,车辆到达事件记为dj,运输车辆到达第一个节点的事件记为dk。本文以到达第一个节点为例进行阐述,如图2所示。运输车辆从始发地A出发到第一个节点的测量时间用z表示,到达目的地的剩余时间用λ表示,λ允许的时间范围属于[c,e]。
用T(di)表示运输车辆出发时间,用T(dj)表示到达目的地的时间,T(dk)表示到达第一个节点的时间。根据图2可以看出测量时间z=T(dk)-T(di),第一个节点到目的地的剩余时间λ=T(dj)-T(dk)。因此,本文可以得到
T(dj)-T(di)=[T(dj)-T(dk)]+[T(dk)-T(di)]=z+λ,c≤λ≤e,
(1)
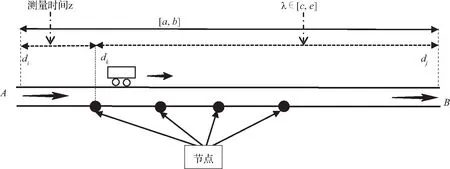
图2 运输过程图Fig.2 Transport process map
可以得到约束
z+c≤T(dj)-T(di)≤z+e,z∈[-∞,+∞],
(2)
a≤T(dj)-T(di)≤b。
(3)
一般情况下,在满足约束(2)的情况下不必再要求满足约束(3)的条件。需要注意的是,由约束(2)表示的值T(dj)-T(di)不一定都包括在由约束(3)表示的值T(dj)-T(di)的集合上。
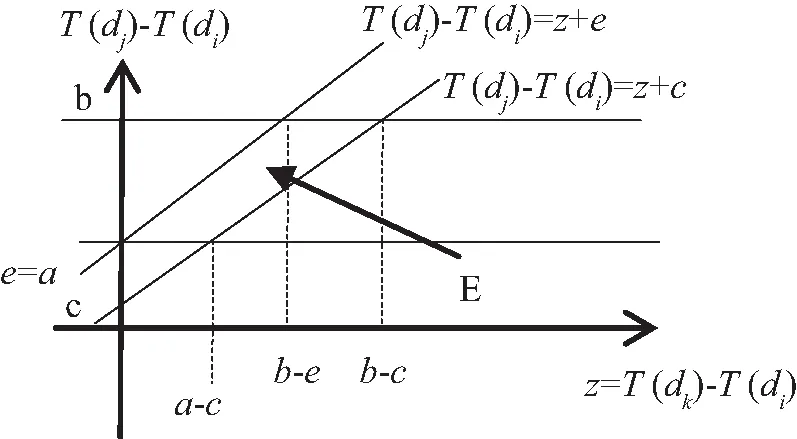
在图3中给出在满足约束(2)的情况下z与T(dj)-T(di)的集合。考虑a,b,c,e取值范围,给出e
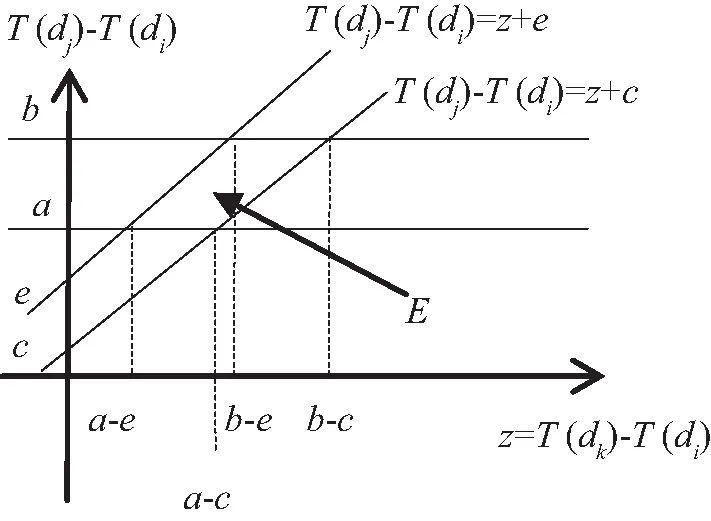
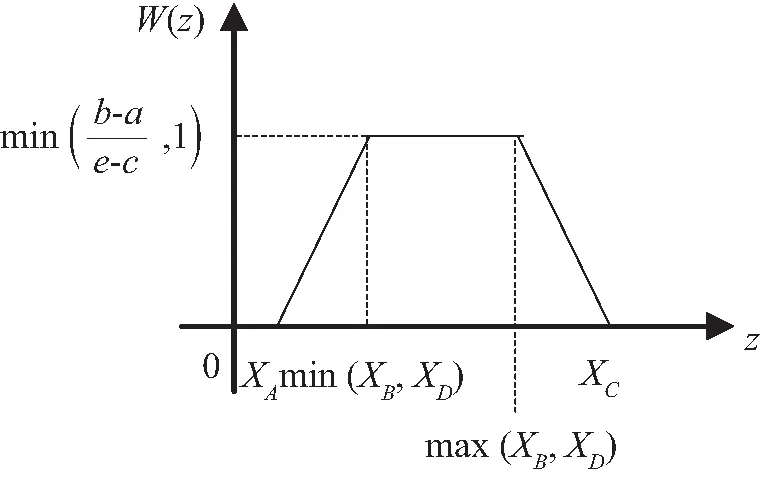
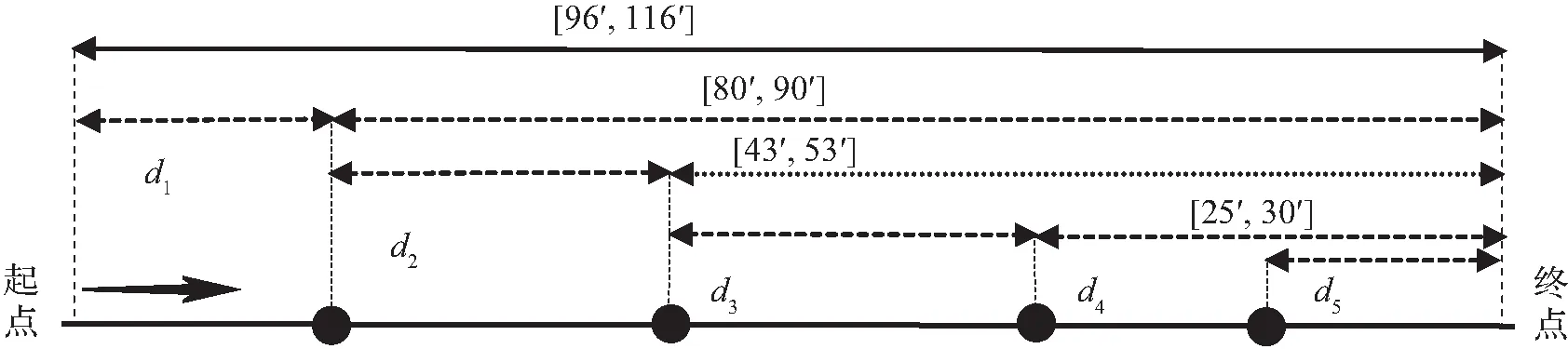
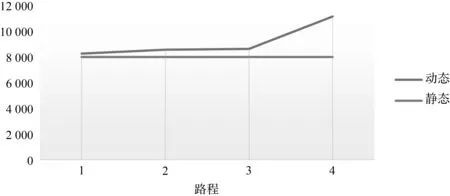
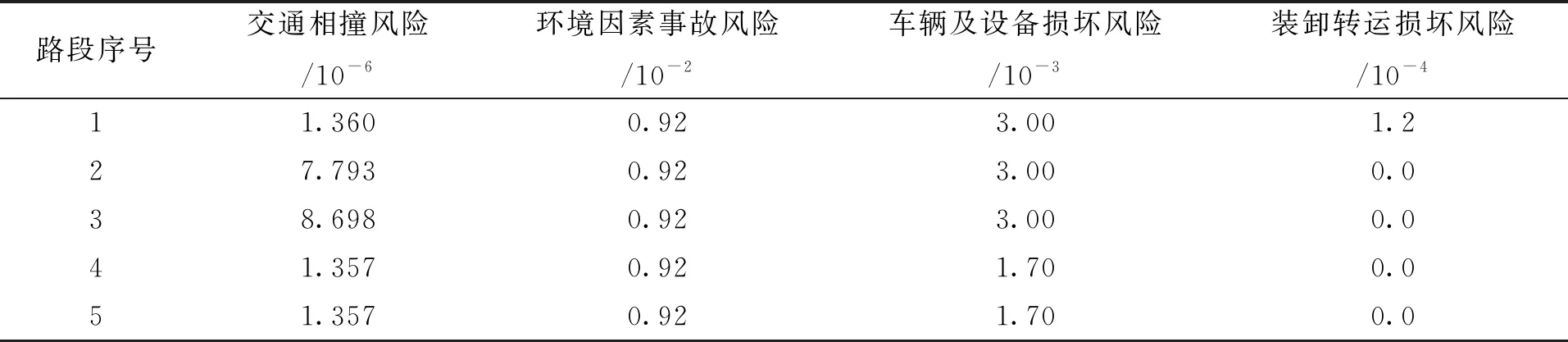
(a) e (b) e>a (c) e=a 根据约束条件可以得到以z为自变量,T(dj)-T(di)为因变量的函数关系图,其中满足条件的区域E的形状为平行四边形。E的具体形状因为点位置的不同可以分为三种情况。E的四个顶点分别为A、B、C、D,对应的坐标分别为(a-e,a),(a-c,a),(b-c,b),(b-e,b)。 然后,在持续时间T(dj)-T(di)的集合范围内对满足约束(2)的那些子集进行量化。该量化结果W为关于自变量z的满足约束的概率[13]。 (4) 在本文中,只需要考虑在XB≤XD的情况下。若XB>XD,意味着a-c>b-e,即b-a 因此,可以得到min(XB,XD)=XB=a-c,max(XB,XD)=XD=b-e。 令P=1-W,可以得到对应的关于P的函数关系式为 (5) 对应的函数W(z)与函数P(z)关于自变量z的图像如图4所示。 (a) W(z) (b) P(z)=1-W(z) 根据上述过程,可以得到动态延迟运输操作的概率P。P是根据到达节点时间z所得,所以不同阶段的动态延迟运的概率P随着节点时间z的不同而动态变化。通过故障树分析,将四种不同的风险的动态变化转变成运输延迟的动态评估。 从20世纪90年代开始,国内外学者陆续提出了众多危险品运输风险度量模型。目前,国内外在危险品运输风险评价中广泛使用定量风险评价方法,如多种危险品运输风险评价模型[14-15]、基于个人风险和社会风险运输定量风险分析的简便算法[16]、基于事故率的度量风险方法[17]。本文采用风险成本衡量路段运输乏燃料的风险,最后与前文得到的动态延迟概率相结合,使评估结果更加准确。在本文中细化了辐射泄漏所带来的损害,引用了辐射泄漏伤害公式来确定受伤人数和伤害程度。第i段路线上的量化风险Ri为 (6) 其中,Pij为第i段路程第j种运输乏燃料风险发生事故的概率;Cij为第i段路程运输乏燃料发生第j种风险发生事故时的损失。P(z)为第i段路程的动态运输延迟概率。 本文中因为四种风险对于运输的影响不同,因此对于每种风险赋予不同的权重,使评估的结果更加接近现实。ωj和pij′分别表示第i段路程发生风险j的权重和概率。Pij表示为 Pij=ωj×pij′, (7) 其中,在量化pij′时采用马尔科夫链的在时间序列上具有无后效性的基本思想,考虑了情景分析中的交叉影响概率的影响。其中前一阶段风险对某一阶段风险值的转移概率是由各风险的影响程度决定的。根据专家建议的结果,对影响的程度可按影响风险的大小和影响的正负给出影响列表如表1所示,影响程度分为七个类别。本文研究的四种不同风险其相互间的影响程度表如表2所示。阶段i下第j种风险的风险值为pij′=max[pij+ytj×p(i-1)t×pij(1-pij](1≤t≤N),其中,pij为该阶段初始概率,ytj为上阶段t风险对j风险其影响值。 表1 影响程度表Tab.1 Influence table 表2 四种风险相互影响值表Tab.2 Four risk interaction values 因为本文研究的乏燃料属于放射性的危险品,因此在考虑损失时不仅要考虑经济损失,还要考虑发生事故对于沿途人口的影响。Cij表示为 Cij=cij+Dij, (8) 其中,cij表示为第i路段发生j种风险产生的直接经济损失,Dij第i路段发生j种风险的影响人数折算成经济损失值,包括不同伤害等级需要赔偿的医疗费,抚恤金,精神赔偿金。 其中,乏燃料毒害剂量指数为 (9) 辐射泄漏的伤害率公式为 (10) Ni=∬sR(x,y)ρ(x,y)dxdy×Ri(x,y), (11) 其中α、β、λ为乏燃料泄漏相关数据拟合得到的参数,i为伤害程度,分别为轻度伤害,中度伤害、重度伤害、死亡,ρ(x,y)为人口密度。 最后可以得到i段路线上的量化风险值Ri为 (12) 通过上述的模型方法可以得到在乏燃料运输过程中各阶段的动态量化风险值。本方法充分考虑了在运输过程中风险的动态变化以及前段路程中风险对后段路程的影响。并且考虑了所运输货物乏燃料本身的特色,结合实际状况对风险进行了评估,使得到的值更加科学准确。接下来本文将通过对一个案例进行研究来验证其准确性。 根据实际情况选取了乏燃料运输车从大亚湾核电站出发到盐坝高速径心坳高架桥这段距离内进行风险的动态评估。通过比较本文采用Vissim软件进行仿真。根据道路状况和周边地形的不同,本文将该段路程划分为五段进行风险评估。其中核电站到鹏飞路公园路交叉口作为第一段测量分析路段,鹏飞路公园路交叉口到鹏飞路坪西路交叉口作为第二段,鹏飞路坪西路交叉口到盐坝高速路是第三段,高速入口到径心河大桥是第四段路程,径心河大桥到下一个高速入口为第五段路程。根据资料显示乏燃料运输车在丘陵地带的普通公路上行驶,最高车速不得超过30 km/h,平均技术车速更是低至12 km/h。并且每运行2 h或50 km就要停车检查车辆一次,每天一次全面检查,每10 d就要进行一次维护。 在利用Vissim进行仿真时,考虑到形式路段属于丘陵山地,设置的乏燃料运输车在上高速前期的速度区间为[10,14],平均速度为12 km/h。仿真得到的通过各部分的时间如表3所示。 表3 各路段仿真通过时间Tab.3 Simulation time of each section 经过多次仿真,得到通过五段路程的平均时间,具体结果如图5所示。通过仿真计算运行时间值的平均值来获得图6中所有区间的边界。车辆从核电站出发的时间为9 h。 图5 乏燃料运输过程图Fig.5 Spent fuel transportation 图6 路段五动静定量评估结果比较图Fig.6 Comparison diagram of five static and static quantitative evaluation results of section 通过查询资料和网上收集数据[18-20]可以得到各路段风险发生概率,如表4所示,相对应的四种不同的风险在各段路程所带来的经济损失和人口影响如表6所示。根据改进熵权层次分析法得到各风险的权重值分别为0.32、0.17、0.24、0.27。 表4 前阶段影响下风险发生概率表Tab.4 Probability of risk occurrence under the influence of the precious stage 表5 伤害概率拟合参数值Tab.5 Damage probability fits the parameter value 表6 风险发生后果表Tab.6 Consequences of risk (单位:元) 当通过第1段路程时,根据d1可以得到传递到其他各段路程的动态延迟概率。第2段路程的延迟概率P12(d1)=0.04,量化风险值R2=(7 877.181+29.082 58+54.513 492+0)×(1+0.04)=8 279.208。 当通过第2段路程时,可以根据d1和d2得到传递到第3段路程的动态延迟概率P23(d1+d2)=0.055,量化风险值R3=(1+0.055)×(7 819.260+42.606+60.511+0)=8 358.108。表7是根据数据模拟的从出发到第4段路程过程中,第5段路程的风险量化评估结果。 表7 路段5风险动态量化值Tab.7 Dynamic quantification value of segment risk 根据以往的定量评估模型R=P×C,可以得出第5段路程风险值为R5′=8 120.663。运输的过程是一个系统的过程,需要结合系统因素变化对一段时间内的运输安全状态进行评估,把握风险随各种因素变化而产生的变化。 本文的模型中某一阶段的量化风险值不是固定不变的,而是随着运输过程不断地发生动态变化的。在风险量化评估的过程中不止要考虑该阶段的风险状况,还要在研究过程中考虑到前期的各种风险对现阶段的影响。 在本文中,提出一种新的方法来全面量化评估运输过程中风险的动态演变。通过采用故障树来分析导致延迟的风险因素,通过评估运输延迟来实现量化前段路程风险对某一阶段风险量化的影响。在获得权重时采用改进的熵权层次分析法,降低了风险因素处于不同层级的影响,使量化结果更切合实际。采用本文的这种方法,可以使运输过程的量化结果更加准确,为多式联运路线的选择优化提供更多的支持。 随着乏燃料运输压力的不断增大,乏燃料的特殊性导致乏燃料运输的风险量化尤为重要。本文在研究乏燃料运输风险量化的过程中充分考虑了乏燃料的特性,选取的运输风险都属于对乏燃料的安全影响较大的风险。目前,我国乏燃料的运输方式也逐渐偏向于多式联运[21],本文充分考虑了多式联运过程中的转运风险,充分适应多式联运中风险的动态量化评估,更好地帮助研究人员和管理者评估和管理运输过程中的风险。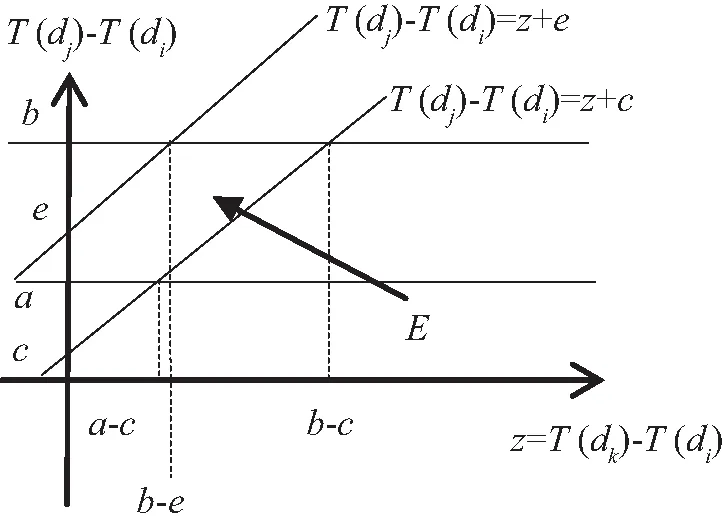

1.3 动态评估风险


2 案例分析




3 结论

