基于核密度估计的MAPSK调制信号识别

龙章勇，商晨，兰海翔，袁咏仪，刘苏扬

(1.南京铁道职业技术学院 通信信号学院，江苏 南京 210031；2.贵州大学 大数据与信息工程学院，贵州 贵阳 550025；3.贵州力创科技发展有限公司，贵州 贵阳 550018；4.贵州六盘水三力达科技有限公司，贵州 六盘水 553001)

0 引言

调制信号识别是信号盲分析、非协作通信和自适应接收等领域里的一个重要的研究方向，并且被广泛应用到电子对抗、电子侦察、自适应卫星链路设计等军用和民用领域[1-13]。特别是在卫星通信领域，建立自适应的通信链路对于通信质量的保证和星载能源的有效利用都是非常有利的。相对于高阶的正交幅度调制，多进制幅相键控(multiple amplitude phase shift keying,MAPSK)具有相近的误码性能的通信，其调制包络起伏更小[1]，所以受到广泛关注和研究[2-4]。国际空间数据咨询委员会(CCSDS组织)已经在其发布的132.1蓝皮书[5]中正式地将MAPSK调制作为自适应编码调制数据通信的主要调制方式，所以研究MAPSK调制应用价值和意义重大。

目前，已发表的研究中，关于MAPSK调制信号识别的研究很少。舒畅等[6]将MAPSK(multiple phase shift keying)和MQAM(multiple quadrature amplitude modulation)同样处理，在分析各自星座图结构和四次方谱的特点的基础上，提出基于四次方谱和幅度特征参数的调制识别算法。其算法的仿真结果表明，当信噪比大于12 dB时，其调制识别效率能达到90 %。但是该算法运算量较大，并且识别效率在信噪比不高时，识别效率较差。甘新泰等[7]对MAPSK的零中心归一化瞬时幅度谱密度最大值、四次方谱、幅度、高阶累积量等参量进行了分析，提出一种联合特征参数的信号调制识别方法。仿真结果表明,在低信噪比条件下，其识别效率比文献[6]有较大提高，但是该算法的计算复杂度和流程比较复杂，算法延迟会比较大，不利于在识别实时性要求比较高的环境中应用。

笔者提出一种基于特征提取的MAPSK调制识别算法，通过核密度估计的方法获得MAPSK调制符号的幅度分布，然后引入基于Kullback-Leibler散度(也称K-L距离)的判决器，判决输出调制模式。仿真表明，本算法的调制识别效率高，算法相对简单，性能好。

1 MAPSK调制

MAPSK调制的星座图是由多个同心圆共同组成[8]，每个同心圆均分布着多个调制符号，这些点构成的信号集如式(1)所示。

(1)

式中,Rk为第k个同心圆的半径，(2π/nkik+θk)为星座图中信号的相位，nk为第k个同心圆上的信号点数，θk为第k个同心圆上信号的初始相位，ik(ik=0,…,nk-1)为第k个同心圆上的一个信号点。在信号星座图的单个圆上的信号点都是按M-PSK进行排列的。伪格雷码映射的4+12-APSK标准星座映射图如图1所示，其中横坐标I表示实部，纵坐标Q表示虚部。在本文后续的分析中，16APSK所采用的星座参数为文献[2]中论述所推荐的参数。

对于M取值为32和64的情况下，所采取的星座结构为文献[5]所推荐的星型内外逐级递增构图，并且内外环半径都采用文献[5]中所述的推荐比例。对于32APSK，从内到外各环上的星座点数依次为4/12/16，r2/r1和r3/r1分别为2.84和5.72。64APSK标准星座映射图如图2所示，从内到外各环上的星座点数依次为：4/12/20/28，r2/r1、r3/r1和r4/r1分别为2.73、4.52和6.31。

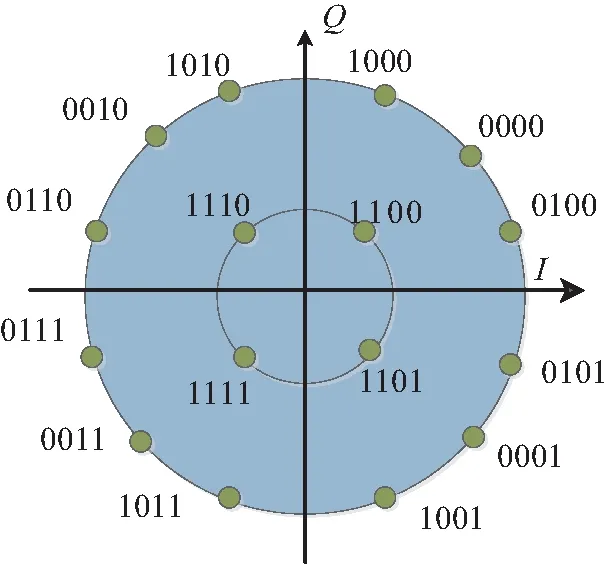
图2 64APSK标准星座映射图Fig.2 64APSK standard constellation map

2 核密度估计

核密度估计是一种新兴的非参数估计方法。给定样本数据集x1,x2,…,xn，由核密度估计公式表示的概率密度函数如下：

(2)

其中，hn为带宽因子，K(*)为核函数。常用的核函数如表1所示。

表1 常用核函数Tab.1 Common kernel functions

为了理解核函数在估计中的意义，不是一般性的，假设样本向量的获得和真正的概率密度函数p(x)，则对式(2)的估计求期望有公式(3)：

(3)

从式(3)可以看出，估计的期望为真实概率密度函数和核函数的卷积的结果。所以，带宽因子h扮演着光滑参数的角色，即当h越大，故而所得的概率密度函数越光滑。相反，当h→0时，核函数退化为冲激函数，则估计所得的概率密度函数即为真实的概率密度分布。所以恰当选择h，对估计的准确性非常重要。当h选择得过大，则会过度平滑密度函数，导致密度分布的细节信息被掩盖；当h选择得过小，则会得到非常尖锐的概率密度估计，而且稳定性较差。

估计点x处的最小均方误差可以表示为

(4)

其中PKDE(x)和P(x)分别为估计概率密度函数和真实概率密度函数[9]。由式(4)可知，最小均方误差有偏移项和方差项组成。其中偏移项为估计器的系统误差，方差项为估计器随机误差。当选择较大的h时，会减少不同样本集估计得出的结果之间的差异，即式(4)中的方差项，但会增加估计的偏移。反之,当选择较小的h时，可以减小估计的偏移，却会增加误差的方差项。

因为目前的MAPSK主要应用环境在于卫星通信领域，其所考虑的主要信道噪声为高斯白噪声，所以星座点的幅度应该是类噪声分布。故而，选择高斯核作为本文算法中核密度估计的核函数应该是最合理的。

3 调制识别算法

从前面对MAPSK的星座图的介绍可以看出，对于M取4、16、32和64时，星座图的整体结构体征并无剧烈变化。并且不同M下，星座图上最直观的变化就是“同心圆”个数的变化，也即调制符号的可能模值。基于可能模值的个数，即可判断出调制类别。

3.1 识别算法流程

本识别算法对应的调制识别模块工作在解调器的前端，这意味着该调制识别算法不需要进行载波恢复。算法流程图如图3所示，可以看出该算法主要由符号幅度提取、符号率估计、相干累积、符号幅度PDF估计、模板匹配和判决模块等部分组成。

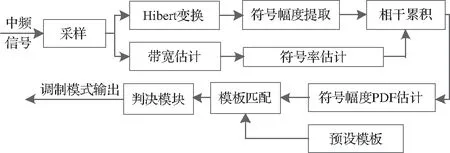
图3 算法流程图Fig.3 Algorithm flow chart

考虑在高斯白噪声信道中接收到序列为

(5)

其中，Cm,fc,fs,φ0和w(n)分别定义为发送的第m个星座符号，载波频率，采样率，初始相位和单边功率谱密度为N0的加性高斯白噪声。忽略式(5)中的噪声项，接收信号的Hilbert变换可以表示为

(6)

其中，am和bm分别表示调制符号的实部和虚部。所以对于接收到实信号的包络的绝对值为

(7)

信号的带宽估计和波特率估计部分[3]，主要是恢复符号周期，为后续的相干累加提供时钟参考。相干累计模块的作用是提高幅度提取信号的信噪比。为了提高累加的相干性，即在调制符号内相加，需要将相干累加的区间设置为半个符号长度。

3.2 基于K-L散度的判决模块

K-L散度是概率论和信息论中的常用的概念，通常用来计量两个随机分布之间差异或者随机变量之间的相似度。K-L距离在信息论中的意义为：对相同的符号集，概率分布P的随机符号分布，若用概率分布Q编码时，平均每个符号编码长度需要增加多少比特。对于离散概率分布P和Q，其K-L散度定义为

(8)

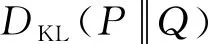
在本文提出调制识别算法中，K-L距离被用来计算估计幅度概率密度和模板幅度概率密度分布之间的距离，从而给出调制模式指示。模板幅度概率密度是在不同SNR下，备选的可能调制方式下信号的幅度分布定点化结果。将估计幅度概率密度和模板幅度概率密度之间的K-L距离存储到距离矩阵De×g中，其中下标e指示调制模式的编号，下标g指示了SNR的备选数。所以，矩阵De×g的最小值即给出了调制模式的指示和估计的SNR值。

4 仿真实验及结果分析

为了验证算法的性能，设计仿真实验：①备选的调制模式有QPSK、16-APSK、32-APSK和64-APSK；②调制模式数目e=4且SNR数目g=20；③蒙托卡罗仿真统计次数为800；④仿真验证中默认接收系统可以完成定时同步，并且定量引入误差。仿真实验结果如图4至图6所示。

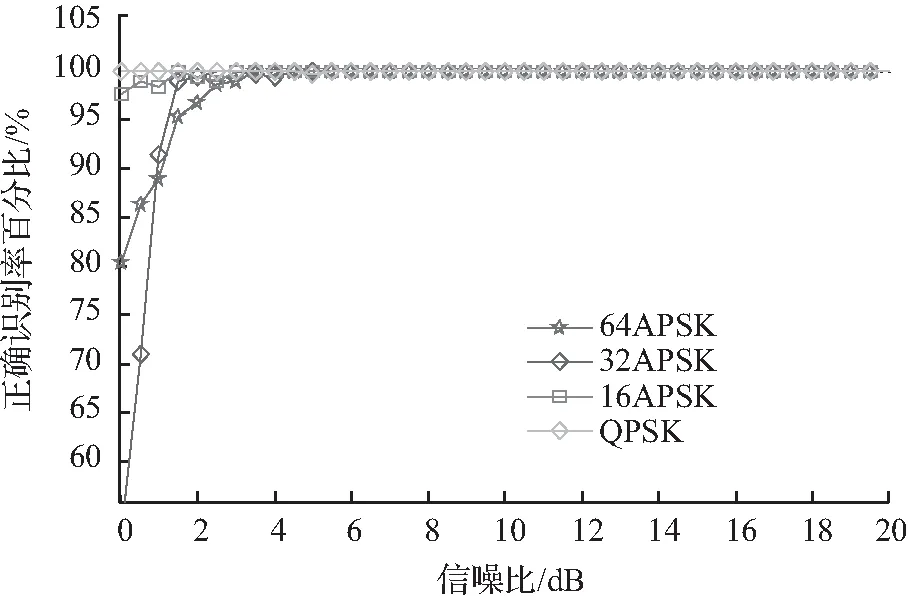
图4 不同信噪比下的识别效率Fig.4 Recognition efficiency under different SNR

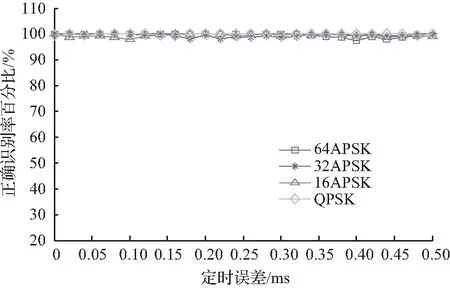
图5 不同定时误差下的识别效率Fig.5 Recognition efficiency under different timing errors

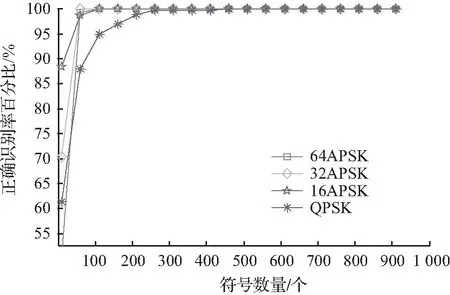
图6 不同符号数量下的识别效率Fig.6 Recognition efficiency under different number of symbols

图4中给出了在符号数量为1 000时，不同SNR条件下，算法对备选调制方式的识别效率。可以看出，在SNR大于2.5 dB时，算法对备选的所有调制方式的识别效率都达到了100 %。因为仿真实验是在符号理想同步下进行的，所以实际系统中可以肯定的是只要符号同步能完成，则识别效率可以达到仿真量级。图5给出了在SNR为10 dB、符号数目为1 000时，不同定时误差情况下算法的识别效率。从图5可知，算法对定时误差不敏感。图6中给出了在SNR为10 dB，且理想同步下，不同的符号数量对应的算法的识别效率。从图6中可以看出，当符号数目累计至250左右，算法的识别效率接近100 %。另外，算法在识别调制方式的同时，还附带给出了SNR的粗略估计。

从图4至图6中可以看出，在相同的实验条件下，调制阶数越高其识别效率越高，反之QPSK的识别效率最低。不难分析，在调制阶数越低的情况下，星座图的峰值个数越单一，所以在噪声下其“特征”越模糊，进而导致核密度估计的误差也会越大，最终导致其识别效率相对较低。

本文提出了一种基于核密度估计的MAPSK调制识别算法。对比调制模式QPSK、16-APSK、32-APSK和64-APSK，在相同的实验条件下进行仿真，从实验结果可知，本算法计算复杂度低，在SNR较低的情况下，也具有较高的识别效率；并且本算法对定时误差不敏感，算法鲁棒性好。