采用蚁群算法优化的机器人运动路径能耗模糊控制研究

许艳英，包宋建

（1.重庆科创职业学院人工智能学院，重庆402160；2.重庆文理学院电子信息与电气工程学院，重庆402160）

随着工业化和智能化的快速发展，机器人产业得到了大力推广，已应用于航天、海洋、医疗及矿山等许多领域。各个生产企业也逐步采用机器人替代人工劳动，不仅可以降低企业生产成本，而且提高了生产效率。在机器人发展的同时，其工作能力也得到了重视，不同运动路径消耗的能量差别较大。良好的路径规划不仅可以提高机器人工作效率，而且可以节约能量消耗。在购买机器人时，能量消耗是评价机器人的重要指标参数［1-2］。研究人员也开始加强对机器人路径规划方面的研究，在追求机器人负载能力的同时，使机器人运动路径最优。因此，研究机器人路径规划，对于提升机器人运动性能，减少能源消耗具有重要的促进意义。

移动机器人在搜索目标过程中，要尽可能缩短运动路径，这有利于降低能源消耗。目前，国内外许多研究人员对机器人路径规划进行了深入研究。例如：文献［3-5］研究了移动机器人路径规划模糊控制方法，在机器人末端安装了超声波传感器，通过对周围环境进行扫描探测，获取目标和障碍物信息，将信息模糊化后输入模糊控制器，经过模糊推理后得到机器人最佳运动路径。文献［6-7］研究了移动机器人路径规划人工鱼群混合算法，通过栅格法对机器人运动环境进行建模，采用人工鱼群混合算法对静态环境下的机器人运动路径进行规划，将规划结果作为遗传算法的初始种群，通过迭代寻找最优值，从而搜索到初始点到目标点的最优路径。文献［8-9］研究了机器人运动微分约束下纵横向路径规划方法，采用微分约束设计机器人可行运动路径，引入预瞄思想对机器人横向运动路径规划，能够有效地避开障碍物，从而降低实际运动路径与规划路径偏差。但是，以往研究的移动机器人运动路径消耗能量较大，从而造成了资源的浪费。对此，本文采用模糊蚁群算法优化机器人运动路径，建立了机器人结构模型，推导出机器人运动能量消耗方程式，采用蚁群算法对模糊控制器进行优化，将改进模糊控制器用于移动机器人路径规划，缩短了移动机器人搜索路径，降低了能量消耗，为深入研究机器人能量消耗提供了理论基础。

1 机器人模型

机器人模型结构如图1所示，其关节框架采用Denavit-Hartenberg（D-H）表示法。从机器人底座开始，每个关节始终围绕指定框架的z轴旋转来实现。0为机器人底部坐标系原点，4，5，6为机器人腕部坐标原点，其原点位于同一位置，称为腕部中心Pw=［PxwPywPzw］T。参数a1，a2，a3，a4，d1和d2用于描述所应用的D-H表示法中的单元之间的转换。

图1 机器人简图Fig.1 Sketch of robot

2 机器人动力学模型

2.1 运动学

采用D-H方法［10］描述机器人末端执行器变换矩阵，其关系式为

从俯视图看机器人，角度改变了机器人手腕在x-y平面上的位置，如图2所示。

图2 第1关节角度投影Fig.2 The first joint angle projection

第1个关节的角度求解表达式为

同理，可以求解第2、第3关节角度为

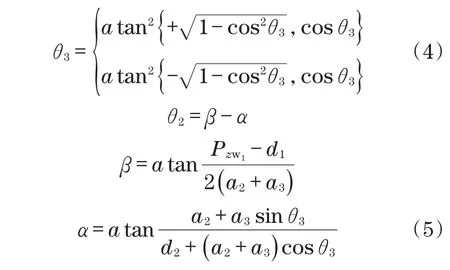
当前3个关节角度确定时，通过正运动学可以计算出腕部的旋转表达式如下：

式中：α，β，γ为欧拉角。

欧拉角度和关节角度值之间的关系式为

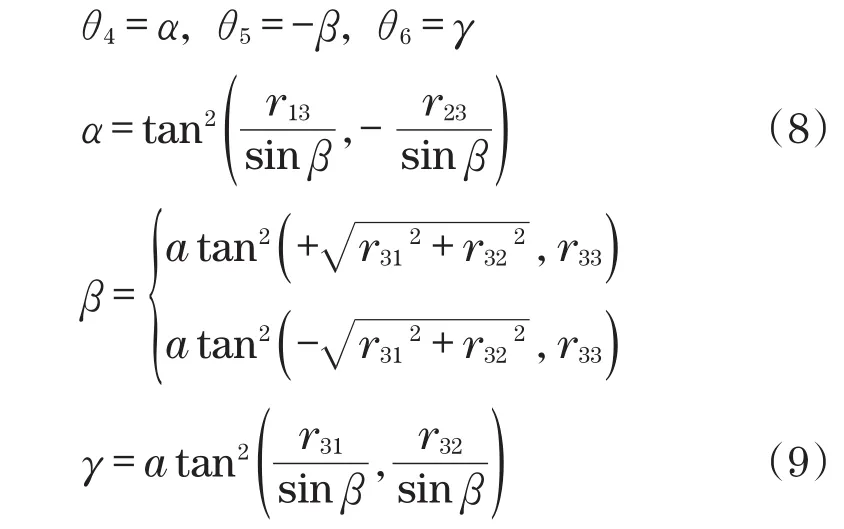
2.2 逆运动学

该过程用于获取机器人各连杆的直线运动和角度运动。从第一个连杆到最后一个连杆N=6，初始条件设置机器人底座不动，角速度ω0和角加速度α0加上线性加速度ac0都被设为0。那么对于每个连杆i的角速度ωi和角加速度αi，以及在末端的线性加速度ai和重心aci计算公式［11］为

第i个连杆重力矢量表达式为

第i个连杆的力和力矩计算表达式为

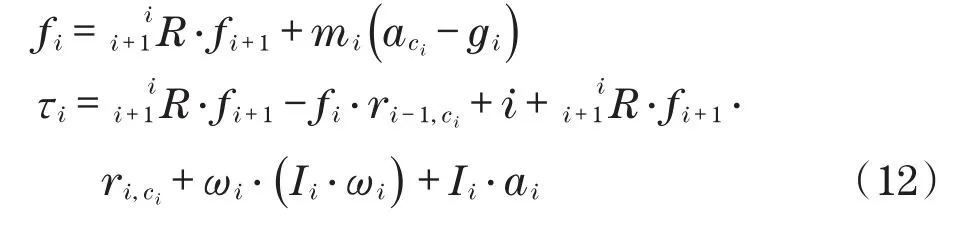
2.3 能耗计算

功率输出计算通过以下两个步骤，在特定时间间隔k内，计算出每个关节消耗的功率，对所有关节功率消耗求和，得到总功耗为

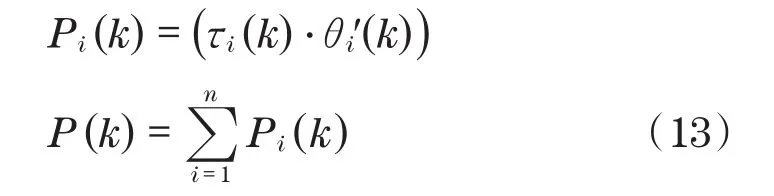
因此，能源消耗计算公式为

2.4 路径规划

为了更好地描述机器人规划路径，建立一个二维平面坐标系，栅格与编号在坐标系中的对应关系如图3所示。

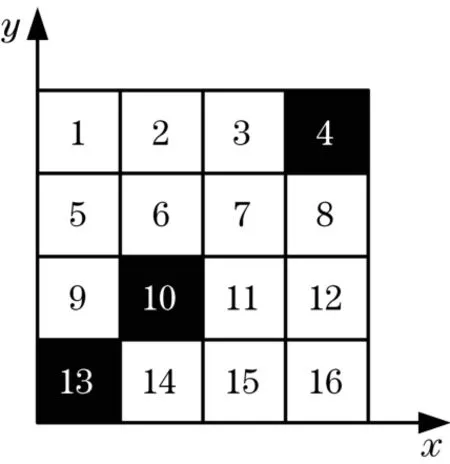
图3 栅格与编号对应图Fig.3 Corresponding graph of grid and number

在图3中，编号4，10，13为障碍物，为黑色栅格，用1表示，其他为白色栅格，用0表示。状态矩阵表示为

在栅格中，坐标编号构成的映射关系［12］为

式中：n为坐标系中的编号；Nx，Ny分别为每行格数和每列格数；mod（n，Nx）为n/Nx的余数；ceil（n/Ny）为n/Ny的整数。

任意两个栅格之间的距离为

为了方便描述，假设蚂蚁集合为ant=｛1，2，···，M｝，M为蚂蚁总数，蚂蚁的移动路径结构如图4所示。由于序号4，10，13为障碍物，蚂蚁无法通过，所以没有箭头。

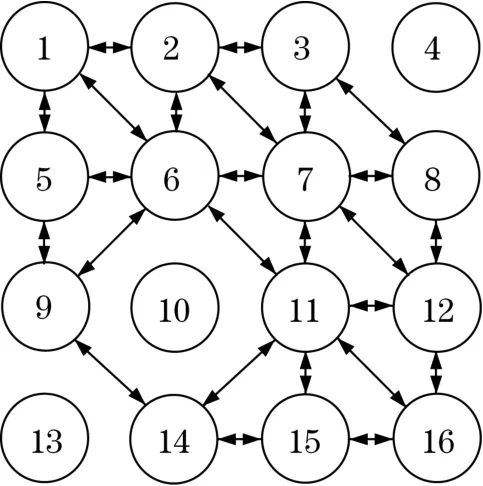
图4 蚂蚁路径结构Fig.4 Ant path structure

3 模糊蚁群算法

3.1 模糊控制器

假设机器人末端执行器为原点，半径区域为r。当机器人半径区域与障碍物交集不等于空集时，判断输出为1，即前面有危险；否则输出为0，前面没有障碍物，即为安全区域。

坐标误差方程式为

式中：xg，yg为目标位置坐标。

本文设置了9个模糊区域，如图5所示。

图5 模糊区域Fig.5 Fuzzy area

对图5模糊区域进行线性化处理，将误差（ex，ey）分为｛N，Z，P｝，模糊输出动作角（θf1，θf2）分为｛N，P｝。为了保证机器人能够避开障碍物，采用如下隶属度函数［13］：

式中：ex，θf1的隶属度函数与ey，θf2相同，只需分别将ex，θf1改成ey，θf2即可。

假设误差（ex，ey）处于（N，N）位置时，当判断输出为1，则有遇到障碍物，移动机器人负向动作θf1（t）=N，正向动作θf1（t）=P，从而实现避障动作。当判断输出为0，则处于安全区域，则机器人正向动作，朝向目标位置前进。采用不同模糊规则，可以完成机器人不同路径规划和避开障碍物行为。

3.2 模糊控制优化

采用蚁群算法在线优化模糊控制器，以期望机器人不仅运动路径最小化，而且成功避开障碍物，从而节约能量消耗，其优化流程如图6所示。

模糊规划期输出函数为

式中：S为障碍物判断输出值；k=［k1（t），k2（t）］T为蚁群校正参数；f（ex，ey，S）=［k1（t）θf1（t），k2（t）θf2（t）］T为模糊规划函数。

移动机器人根据目标位置（xg，yg），对实际位置（x，y）做出调整，判断外部是否有障碍物，规划出机器人各个关节模糊动作角度θf1（t），θf2（t）。并且，蚁群算法根据最优路径，对动作角度进行在线优化，得到最优动作角，从而完成机器人相应动作。

图6 模糊控制器优化流程Fig.6 Optimization process of fuzzy controller

4 仿真及分析

为了对比不同控制方法的机器人能量消耗，机器人分别在环境1、环境2和环境3中移动，如图7、图8和图9所示。采用Matlab软件对不同环境能量消耗进行仿真，栅格规模为n=8×8，蚂蚁数量为m=20，仿真时间为1 s。机器人在不同环境中消耗的功率分别如图10、图11和图12所示。

图7 环境1移动路径Fig.7 Path of movement in the first environment

图8 环境2移动路径Fig.8 Path of movement in the second environment

图9 环境3移动路径Fig.9 Path of movement in the third environment

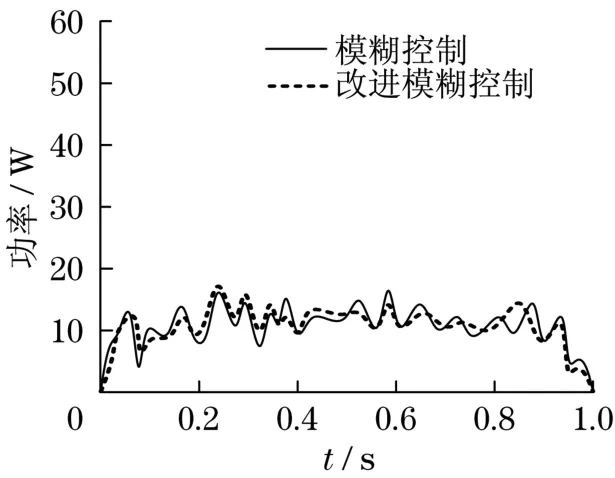
图10 环境1消耗功率Fig.10 Power consumption in the first environment

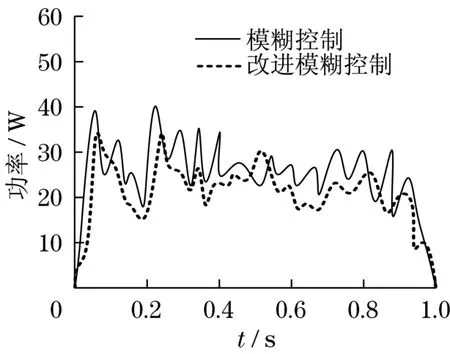
图11 环境2消耗功率Fig.11 Power consumption in the second environment

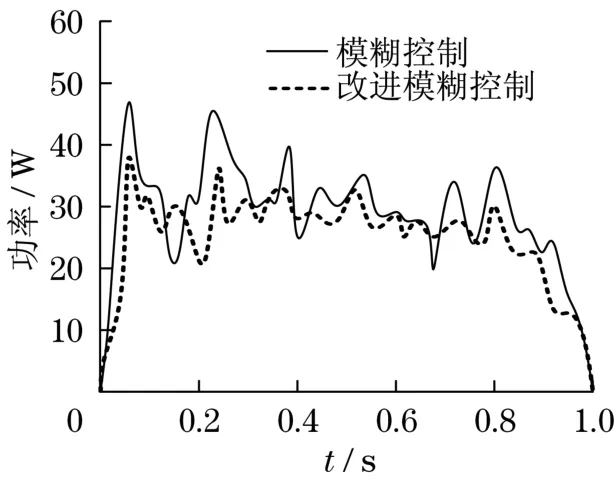
图12 环境3消耗功率Fig.12 Power consumption in the third environment

在图7中，两种控制方法输出功率几乎相同，主要原因是障碍物较少，分布相对简单。图9比图8障碍物多，而且分布也相对复杂，随着障碍物的增加和分布变得更加复杂时，移动机器人输出功率就会增大。在图7和图8中，改进模糊控制方法能够搜索到最优路径，减少运动位移，从而降低输出功率，节约能源消耗。

由图10可知，机器人在环境1工况下运动，采用模糊控制方法和改进模糊控制方法输出功率几乎相同。由图11可知，机器人在环境2工况下运动，采用模糊控制方法输出最大功率为40 W，而采用改进模糊控制方法输出最大功率为34 W。由图12可知，机器人在环境3工况下运动，采用模糊控制方法输出最大功率为47 W，而采用改进模糊控制方法输出最大功率为38 W。

5 结论

本文建立了机器人动力学模型，对移动机器人进行路径规划，采用蚁群算法优化模糊控制器，对比不同环境下移动机器人运动消耗功率，主要结论如下：①在相同的路径下，环境1障碍物较少，其消耗的功率较少，而环境3障碍物较多，其消耗的功率最大，障碍物越多，分布越复杂，消耗的功率也越多；②采用蚁群算法优化模糊控制器，可以使移动机器人搜索到最优路径，移动机器人运动路径变短，其功率消耗也随之减少，从而节约了能源；③采用Matlab软件对机器人不同控制方法运动路径能源消耗进行仿真，可以对比出改进模糊控制方法明显优于模糊控制方法，为深入研究机器人路径规划能源消耗提供参考数据。