基于流场分析的压裂四通管汇冲蚀预测
刘 鸣,张 川,蒋发光,林 勇,张 敏,李 昕
(1.四川宝石机械钻采设备有限责任公司,四川 广汉618300;2.西南石油大学 机电工程学院,成都610500)①
近年来,非常规油气开发取得了突破性进展,压裂技术成为关注的焦点,重要性日益凸显,在页岩气、致密气和致密油等非常规油气的开发中发挥着重要的作用。压裂车所提供的高压压裂液由于受力不均的影响,其波动不可避免[1]。当压裂液进入高压管汇时,将会引起高压管汇的剧烈振动、冲蚀等问题。引起管路振动的原因与管路的布置、流入流出角度、弯头半径等因素有关,同时这些因素对管汇系统的压力、流场分布以及内壁冲蚀影响大,可能导致现场作业安全性、管汇系统寿命降低。
Zhang Y 等[2]考虑颗粒撞击前后近壁区域的颗粒尺寸效应,将计算出的固体颗粒侵蚀模式与试验数据进行比较,研究计算颗粒碰撞速度模型的准确性。赵云婷等[3]借助散相模型,计算了喷砂器结构在不同速度、含沙量下的最大冲蚀磨损量,并根据最大冲蚀磨损量计算出了对应管道的最大冲蚀磨损量,预测维修时间。肖益民等[4]利用欧拉双流体模型,借助Fluent软件,对Y 型喉管内气固两相流进行数值仿真,研究了颗粒不同入射角对喉管内流场的影响,得到压降与入射角之间的关系曲线以及喉管内改进前后的流场情况。李永乐等[5]基于k-ε 湍流模型和Simplec算法,对中石化某管线单级双吸输油泵的全流场进行了数值模拟,得到了其压力、速度分布。李静等[6]对不同雷诺数和不同半径比下90°圆弧弯管内的流体流动进行了数值模拟,分析了管内流体的速度场分布、压力场分布以及二次流现象。Zhang JiXin等[7]揭示了三通接头冲蚀的特点和破坏机理,通过计算流体力学模拟对三通接头的宏观特征和扫描电镜(SEM)图像进行分析,得到了不同流量类型三通接头的侵蚀分布,定义了三通接头的失效模式和失效机理。刘洪斌等[8]研究了压裂高压管汇在大排量携砂液输送过程中的管壁冲蚀磨损问题,基于数值模拟计算,研究了冲蚀发生机理及位置,探讨了高压管汇的冲蚀特点。张逾等[9]进行了正弦屈曲管柱液固两相环空流动及冲蚀数值预测,研究了颗粒撞击速度与角度对冲蚀速率的影响,为准确预测环空压裂过程管柱冲蚀损伤提供了理论依据。
笔者开展了高压压裂管汇的流场及冲蚀模拟,对在冲蚀作用下的管汇的寿命进行预测。并对端流速下的内部流场进行了数值模拟,分析了流场内流速和压力参数的变化情况、流场对四通管道造成的影响、入口端流速及陶粒粒径对弯管冲蚀行为的影响;验证了四通结构处较易腐蚀的部位。
1 压裂管汇分析模型建立
本次所研究的压裂管撬如图1所示。为能实现10台泵联合工作的压裂管汇,采用直通结构衔接泵出口管与汇管。

图1 压裂管撬示意
应用FLUENT 软件研究四通管路内流场与冲蚀。首先对实物模型进行必要的简化,选取图1框线部分的四通结构,该处共有3个入口1个出口,v1处为前端6 台压裂泵的综合入口,v2、v3为两台独立压裂泵入口,出口为8台压裂泵的综合出口。所建立的四通管道结构与网格模型如图2所示,网格模型采用六面体网格进行划分。

图2 四通管道结构与网格模型
分析模型中,主要参数与条件为:①主通径130 mm(5⅟8英寸),侧通径69.85 mm(2■8英寸);②介质为压裂酸化液、携砂液等;③紊流模型为k-epsilon;④最大排量14.63 m3/min;⑤砂比0~28.1%;30/50目陶粒29.1 m3,20/40目陶粒8.3 m3,携砂液275.5 m3(体积比9.3%的陶粒的粒径300~600 μm,体积比2.65%的陶粒的粒径425 ~850μm);⑥陶粒密度ρ=1 200~1 750 kg/m3;⑦最大流速12.2 m/s,即v2max=v3max=12.2 m/s。
利用等效流量计算管路等效速度的机理,计算分析模型的综合入口速度条件。由式(1)计算得到综合入口(inlet1)处最大流量Q1=14.63 m3/min,则v1max=Q1max/60S1max=17.86 m/s。

式中:Q1为综合入口端流量,m3/min;v2、v3为入口2、3端流速,m/s;S1、S2、S3分别为入口1、2、3端截面积,m2。
2 压裂管汇四通冲蚀分析
研究不同入口流速、陶粒粒径和陶粒密度对冲蚀速率的影响,求出工况条件下的最大冲蚀速率;在此基础上研究危险工况下四通管汇冲蚀后的不同管壁内径对冲蚀速率的影响,求出开始工作到最大允许冲蚀之间的平均最大冲蚀速率。
2.1 不同流速对冲蚀的影响
取陶粒粒径(850μm)、密度(1 700 kg/m3)作为固定参数,取四通入口流速v=2 ~12.2 m/s作为变量,分析不同入口流速对冲蚀速率的影响,计算结果如图3所示。
由图3可知,不同入口流速下易冲蚀区域的分布基本一致,主要分布在接近四通交汇处的出口管区域;冲蚀的范围随着入口流速的增大而减少;冲蚀速率随着入口流速的增大而增大,入口流速12.2 m/s时的最大冲蚀速率是入口流速2 m/s时的149倍。
2.2 不同粒径对冲蚀的影响
为研究不同陶粒粒径d 对冲蚀的影响,取陶粒粒径d 为300~850μm(密度1 700 kg/m3、入口流速12.2 m/s),分析结果如图4所示。
由图4可知,不同粒径下的易冲蚀区域分布基本一致,冲蚀集中在接近四通交汇处的出口管过渡区域;冲蚀速率随着陶粒粒径的增大而增大;粒径从300 μm 增大到850μm 时,最大冲蚀速率增大1.38倍,故选择陶粒支撑剂时应考虑过大粒径对冲蚀的影响。

图3 不同流速对冲蚀速率的影响
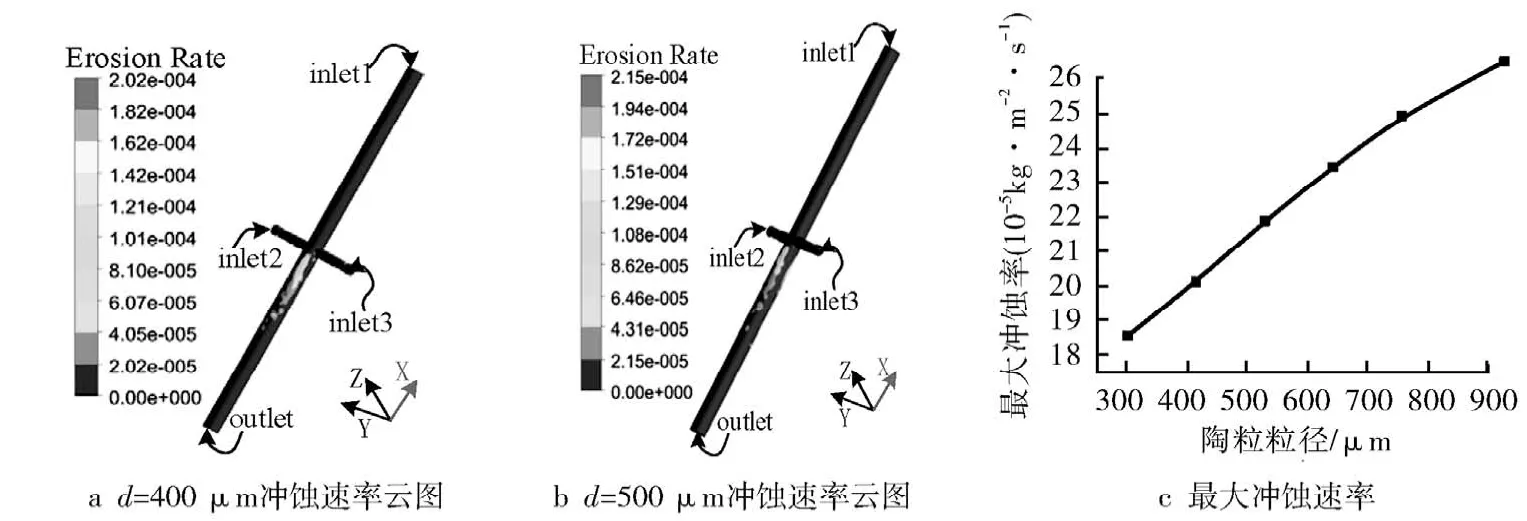
图4 不同陶粒粒径下的冲蚀速率分布
2.3 不同陶粒密度对冲蚀的影响
为分析陶粒密度对冲蚀速率的影响,取陶粒的密度ρ=1 200~1 750 kg/m3(粒径850μm、入口流速12.2 m/s),分析结果如图5所示。

图5 不同陶粒密度下的冲蚀速率分布
由图5可知,冲蚀速率随着陶粒密度的增大而增大,当陶粒密度从1 200 kg/m3增大到1 750 kg/m3时,最大冲蚀速率增大1.45倍,故选高密度压裂液时要注意对冲蚀的影响。
2.4 不同管径对冲蚀的影响
流体冲蚀会导致压裂管汇四通的内管壁减薄,故需研究不同四通出口管内径对冲蚀速率的影响。取四通出口管的外径R=105 mm,内径r=65 mm,内压pi=90 MPa,外压po=0。由拉美公式计算得出3个主应力后,由第三强度理论求得Mises等效应力σs[10]。

不同内径下四通的等效应力如图6所示。若取材料屈服强度为789 MPa,且许用应力小于材料屈服强度的0.9 倍,计算得到四通的最大许用内径rmax≤84 mm。

图6 四通不同内径下等效应力
分析得到冲蚀后不同出口管内径rs对冲蚀速率的影响如图7所示。不同出口管内径下的易冲蚀区域的分布基本一致,分布集中在接近四通交汇处的出口管区域;冲蚀速率随着出口管内径的增大而减小,且当内管壁从65 mm 增大到84 mm 时,最大冲蚀速率减少了0.99倍。图7拟合出了最大冲蚀速率与出口管内径的线性关系,开始冲蚀到管汇冲蚀安全程度的平均最大冲蚀速率为7.99×10-5(kg·m-2)/s。


图7 不同内径下的四通冲蚀速率
3 压裂管汇四通寿命评估
3.1 压裂四通管汇寿命理论
由冲蚀速率U 的定义可知,四通压裂管的冲蚀速率为管壁单位面积、单位时间内损失的管壁材料质量。从定义上利用冲蚀速率U 推导出管壁的质量损失MS,同时利用冲蚀磨损造成的管壁体积损失V 与管壁材料密度ρ 的乘积得出质量损失MS,并将两种质量损失MS等价,从而得到剩余寿命模型。采用剩余寿命模型,并结合允许壁厚损失X 和FLUENT 软件联合求得的最大冲蚀速率U,计算出压裂四通管汇的使用寿命T。
3.2 压裂四通管汇使用寿命预测
易冲蚀位置出现在压裂管接近四通交汇处的出口管区域。按照理论模型及相关管道寿命公式[11]对压裂四通管汇的出口管的使用寿命T 进行推导,将冲蚀速率转化为质量损失。

式中:MS为压裂四通管汇的管壁质量损失,kg;U为冲蚀速率,kg/(m2·s);S 为冲蚀处压裂四通管汇的内壁表面积,m2;T 为压裂四通管汇的使用寿命,min;rc为冲蚀前压裂管的内径,m;rs为冲蚀到允许程度后压裂管的内径,m;L 为冲蚀的压裂管长度,m。
质量损失MS为:

利用压裂四通管汇的管壁体积损失与压裂管材料密度的乘积得出质量损失。
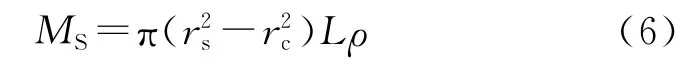
式中:ρ为压裂管材料的密度,kg/m3。
结合式(5)和(6),得出剩余寿命为:

式中:X 为压裂四通管汇的允许壁厚损失,m。取管汇材料密度ρ=7 850 kg/m3,则:

由式(8)可得,冲蚀速率、允许壁厚损失与使用寿命关系曲面如图8所示,压裂四通管汇的使用寿命随着冲蚀速率U 增大而减小,随着允许壁厚损失X 的增大而增大。
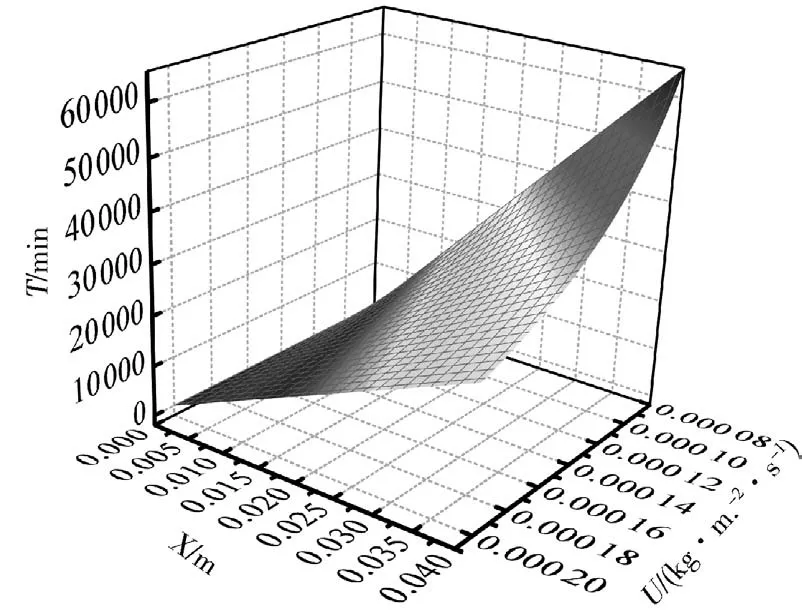
图8 冲蚀速率、允许壁厚损失与使用寿命关系
将压裂四通管汇的允许壁厚损失X(0.019 m)和最大平均冲蚀速率(7.99×10-5kg/(m2·s))带入式(8),求得压裂四通管汇的最小使用寿命为31 111 min。
4 结论
1) 冲蚀速率随着入口流速、陶粒粒径和陶粒密度的增大而增大,入口流速从2 m/s增大到12.2 m/s、陶粒粒径从300μm 增大到850μm 和陶粒密度从1 200 kg/m3增大到1 750 kg/m3时,最大冲蚀速率分别增大149倍、0.38倍和0.45倍。在选择粒径、密度较大的支撑剂时应注意其对管道冲蚀的影响;冲蚀速率随着冲蚀后出口管内径的增大而减小,当内径从65 mm 增大到84 mm 时,最大冲蚀速率减少了0.99倍。
2) 各种工况下易冲蚀区域出现在四通交汇处的出口区域,分布基本一致。
3) 在得到既定条件下,预测压裂四通管汇的最小使用寿命大于30 000 min。

