基于RSM 模型的油-水旋流器单相流场特性模拟研究

艾贤明，华卫星，张起欣，李 江，管金发，周 毅

（1.中国航空油料西北公司，西安710082；2.陆军勤务学院 油料系，重庆401311）①

旋流器是油水分离的主要设备，旋流器内流场的流动属于强湍流运动［1］。目前，对湍流的理论研究还不能和层流相比，只能通过模型假设来对旋流器的流场进行预测［2-4］。为了确定粒子在旋流器内的运动轨迹，探明速度、压力等流场特征，本文采用RSM 模型，对油-水旋流器的单相流流场的特征进行模拟研究。

1 模型的建立

1.1 网格划分

网格质量的好坏直接影响数值模拟的准确性，得到高质量网格的原则为：网格单元的稳定性好，即在三维空间里，六面体的数量和质量较高；网格的正交性好且较为光滑；在湍流度强、雷诺数高的地方要有充分的网格点，避免出现漏选的情况发生［5-8］。

采用前处理软件Gambit对旋流器模型进行网格划分。网格的划分决定了计算的精度，分别对0.1、0.5和1.0等不同网格尺度进行尝试，最终得到了一个合适的模型。该模型包括353 421 个节点、988 612个网格和2 114 010个面，如图1所示。

图1 旋流器网格划分

1.2 初始边界条件

通过设置初始边界条件，与选用的模型相结合，可以使方程组成为定解问题。初始边界条件的设置要尽量与实际情况相关，尤其是在这种复杂的流动情况下，要求更加严格。本文采用时均方程，只需对边界条件进行设置，通过改变边界条件，可以得到不同情况下的模拟结果，相比试验而言，具有方便、高效的优点。旋流器初始边界条件主要有入口、出口和壁面等［9-11］。

1.2.1 入口边界条件

旋流器入口采用速度入口边界，来流流体为标准状态下的水，假设入口处的湍流已经充分发展，入口处湍流强度设为5%，按式（1）计算［12-14］。

式中：I为入口湍流强度；u′为湍流脉动速度；u 为平均流速；ReDH为管流雷诺数。

由于来液流动方向与进口边界垂直，采用速度入口。

式中：k为紊流脉动动能；ε为紊流脉动动能的耗散率；Cμ为黏性系数；lm为水力直径。

1.2.2 出口边界条件

假设流体在出口处湍流已达充分发展状态，出口边界选用压力出口边界，采用第二边界条件为0，作为出口边界条件［15］。

式中：ur为流体线速度；uθ为流体角速度；uz为流体轴速度。

出口的边界条件一般由于与外界大气直接相通，可以作为自由出流条件来进行计算。

1.2.3 近壁面条件设置

1.3 模型假设

通过对数学模型的分析和物理模型的选择，进行以下假设：①水相为连续稳定的，不存在任何密度和状态的变化；②油相为均匀分布的球状颗粒，可以受到离心力作用，没有发生团聚、破碎和乳化的现象；③分离过程中外界的温度不变；④分离过程中，

湍流是一种黏性有旋流动，在壁面上切向速度为0，液体与壁面无滑移；在法线方向上，液体速度都为0。尤其在近壁面根据边界层理论，由于黏性力的作用，对于本文所选的水，设定为无滑移条件，壁面边界条件为［16］：各组分的尺寸没有发生变化。

1.4 模拟过程及分析

选择雷诺应力模型进行模拟，在边界条件设置好的情况下，残差数量级设为10-6，经过1 800步的迭代，方程收敛。残差收敛过程如图2所示。

由图2可知，各个参数随着迭代次数的不断增加，残差也不断减小，并且下降曲线也比较平滑，证明了模拟过程较为合理，能反映真实的流动情况。

图2 残差收敛过程

为了增加模拟结果的直观和分析的方便性，分别取溢流段、圆柱段、大椎段、小锥段和底流段上的截面作为分析对象，如图3所示。

图3 旋流器的数据采集截面

2 单相流流场模拟

2.1 流场的运动轨迹

旋流器的内流场的运动轨迹如图4所示。

从图4可知，在旋流器内的流场中，随着流体的流动，产生旋转流，并在旋转力场的作用下，自动地分为内外2个螺旋，外螺旋方向向下，内螺旋方向向上；大部分的流体都从外螺旋中经底流口流出，只有少部分的流体从内螺旋经溢流口流出。

图4 旋流器内流场流线云图

2.2 速度场特征

以上述旋流器作为模拟对象，设置入口速度为17 m／s，旋流器中x=0和z=0.005截面上的速度矢量如图5～6所示。

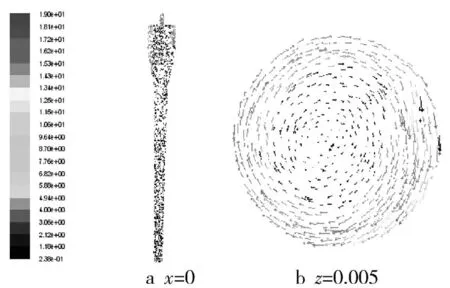
图5 x=0和z=0.005截面上的速度矢量云图

图6 旋流器的三维速度矢量云图

从图5中可以看出，因为单入口造成的不对称性，在流场中不同区域的流动也不同，特别是在圆柱段和大锥段，可以清晰地看出，内流场并不沿着旋流器的几何轴心对称。从图6中可以得到，入口处的速度场数值明显大，且所占的区域广。随着在旋流器中的流动，数值不断减小，影响区域也减小，从而在截面中留下了近似椭圆形状的速度等值图。

2.3 切向速度

在旋流器的流场中，切向速度是离心力场产生的，而且数值也远大于其他两向的速度。从理论上讲，旋流器内的切向流动应该等同于理想流场中的强制涡与自由涡的组合运动，但是由于流动空间的受限，以及特殊结构的影响，旋流器内仅在外围区域形成了准自由涡流动，而在轴心附近则可视为强制涡。

旋流器内流场各位置段的切向速度如图7～10所示。

图7 溢流口与圆柱段切向速度对比

从图7可以看出，在溢流口处的流体切向速度数值较小，在2 m／s以下，且从轴心向器壁方向，切向速度先增大后减少，但是整体情况比较平稳，说明了溢流口内的流体在流出旋流器时，基本上已经进入了比较稳定的状态。在圆柱段的流体切向速度数值就比较大，最大值达到了12 m／s，而且随着径向位置的变化，数值变化也比较大，从轴心向器壁方向，切向速度先增大后减小，再增大至最高值，最后变为0，说明了流体在圆柱段的运动比较复杂，受到的各种作用力也比较多，导致运动速度的变化也比较大。

图8 圆柱段与大锥段切向速度对比

从图8可以看出来，大锥段内的流体切向速度相对较小，基本上都在10 m／s以下，且随着半径的增加，切向速度先增大，在快接近壁面时达到最大值，最后迅速减小到最小值，说明了大锥段内的流体切向运动是对称的，沿着固定的规律运动。与圆柱段相比，流体的切向运动就比较规律，且运动的范围和剧烈程度都有所下降。

图9 大椎段与小锥段切向速度对比

图10 小锥段与底流段切向速度对比

从图9中可以看出，小锥段内的流体切向速度较小，最大值未达到3 m／s，特点也是沿着轴心到壁面的方向先增大后减小，比较对称，说明了流体在此处的切向运动已经比较平稳。与大锥段相比，流体的切向运动除了在范围和数值上比较小，其他都较为相似。

从图10可以看出，底流段内的流体切向速度比较平稳，基本上在2 m／s以下，随着半径的变化也没有太大的波动，说明流体在这里已经进入了平稳阶段，正常流出底流口。与小锥段相比，流体切向运动大大减小，变化趋势也更加微弱，底流段的流体主要是轴向运动，与实际情况比较一致。

3 结论

1） 旋流器内流场在不同位置的切向速度是呈缓慢地变化，随着轴向位置的下降，切向速度受径向位置的变化影响越来越大。

2） 流场的对称性对旋流器的工作效率也有很大影响。双入口旋流器流场在对称性和分离效率上要好于单入口旋流器，但是迫于成本、安装等问题，单入口的旋流器应用更加广泛。

3） 在溢流口下的区域内，流场的对称性比较好；在锥段下半部分和接近底流口的位置，对称性就比较差，其原因可能是由于流道变化导致的湍动能加强造成的。