线性交替的双数列通项问题揭秘*
福建省惠安第三中学
一、线性递推数列模型的内涵与外延
对于满足:an+1=kan+b(n ∈N*,k0)的数列{an},因其前后项关系类似于函数y=kx+b(0),故常称之为线性递推数列.这样的递推关系模型涵盖了多种常规数列:
(1) 当b=0时,an+1=kan(n ∈N*,k0),{an}为等比数列;
(2) 当k=1时,an+1=an+b(n ∈N*),{an}为等差数列;
(3) 当10时,an+1=kan+b可配凑为的形式,说明{an+c}是首项为a1+c,公比为k的等比数列.
值得一提的是,很多复杂递推关系模型往往是由“an+1=kan+b”变式替代而来的:当数列{an}的通项an表示某一数列{bn}的前后项关系时,比如说an=pbn+1+qbn(p,q为非零常数),将此代入an+1=kan+b中就得到bn+2,bn+1,bn的关系.反之,给定bn+2,bn+1,bn的线性递推关系,我们一般可通过恰当的配凑变形、构造转化为常规数列来求解.应该说,诸如这类“由某一数列前后几项线性关系构造新数列求通项”的问题中,其递推关系模型往往来源于对“an+1=kan+b”的迭代或转型.
当数列{an}的通项an表示某两数列{bn},{cn}的通项关系时,比如说an=pbn+qcn(p,q为非零常数),将此代入an+1=kan+b中就得到bn+1,bn,cn+1,cn的“混合”关系,这其实就是双数列的递推关系,其中数列{bn}和{cn}之间可能是独立(彼此无关)的,也可能是交错(彼此相关)的,据此我们可初步领略到那些双数列线性递推问题的生成根基.
二、线性交替递推关系的代换与变式
很多线性双数列通项问题的求解关键是围绕“双数列的线性组合”来构造常规数列的.
例1(2019年高考全国ⅠⅠ卷理科第19题) 已知数列{an}和{bn}满足a1=1,b1=0,4an+1=3an-bn+4,4bn+1=3bn-an-4.
(Ⅰ) 证明:{an+bn}是等比数列,{an-bn}是等差数列;
(ⅠⅠ) 求{an}和{bn}的通项公式.
解析将4an+1=3an-bn+4和4bn+1=3bn-an-4两式分别进行相加、相减,化简整理易得:2(an+1+bn+1) =an+bn,an+1- bn+1=(an-bn)+2.故{an+bn}是以a1+b1=1 为首项、公比为的等比数列an+bn=且{an-bn}是以a1-b1=1 为首项、公差为2的等差数列,an-bn=2n-1(n ∈N*).从而有

点评这道全国高考题并不难,但却给我们暗示了:线性双数列通项问题可通过“双数列的线性组合”来构造常规数列,数列{an+bn},{an-bn}中的递推关系可分别看作是由常规的代换得来的,4an+1=3an-bn+4,4bn+1=3bn-an-4 其实就是常规数列{cn},{dn}相关关系的隐形变式.
例2(2019年福建单科质检理数B卷第16题) 已知数列{an}和{bn}满足且a1=1,b1=0,则a2019=____.
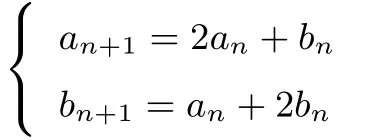
解析类似上题,发现上述关系中数列{an}和{bn}的第n+1 项系数相同,第n项系数交替.将两式进行相减恰得an+1- bn+1=an - bn(n ∈N*).又a1- b1=1,故有an - bn=1(n ∈N*).将两式进行相加得an+1+bn+1=3(an+bn)(n ∈N*),则 有:an+bn=(a1+b1) ·3n-1=3n-1(n ∈N*).再由解得故有
注记本题也可将an - bn=1 再代入得an+1=进而得到:an-
例3(2019年百校联考理科第12题) 已知数列{an}和{bn}满足:令cn=an -bn,则的n最小值为
A.9 B.10 C.11 D.12
解析注意到本题递推关系中“bn+1”可 由代换,从而得到的形式,两式作差得an+1-bn+1=即故得等比数列{cn}的通项公式由0.9·解得n ≥10.
点评不难发现,若将两式相加可得an+1+bn+1=an+bn=1.3,进而求出数列{an}和{bn}的通项公式;在上述三个例题的线性递推关系中,均明显具备“后项系数交替”的特征,故对数列{an}、{bn}直接进行“和差组合”即可发现、构造新的常规数列.
例4(2017年福建省单科质检理科第12题) 已知数列{an}和{bn}满足:a1=b1=1,an+1=an+2bn,bn+1=an+bn,则下列结论正确的是( ).
解析根据选择支数列结构特征,可猜想的通项公式是判断本题的关键点.故在

三、线性交替递推关系的配凑与构造
上述例题中,数列{an}和{bn}均有明确提供线性组合关系,只要根据这一组合关系便可构造新数列,并且求得新数列的通项公式,进而{an}和{bn}解出的通项公式.于是我们不禁要问:这种线性组合又是如何得到呢?事实上,对于
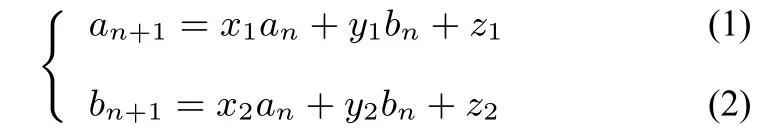
一般都可采用待定系数法进行配凑,引入待定系数λ,由(1)+(2)×λ得an+1+λbn+1=(x1+λx2)an+(y1+λy2)bn+(z1+λz2).其中系数关系满足:从中解得λ的值; 于是就有:an+1+λbn+1=(x1+λx2)(an+λbn)+(z1+λz2).令cn=an+λbn,系数x1+λx2=k,常数z1+λz2=b,则转为cn+1=kcn+b这一常见的线性递推模型来解决!
比如在例4中,对于
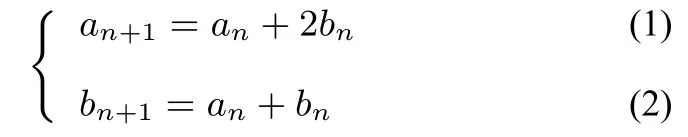
由(1)+(2)×λ得:an+1+λbn+1=(1+λ)an+(2+λ)bn,其中解得这就为我们揭示了这一线性组合中系数的产生本源及新数列构造的来龙去脉!
例5(2008年四川省高中数学竞赛) 已知数列{an}和{bn}满足:a1=1,b1=7,且则
解析对于

由(1)+(2)×λ得:an+1+λbn+1=(-2-4λ)an+(1+3λ)bn其中解得λ=-1或
(Ⅰ) 当λ=-1时,an+1- bn+1=2(an-bn),an -bn=(-6)·2n-1=-3·2n;(ⅠⅠ) 当时,再由解得an=2n+(-1)n,bn=2n+2+(-1)n.故
例6(2000年全国高中数学联赛) 已知数列{an}和{bn}满足:a0=1,b0=0,且n=0,1,2,···.求证:an是完全平方数.
解析对于

由(1)+(2)×λ得:an+1+λbn+1=(7+8λ)an+(6+7λ)bn+(-3-4λ),其中解得



即an是完全平方数.
法二因目标在于{an}的通项,故可将
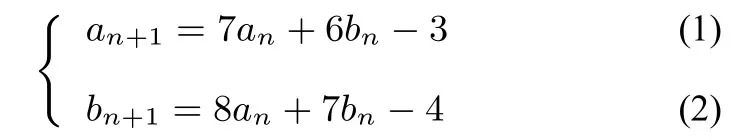
转为{an}的递推关系.
由(1) 得代 入(2) 得:整理得an+2=14an+1-an-6.引入常数λ使得an+2+λan+1=(14+λ)an+1-an-6,其中
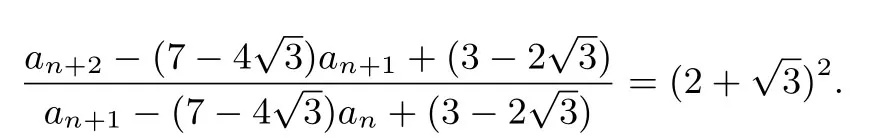
又a0=1,a1=4 可求得

至此我们可发现:对于双数列的递推关系(1)和(2),我们若能配凑出系数λ,即可化成an+1+λbn+1=k(an+λbn)+b的形式,进而构造出以an,bn,的线性组合为对象的新数列(常规数列).然而继续探究还可发现这种递推关系的转换途径并非唯一,我们类似于解二元一次方程组,通过代入消元转为解一元方程.比如将(1) 中“bn”用“an,an+1”表示,代入(2) 中可得“an+2,an+1,an”前后三项的等量关系,然后在此基础上朝着:“pan+2+qan+1=k(pan+1+qan)+b”这一目标模型配凑转化,则也可实现问题的化解!
再如在例5中,由(1) 得bn=an+1+2an,从而bn+1=an+2+2an+1,代入(2) 中可得an+2+2an+1=3(an+1+2an)-4an,即an+2=an+1+2an,假设存在实数k,λ使得:an+2+λan+1=k(an+1+λan),则对照系数可得从中解得或
结束语

这种双数列线性递推问题的实质来源均是常规模型“cn+1=kcn+b(n ∈N*,k0) ”的线性迭代或变式衍生,掌握这一问题本质必然使我们对递推关系的化归转换和配凑构造更具方向性、目的性和创造性,也让我们充分领略到“cn+1=kcn+b”这一经典递推模型的广泛应用性以及化归运算的目标统一性!

