立体几何问题的模型化处理策略——以长(正)方体为例

湖南省衡阳市第八中学

高考中立体几何板块的考查,其中空间中的线线、线面、面面关系及其相关量的计算与证明是主要方向,在高三复习教学中,如何使学生的空间想象能力更上一个台阶,是摆在广大数学教师面前的一大课题.本文试图以长方体和正方体及它们变形出来的模型为例,归纳整理模型化处理策略在立体几何问题的应用,培养学生空间感,寻找解题的突破口,提高解题能力.

问题呈现(2017年高考全国Ⅲ卷第16题)a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:

解析此类问题如果没有具体模型,不太好考虑.发现有三直线两两垂直这一前提条件,可考虑将问题情境放入长方体或正方体中考虑,即构造具体模型求解.

图1

由题意知,a,b,AC三条直线两两相互垂直,画出图形如图1.不妨设图1中所示正方体边长为1,故边AB以直线AC为旋转轴旋转,则A点保持不变,B点的运动轨迹是以C为圆心,1 为半径的圆.以C为坐标原点,以为x轴正方向,为y轴正方向,为z轴正方向建立空间直角坐标系.则D(1,0,0),A(0,0,1),直线a的方向单位向量设B点的起始坐标为(0,1,0),直线b的方向单位向量b=(1,0,0),|b|=1,设点B在运动过程中的坐标B′(cosθ,sinθ,0),其中θ为CB′与CD的夹角,θ ∈[0,2π).

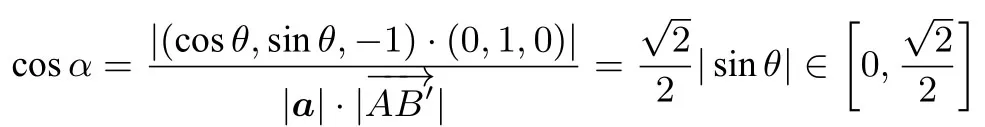
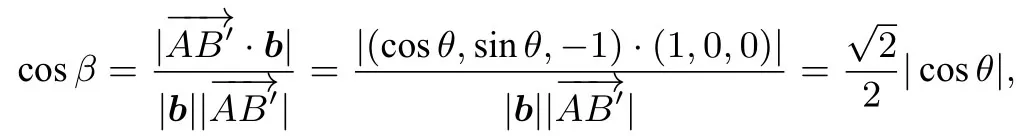
策略一 巧用长(正)方体判断位置关系问题

当问题没有给出具体的图形,只是给出了相关点、线、面的关系(如平行、垂直等),要判断某些元素的位置关系时,通常可考虑构造长方体、正方体模型,把这些线、面变成长方体或正方体中的线段或某一个面,进而加以解决.

例1(2013年新课标Ⅱ卷) 已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥n,l⊥m,l ⊂/ α,l ⊂/ β,则( )

A.α//β且l//αB.α⊥β且l⊥β

C.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l

解析相关的线、面关系条件较多,不妨放入具体模型长方体或正方体中考虑,采用排除、验证等方法求解.如图,长方体ABCD-A1B1C1D1,记平面ADD1为α,平面ABC为β,直线AB为m,直线B1C1为l,直线CC1为n,易排除A,B,C,选D.

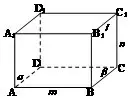
图2

策略二 巧用长(正)方体处理三视图问题

利用长方体、正方体的面为“屏幕”,几何体的正投影可直接在各个面上得到很好的体现,特别是对关于棱锥型的几何体三视图问题,按常规方法不易想象时,不妨运用长方体、正方体模型解决,往往会有“柳暗花明”的效果.

例2一个多面体中某一条棱的正视图,侧视图和俯视

解析初看起来,多面体中某一条棱这一条件让人感觉有点摸不着头脑,若将这个多面体的这条棱嵌入长方体中,如图3,使这条棱为长方体的体对角线BD1,则它在正视图、侧视图、和俯视图中分别对应D1C,C1B,BD,则易求得即为所求值.

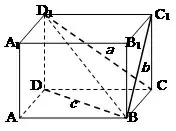
图3

例3(2014年高考全国Ⅰ卷) 如图4,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )

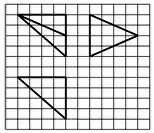
图4

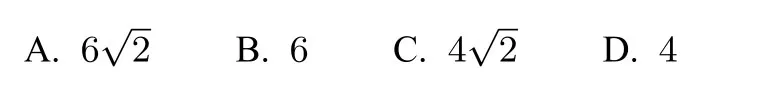
解析由三视图可知,原几何体的长、宽、高均为4,所以我们可用一个正方体作为载体对三视图进行还原.先画出一个正方体,如图(5)(6)(7),画出正视图、侧视图、俯视图的顶点的“原象”,即图中加黑部分的线段,然后找三线交汇处得相应顶点,如图(8),再进行验证,一般可以得出三视图的还原图形,如图(8).

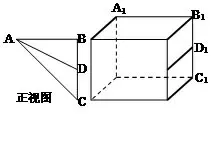
图5

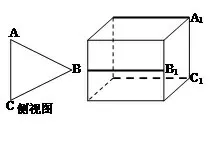
图6

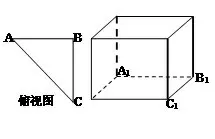
图7

图8

如图(8) 所示,原几何体为三棱锥P - ABC,其中故最长的棱的长度为PA=6,故选B.

策略三 巧用长方体解决多面体与球相接、相切问题

例4(1) 已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是____.

(2) 若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是____.

(3) 在正三棱锥S -ABC中,M,N分别是棱SC,BC的中点,且AM⊥MN,若侧棱则正三棱锥S-ABC外接球的体积是____.

(4) 用6根长度为1的铁棍焊接成一个正四面体框架,若忽略铁棍的粗细,则该框架能够容纳得下的最大球体的半径为____.

解析(1)直接运用长方体模型,由对称性知,球心即为正四棱柱体对角线的中点,如图9所示,由条件可得,底面边长为2,记该球半径为R,所以则S=4πR2=24π.

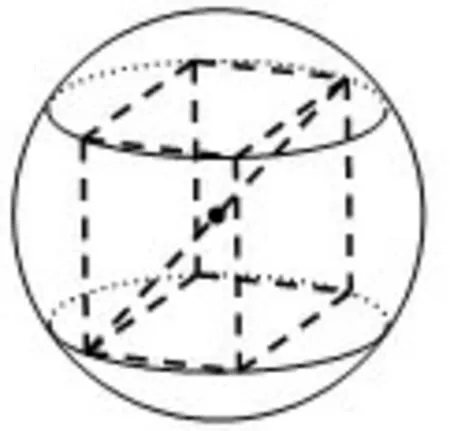
图9

图10

(2) 由条件可知,三棱锥的三条侧棱也两两垂直,且相等.以三条侧棱为邻边构造正方体,如图10所示,于是问题转化为(1) 中类型,所以则S=4πR2=9π.

(3) 由正三棱锥性质知SB⊥AC(对棱互相垂直),又MN⊥AM,所以SB⊥AM,又AM ∩AC=图的长度分别为a,b,c,则这条棱长为.A,可得SB⊥平面SAC,则有SB⊥SA,SB⊥SC,由ΔSAC～= ΔSAB,可知SA⊥SC,以SA,SB,SC为邻边构造正方体,如图11所示,化归成(1) 中类型解决,2R=所以

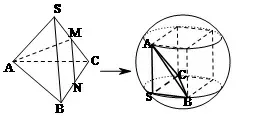
图11

图12

(4) 直接计算有一定的运算量,从整体考虑,可构建正方体模型进行求解.把焊接成的正四面体框架A-BCD放置于其中,如图12所示,则球心为正方体的中心,最大球体的半径为正方体中心到对角线CD中点的距离,另一方面,由CD=1,得正方体的棱长为正方体中心到CD中点的距离为于是最大球体的半径为

评析多面体与球相接、相切问题历年都是高考中的热点,如果能对一些常见的模型加以梳理和归纳,势必能极大地提高解题效率.由例4可看出,多面体中若出现“墙角模型”或“对棱长相等”或“三节棍”模型等(如图13-14),不妨构造长方体或正方体模型求解,能起到事半功倍的效果.

图13

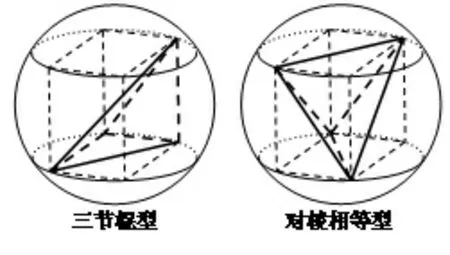
图14

策略四 巧用长方体解决与截面相关的问题

例5正四面体ABCD的棱长为1,棱AB//平面α,则正四面体上的所有点在平面α内的正射影构成的图形面积的取值范围是____.

解析本题中的正四面体ABCD的各棱长都相等,容易联想到正方体,将正四面体ABCD放到正方体中,使正四面体的棱分别是正方体六个面的面对角线(如图16所示),使得所求问题变得非常直观明了.

将正四面体“补成”正方体,正四面体的棱长为1,则对棱互相垂直,且距离为

图15

图16

由于AB// 平面α,所以当CD// 平面α或CD ⊂α.(即将平面AEBF或平面CHDG作为平面α) 时,四面体在α内的射影为正方形,其面积为(最大);当CD⊥α(即将平面ABHG作为平面α) 时,四面体在α内的射影为等腰三角形,其面积为(最小).从而所求面积的取值范围是

策略五 巧用长方体解决空间角计算的问题

例6如图17,在三棱锥A -BCD中,侧面ABD,ACD是全等的直角三角形,AD是公共的斜边,且另一个侧面是正三角形,E是AC上一动点,当ED与面BCD成30°角时,则

图17

解析对于非常规图形,一般会首选空间向量法,但有些时候建系不太容易想,不妨结合题干中的条件,将情境放入长方体或正方体中考虑,会有意想不到的效果.

图18

如图18,正方体棱长为1,过E作EF⊥CG于F,连ED,则∠EDF即为ED与平面BCD所成的角,即∠EDF=30°,设CF=x,则在RTΔEFD中,可得此时