融合知识图谱和协同过滤的学生成绩预测方法

陈 曦，梅 广，张金金，许维胜，3*

（1.同济大学电子与信息工程学院，上海201804；2.同济大学教育技术与计算中心，上海200092；3.同济大学信息化办公室，上海200092）

0 引言

学生成绩预测是教育数据挖掘（Educational Data Mining，EDM）领域的研究热点之一。研究通过对课程设置、学生历史成绩或其他背景数据的分析，预测学生在未来学习阶段的表现。高等教育中日益严重的退学问题使采用更为创新有效的方法促进学生及时毕业已成为迫切需求：文献［1］分析了全美的教育数据，发现在所有2011 年秋季入学攻读四年制学士学位的学生中，仅有60%在6 年内完成了学业。众多教育家认为早期成绩预测是解决该困境的一种实用的方法：文献［2-4］都曾通过一系列实验表明早期识别出有退学风险的学生是防止他们辍学的一个关键举措。

随着数据挖掘技术在教育领域的兴起，大量数据挖掘的方法被应用于学生成绩预测的研究中。现有的研究方法可分为两类：一类是将预测问题视为回归或分类问题，应用线性回归［5］、决策树［6-7］、支持向量机［8］、深度神经网络［9］、贝叶斯网络［10］等数据挖掘模型。另一类是将学生预测问题类比成推荐系统中的用户评价问题，借用推荐领域的技术解决问题，包括协同过滤（Collaborative Filtering，CF）、矩阵分解（Matrix Factorization，MF）等方法［11-17］。与基于回归的方法相比，基于推荐的方法因为其较高的预测精度和可解释性得到更为广泛的应用。

但是，基于推荐的方法往往在缺乏历史数据的情况下性能较差。该类方法主要依赖学生成绩的历史记录挖掘课程的相似性，进而对结果进行预测，因此在课程的历史选课人数较少时，必须采用额外的信息帮助准确刻画课程之间的相似度。例如学生的知识基础和课程的知识领域，这两者之间的重合度与课程成绩息息相关，如果能够揭示出这种关联，并运用到成绩预测中，预测的精度将有机会得到改善。但在学生成绩预测领域，大多数研究都只利用了与知识信息关联较弱的学生背景信息或课程背景信息，包括学生年级、课程难度、课程学时等。这些背景信息通常类别冗杂，对数据源的要求较高，且对知识信息的挖掘有限。目前为止，还未见依赖知识信息预测学生成绩的研究。

本文研究如何利用课程知识信息对高等教育中本科生在本科学位课程上所取得的成绩进行预测。研究通过TextRank算法［18］从课程信息中提取关键字作为知识点，再结合数据库中其他课程信息，构建了基于课程信息的知识图谱Knowledge Graph，KG)来表示课程的知识信息。在知识图谱的 帮 助 下，本 文 借 助 节 点 亲 密 度 算 法（Adamic Adar［19］，Preferential attachment［20］，Resource Allocation［21］）和知识图谱表示学习算法（Translating Embeddings［22］和DistMult Model［23］）挖掘课程之间的知识相关性，并比较了它们在传统CF框架下的有效性。

本文的主要工作如下：

1）基于同济大学2013—2017 年间的本科生课程信息构建了课程知识图谱。

2）提出了一种在CF 框架下利用课程知识信息进行成绩预测的方法，并利用同济大学的本科生成绩数据验证了方法的有效性。

1 研究现状

现有研究表明了基于推荐的算法在成绩预测领域的有效性和利用课程信息建立教育类知识图谱的可行性，为从知识层面发掘课程关系并应用于预测学生成绩提供了理论基础。

1.1 基于推荐算法的成绩预测方法

学生成绩预测问题常与推荐系统中的用户评价问题进行类比，现有的研究也将推荐领域中的相关技术用于预测学生的成绩。文献［11-12］使用CF 方法预测成绩并证明了CF 在学生成绩预测上的表现优于传统回归方法。文献［13］以CF为底层算法构建了一个选修课推荐系统并应用在中山大学。该应用使得选修课程的退课率大幅下降，进一步证明了CF的有效性。文献［14］扩展了传统的推荐算法，利用学生的历史成绩以及乔治梅森大学的各种课程背景资料和学生资料解决成绩预测问题；研究提出了一种混合分解机和随机森林（Factorization Machine with Random Forest，FM-RF）的方法用于准确预测学生在课堂上的表现。文献［15］在CF 框架下开发了三种融合了时间信息的预测方法，并对明尼苏达大学的学生成绩数据进行了一系列实验，验证了方法的有效性。

上述成绩预测方法大多忽略了学生成绩随着学生努力程度而改变的事实基础。为解决上述问题，一些研究者基于学生的学习过程对成绩的影响提出了动态预测算法：文献［16］使用历史成绩信息和可用的附加信息（如期中考试成绩）来预测学生未来课程的成绩，研究采用MF 方法并得到了较好的结果；文献［17］在评估学生行为的基础上，提出了一种基于MF的动态预测学生学习成绩的方法。

1.2 教育知识图谱的构建和应用

在教育领域，知识图谱也称概念图［24］或领域模型［25］，主要关注包括课程和知识在内的教育实体及其之间的连接关系。挖掘每门课程的关键知识是构建课程知识图谱的过程中必不可少的一步。挖掘关键知识的一类方法是使用关键字提取 算 法，包 括TextRank［18］和TF-IDF（Term Frequency-Inverse Document Frequency）［26］。该类方法将课程信息视为普通文献，提取其中的关键字作为关键知识，文献［27］就使用关键字提取方法基于MOOC课程信息构建了课程知识图谱。另一种方法是利用实体链接技术识别知识点。例如：文献［28］利用教学数据和实体识别技术，从MOOC 平台的课程信息中提取了教学概念；文献［29］提出了一种利用Web 知识从数字图书中提取概念层次结构的方法，并通过该方法将图书内部的知识与外部的知识资源连接起来；文献［25］提出了一种从电子教材中半自动生成知识模块的框架DOM-Sortze。

知识图谱特殊的结构为计算节点的相似度提供了可能性。将知识图谱看作由节点和边组成的网络结构，可以使用一些链路预测方法来计算节点间的紧密度，包括Adamic Adar［19］、Preferential attachment［20］以及Resource Allocation［21］。一些知识图谱表示学习算法也可以用于计算每个节点的特征向量，从而计算节点相似度，如TransE（Translating Embeddings）［22］、DistMult［23］和ComplEx［30］。

2 课程知识图谱的构建

本章设计了课程知识图谱的结构，并使用TextRank［18］对知识图谱进行实体提取，以完成图谱的构建。

2.1 知识图谱结构

本文研究使用同济大学的课程信息相关数据构建课程知识图谱。通过对数据的分析，本文选取了以下实体：“院系”“课程”“知识点”“教材”“参考书”和“教学模式”。“院系”实体指开设该课程的机构；“知识点”实体指学生在完成课程后应该掌握的概念或技能；“教学模式”实体指教学过程中所采用的教学方法，如讲课、讨论或实践。图1 描述了几个实体之间的关系类型：图中节点代表实体，边缘代表实体之间的关系。图2 展示了部分知识图谱；图谱以“模式识别”“模式信息处理”及“模式识别及其地学应用”这三门课程为中心发散，展现了三门课程之间的联系。其中圆形节点表示“课程”实体；白色矩形节点表示“知识点”实体；灰色矩形节点表示“院系”实体；实线箭头表示“院系-OFFER-课程”关系；虚线箭头表示“课程-COVER-知识点”关系。可以看出，知识图谱可以直观地反映课程的相关特征以及不同课程之间的联系。

2.2 课程知识相关性挖掘

课程知识图谱中涉及的大部分实体和关系可以从数据库中获取。而“知识点”实体需要从课程简介中提取。课程简介的文本往往结构统一，大都包含相似的词汇和句型。除去通用词汇，课程简介主要由专业术语组成。综上，利用简单的关键字提取方法即可提课程简介中所包含的关键知识点。本节使用TextRank从中提取“知识点”。

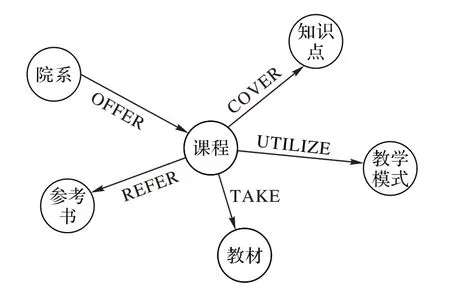
图1 课程知识图谱的结构Fig.1 Structure of course knowledge graph

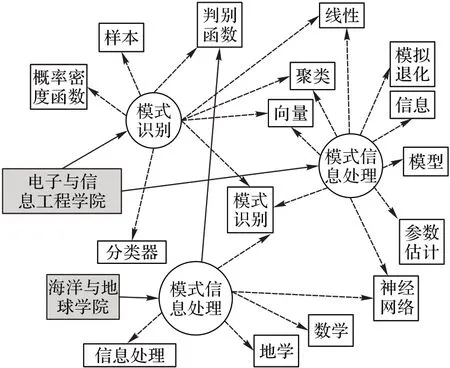
图2 知识图谱示例Fig.2 Sample of knowledge graph

TextRank 的主要思想是建立基于词之间邻接网络，并使用PageRank［31］计算每个节点的Rank。算法选择Rank 数值较大的单词作为关键词。首先将给定的课程简介文档D分成完整的句子[S1，S2，…，Si]；对句子Si进行分词和词性标注。分割后从句子中过滤停止词，留下带有指定词性的单词。停止词包含一些常见但无意义的词，如“学时”“课堂”“理论”和“大学”。根据上述规则将Si分成一组单词[ti，1，ti，2，…，ti，n]，其中，ti，n表示句子中的第n 个候选单词。算法根据这些单词构建候选关键字网络G=(V，E)，每个候选单词ti，n对应一个节点，V 是所有节点的集合；E 则是由代表节点之间共现关系的边组成的集合。共现关系是指一对节点对应的两个词在长度为K 的文本窗口内共现。在本文中，K 设置为30。根据式（1）迭代计算各节点的Rank(Vi)直到收敛，再选择Rank(Vi)的数值较大者作为关键词。

其中：d 为用于平滑的参数；In(Vi)是Vi的前继节点，Out(Vj)为Vj的后继节点。

TextRank 虽然可以有效地从课程简介中提取关键字，但无法识别知识点间的歧义现象。例如，“神经网络”一词在“模式识别”和“人体解剖学”两门课程中就有不同的含义。由于该词汇在这两篇文档中具有相同的词性和所处语境的相似性，很难将其区分开来。

一个术语的意义取决于它的领域；在本文中，这体现在课程所处“院系”和课程包含的“知识点”这两个实体上；即“模式识别”课程由“电子与信息工程学院”开设，“人体解剖学”课程由“医学院”开设，且这两门课程涵盖的“知识点”存在显著差异。对含有相同关键词的课程，比较其所属院系和包含的“知识点”。如果这两门课程来自不同的院系或超过一半的“知识点”是不同的，即认为两门课程不属于同一知识领域，可能在同一个关键词上有不同的含义。考虑到数据库中存在大量的交叉学科课程，本文在上述歧义检测的基础上进行人工确认，从而确保消歧过程的准确性。

3 成绩预测方法

基于已构建的课程知识图谱，分别采用基于邻节点的方法和基于知识图谱表示学习的方法从知识图谱中挖掘课程相似度，该相似度揭露了课程在知识领域的关系。在缺乏历史数据的场景下，课程在知识层面的关联为CF框架提供了相似度的计算途径；知识相似度与基于历史纪录的相似度之间互为补充，使得预测结果更接近真实数据。

3.1 算法框架

算法首先生成课程相似度矩阵，再选取k 个与目标课程相似度最大的课程作为相似课程。学生在相似课程上分数的加权平均值即为学生在目标课程获得的分数。当预测学生s在课程c 上所取得的成绩时，根据课程知识图谱计算c 和s 上过的历史课程[c1，c2，…，ci]的知识相似度。基于知识相似度筛选出相似度高的k个课程。s在这k门课程上所得成绩的加权平均即为目标课程c的成绩估计est1，计算加权平均值时以知识相似度为权重。本文也使用基于历史记录的传统CF 生成估计值est2。对这两种预测模型作线性集成，得到最终预测ScoreEst。图3给出了算法流程。

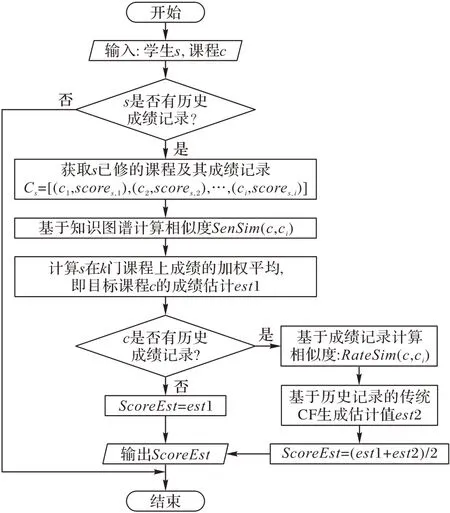
图3 预测算法流程Fig.3 Flowchart of prediction algorithm

3.2 相似度计算

3.2.1 基于邻节点的相似度计算

基于邻节点的相似度计算方法将知识图谱看作由节点和边构成的网络，用课程对应节点之间的亲密度衡量课程相似度。本节采用了多种基于邻节点的节点亲密度算法来计算课程间的知识相似度，并按照3.1节所述与CF框架融合。

在基于邻节点的方法中，邻节点的数量对于确定一对节点的相似性起着至关重要的作用。两个节点共享的邻节点越多，关系就越亲密。本文使用了一些经过链路预测领域验证的节点亲密度计算方法，包括Adamic Adar［19］、共享邻节点数量（Common Neighbors）、Preferential Attachment［20］、Resource Allocation［21］、同属社区（Same Community）和邻节点总数量（Total Neighbors）。具体的计算公式如（2）～（6）所示。

对于Adamic Adar：

其中：N(u)表示u的邻节点，| |

N(u)表示N(u)的节点数量。

对于Common Neighbors：

对于Preferential Attachment：

对于Resource Allocation：

Same Community是通过确定两个节点是否属于同一社区来决定两节点关系的一种方法。该算法将网络划分为不同的社区，值为0 表示两个节点不在同一个社区中，值为1 表示同属一个社区。本文定义课程知识图谱中同一个连通域内的点属于同一个社区。

利用上述公式计算课程所对应节点的亲密度，并将其作为课程之间的相似度应用于后续计算中。

3.2.2 基于图谱表示学习的相似度计算

知识图谱的表示学习是一种将知识图谱的实体和关系转化为低维向量的方法。为了将实体和关系嵌入到低维向量空间中，使用三元组的集合表示知识图谱。以本文为例，课程知识图谱G 可以看作三元组(sub，pred，obj)的集合，每个三元组包含一个主体sub ∈Entity，一个谓词pred ∈Relation，以及一个对象obj ∈Entity。Entity 和Relation 分别是所有实体和关系类型的集合。例如，“课程”实体C 以及“院系”实体D 连接形成一个三元组：(D，offer，C)。推断三元组中的一对节点在知识图谱的语义上是相似的。有效的知识图谱表示形式应该能够将图谱中存在的三元组（正三元组）和不存在的三元组（负三元组）区分开，即正三元组中，实体所对应的嵌入向量相似，负三元组中，实体所对应的嵌入向量差异大。本文采用了TransE［22］和DistMult［23］对图谱进行低维嵌入。得到嵌入向量之后，使用Pearson 距离来度量向量之间的相似度，从而得到课程之间的相似矩阵。

TransE 和Distmult 使用评分函数S(t)对正三元组t+和负三元组t-评分；再通过合适的损失函数尽可能地让负三元组的得分显著低于正三元组。

本文中，TransE的评分函数采用L2范数：

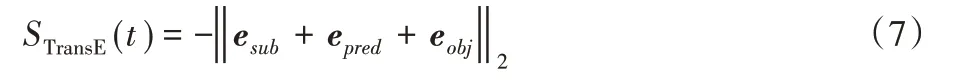
对于Total Neighbors：

其中，esub、epred、eobj分别表示sub、pred、obj的嵌入向量。

DistMult模型采用三线性点积作为评分函数：

本文中采用了pairwise 损失函数和negative log-likelihood损失函数训练TransE和DistMult，计算公式如（9）和（10）。

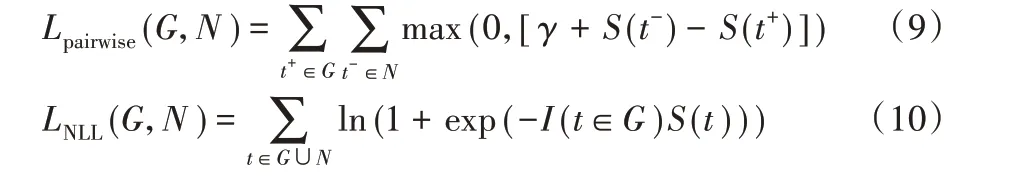
其中：γ为边缘参数，表示正负三元组的区分度；G是正三元组的集合，N 是负三元组的集合，由替换正三元组的sub 或obj而生成；I()是指示函数，I(t ∈G)在t ∈G的时候取1，其余为0。

使用上述方法计算得到的k 维向量表示课程，并生成相似度矩阵。

相对于基于邻节点的方法，基于知识图谱表示学习的方法考虑了不同关系具有的不同意义。例如，来自同一“院系”的课程比只有一个共同“知识点”的课程在知识层面上更相似。但在以邻节点为核心的方法中，相似度只与共同邻节点的数量相关。

4 实验与讨论

为验证学生知识基础和课程知识信息在学生成绩预测中的有效性，本文进行了一系列对比实验来衡量提出的预测算法在不同场景下的预测精度，实验场景包括冷启动问题、数据稀疏场景和数据密集场景。

4.1 实验设置

4.1.1 数据集

实验中采用的数据集是来自同济大学的1 217 086 条课程成绩记录。数据集涉及23 903名本科生和5 378门课程，涵盖了2013 年至2017 年所有在校本科生的课程记录。每一项成绩记录描述了学生、课程以及相应的课程成绩（5 分制）。图4描绘了课程数量关于选课人数的分布；图5则是学生数量关于选课数量的分布情况。

如图4 所示，大部分的课程选课人数在［10，500）区间。仅有11.64%的课程选课人数少于10人，即11.64%的课程会出现数据稀疏或冷启动问题。使用传统CF 对这部分课程进行成绩预测的效果有限。

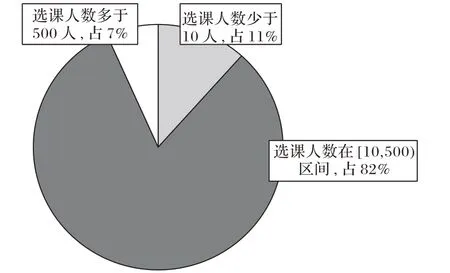
图4 课程数量关于选课人数的分布Fig.4 Distribution of number of courses corresponding to number of students

从图5的数据可以得出，95.14%的学生的选课数量在10到100 之间，数据表明大部分学生拥有足够的成绩记录来保证预测的准确性。只有0.41%的学生选课门数少于10门，这些学生多是交流生或联合培养项目参与者，他们的成绩计算方法及成绩记录仍保留在原学校，因此不属于本文研究的探究范畴。

在实验过程中，按照3∶1 的比例将数据集划分为已知成绩数据集和测试数据集。实验将记录每一种算法在已知部分成绩数据的基础上预测成绩的误差。

图5 学生人数关于选课门数的分布Fig.4 Distribution of number of students correspongding to number of taken courses

4.1.2 课程知识图谱

本文构建的课程知识图谱组成如表1、2所示。

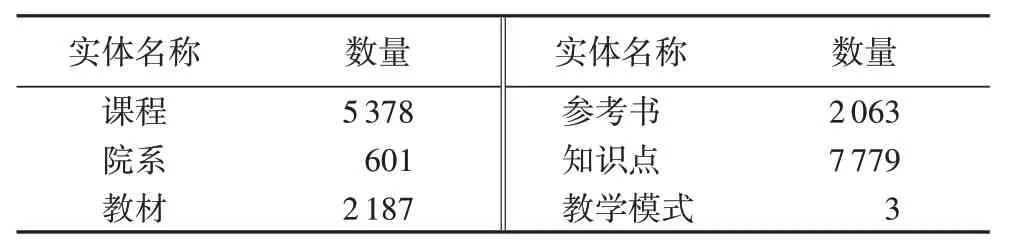
表1 实体类型及其数量Tab.1 Types and numbers of entities

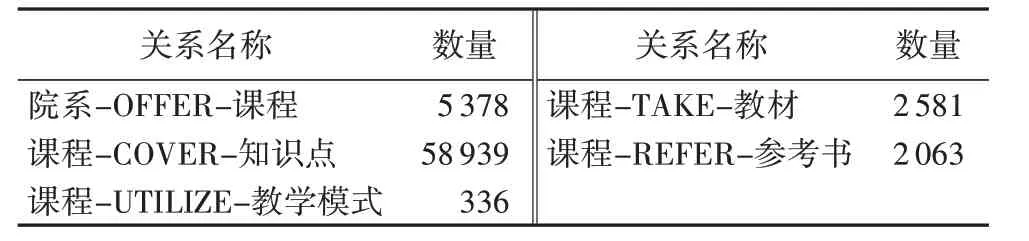
表2 关系类型及其数量Tab.2 Types and numbers of relationships

课程知识图谱共有69 297个三元组，选取其中的2 000个作为训练嵌入向量模型的测试集，并通过嵌入向量模型在测试集上的表现评价生成的嵌入向量。

4.1.3 评价指标

实验采用均方根误差（Root Mean Square Error，RMSE）和平均绝对误差（Mean Absolute Error，MAE）两个指标对预测结果进行了评估，计算公式如式（11）、（12）。

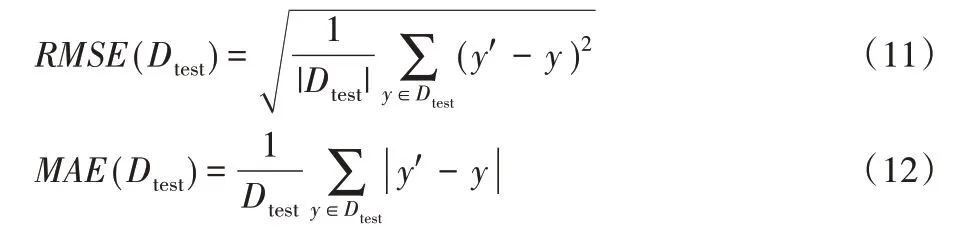
其中：Dtest表示测试集；y'和y 分别表示样本的预测结果和该样本的实际得分。

本文使用平均互反排名（Mean Reciprocal Rank，MRR）和Hit@10 评价嵌入向量的准确性。对于测试集中的每个正三元组，实验通过替换它的主体或对象来生成一系列的负三元组。模型使用得分函数计算这些正负三元组的得分并按得分降序排列三元组；其中正三元组在其生成的一系列负三元组中排名为rank(s+，p，o+)。Hit@10是指排在前10位的正三元组的比例。MRR则按照式（13）计算。

其中Gtest表示测试三元组的集合。

MRR和Hit@10的数值越大，说明测试集中排名靠前的正三元组数量越多，即嵌入向量对知识图谱的描述能力越强。

4.1.4 基准

实验采用三种常用成绩预测算法在数据集上的实验结果作为基准。一是基于正态分布的成绩预测方法（Normal Prediction），该方法将所有学生在某一门课程上获得的成绩视为正态分布，通过随机取样获得待预测成绩；二是基于奇异值分解（Singular Value Decomposition，SVD）的矩阵分解方法［32］。三是基于项目的协同过滤（Item-Based CF）方法，该方法采用Pearson距离来衡量课程之间的相似性，并选取学生在40个相似课程上的成绩加权平均值作为预测值。实验通过对比每种预测方法得出的实验结果与三种基准算法中的最优结果，检验知识图谱对预测算法的优化程度。

4.2 基于邻节点的方法

实验融合了传统CF和基于邻节点的相似度，并从整个数据集中选取了3 段具有代表性的数据来检验邻节点法的有效性：1）选课人数少于10 人的课程；2）选课人数在［10，500）区间的课程；3）选课人数大于500人的课程。场景1的课程选课人数较少，冷启动问题和数据稀疏问题较严重；场景2 几乎不存在冷启动问题，数据稀疏问题有所减轻；场景3 为数据密集场景。表3记录了算法在数据稀疏性不同的场景下的性能。

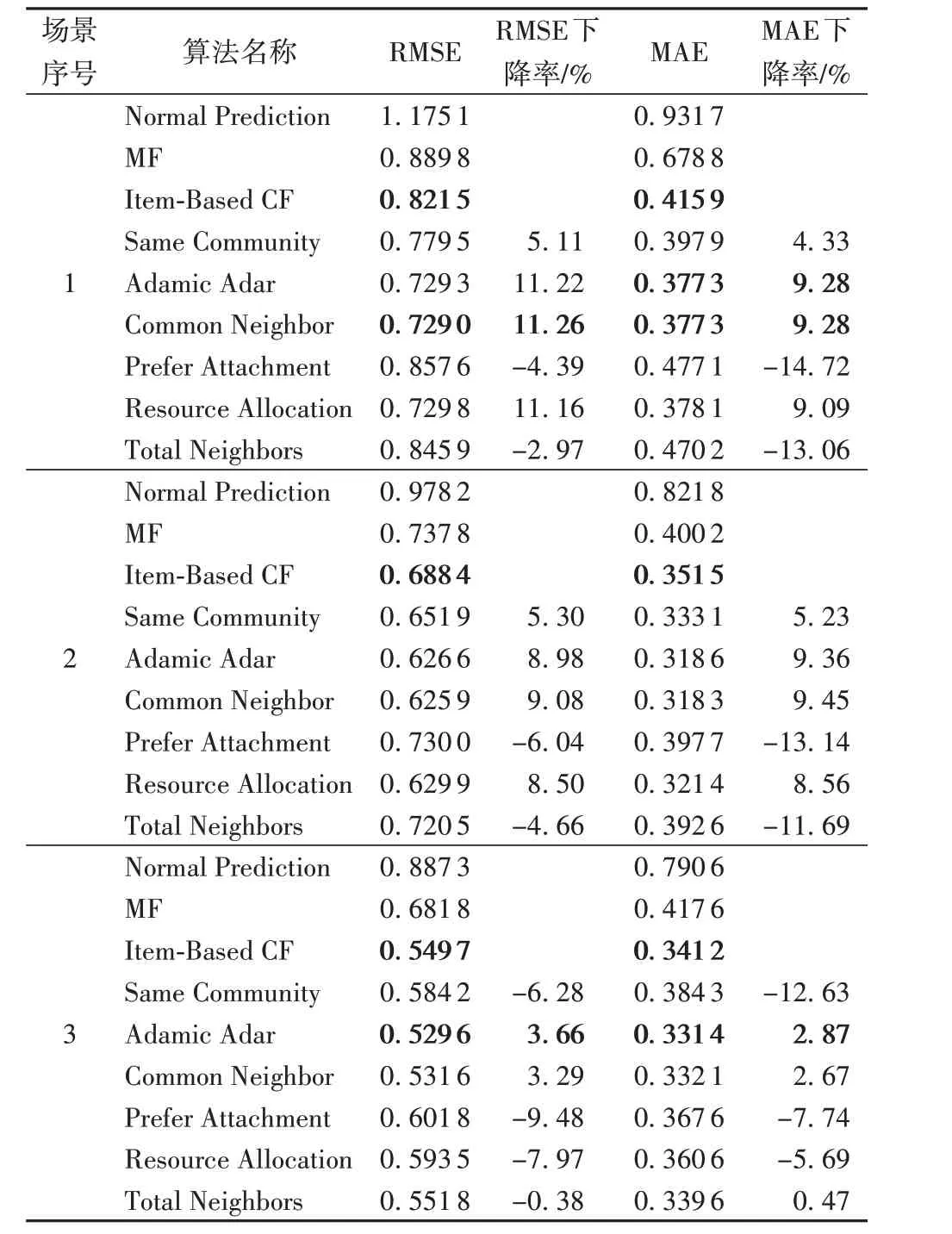
表3 基于邻节点的算法多场景下的性能Tab.3 Performance of neighbor-based algorithms in multiple scenarios

从实验结果可得，在冷启动和数据稀疏的场景下，基于邻节点的方法显著降低了预测误差。表3中场景1数据显示，在数 据 稀 疏 场 景 下，Resource Allocation、Adamic Adar 和Common Neighbor 与结果最优的基准算法相比都在RMSE 指标上下降了超过10%，在MAE 指标上下降约9%。此外，场景2和场景3的数据表明，知识图谱在选课人数较多的情况下仍对预测结果有改善。对于选课人数在［10，500）区间的课程，与Item-based CF 方法相比，基于邻节点的方法使RMSE 和MAE 分别下降了9%；对于选课人数大于500 人的课程，性能最优的算法Adamic Adar 与Item-Based CF 方法相比，其RMSE下降了3.66%，MAE 下降了2.87%。综合表3 的数据，可以发现传统CF的性能随着历史数据的丰富而逐渐变好，而知识图谱的作用随着数据稀疏程度的减弱而减弱。

4.3 基于图谱表示学习的方法

本节在传统CF 中融合通过TransE 和DistMult 计算的相似度。实验首先利用课程知识图谱生成嵌入向量，并用MRR和Hit@10对嵌入向量进行评价。经过训练和验证，设置嵌入向量的维度为200；本文使用Pairwise 损失函数训练TransE，使用negative log-likelihood 损失函数训练DistMult。表4 给出了两种嵌入向量的详细评价。

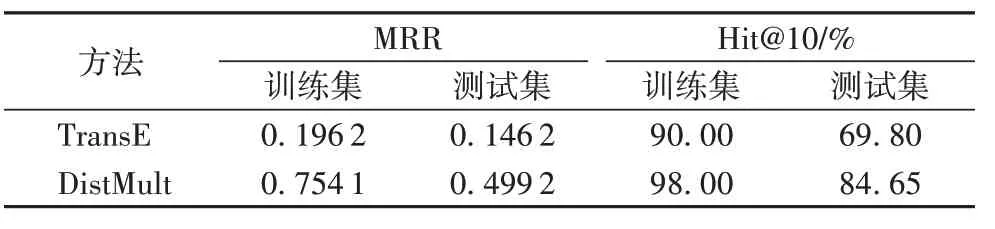
表4 TransE和DistMult的评价Tab.4 Evaluation of TransE and DistMult

利用Pearson 距离计算嵌入向量的相似性。为了验证基于知识图谱表示学习的方法的有效性，从整个数据集中选取与4.2节同样的三段数据进行实验，结果如表5所示。

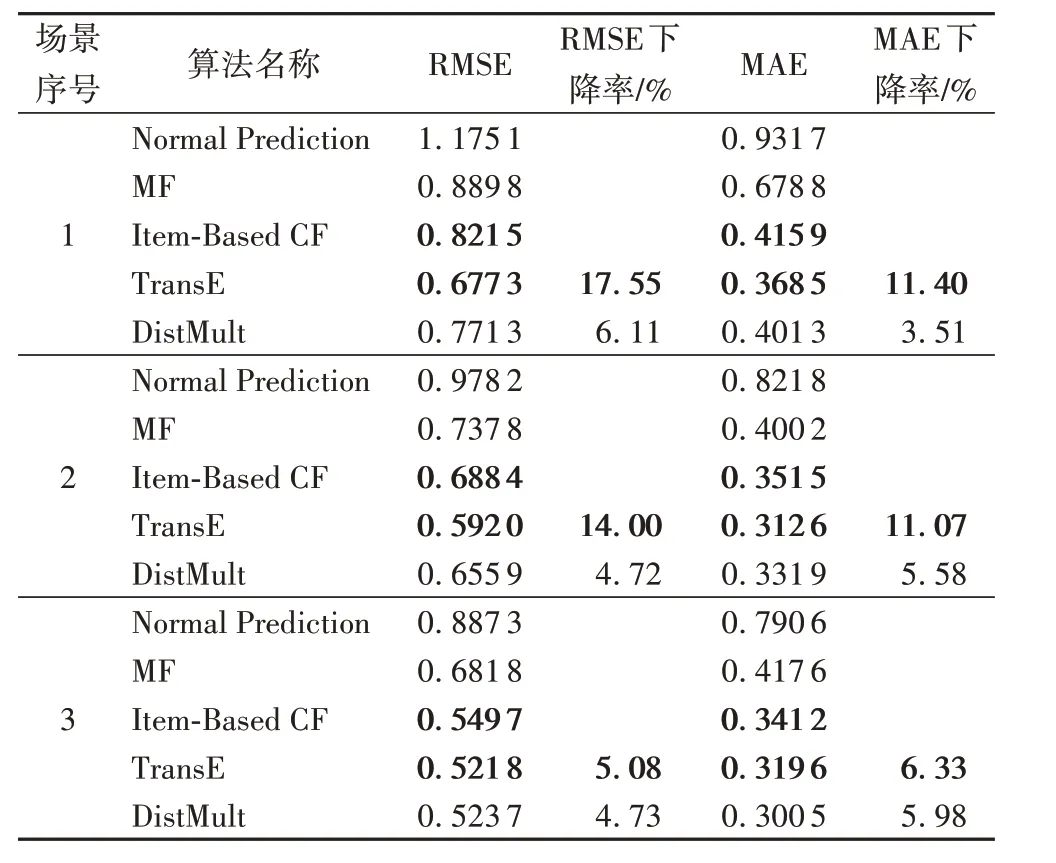
表5 基于图谱表示学习的算法在多场景下的性能Tab.5 Performance of KG representation-based algorithms in multiple scenarios

表5 说明了基于图谱表示学习的方法对传统CF 的预测结果有显著的改善。场景1）数据显示在数据稀疏场景中，性能最优的算法与Item-Based CF 相比在RMSE 和MAE 指标上分别下降了17.55%和11.40%。随着数据的丰富，基于图谱表示学习的方法相比于传统CF依然有优势，且在各个场景下的预测性能都优于基于邻节点的方法。比较TransE 和DistMult，尽管DistMult 在描述知识图谱（包括MRR 和Hit@10）方面的性能优于TransE，但TransE在上述几种情况下的表现都优于DistMult。

4.4 结果分析

本文研究结果表明，知识图谱可以帮助传统CF实现更准确的学生成绩预测。在冷启动和稀疏数据的情况下，基于邻节点的方法和基于图谱表示学习的方法均使RMSE 和MAE显著下降。实验结果显示，使用Adamic Adar、Common Neighbors、Resource Allocation、Same Community、Total Neighbors、TransE 和DistMult 等算法计算的知识相似性有助于预测结果的改善。这种改善可以归因于知识图谱提供的语义信息。传统CF往往通过历史数据评估相似度，不同课程之间对学生能力要求的共性和学科之间思维模式的相通性确保了传统CF能够有效地刻画课程间的联系，从而取得不错的预测效果。但在历史记录缺乏的场景下，小数据量不足以支持CF 准确地刻画课程间的关系。而利用课程知识信息构建的知识图谱可以作为相似度计算的另一种途径；知识图谱更偏重于从教学内容挖掘课程之间的关系，它刻画了不同课程在知识领域上的交集；从学生的先验知识和课程的教学内容出发，提供预测结果。

实验结果还表明，随着数据稀疏程度的减弱，知识图谱对预测精度的改善逐渐减弱。对此可能的解释是信息的冗余。以往的文献都证明了CF 在历史评分数据充足的场景下可以有效发掘课程之间的关联，这种关联既包括学科之间逻辑思维层面的相通性，又涵盖了知识层面的共同性。在历史数据不足的情况下，知识图谱提供的信息揭露了课程在知识层面的交叉，从而有助于表示课程关系，帮助CF 框架更好地预测成绩。在密集数据情况下，知识图谱所包含的信息和历史数据本身发生冗余；因此，在历史数据密集的场景下，知识图谱对预测性能的提升有限。

5 结语

本文研究通过结合关键字提取算法和消歧方法构建了一个课程知识图谱模型；并从图谱结构和语义信息两个角度出发，分别使用基于邻节点的方法和基于图谱表示学习的方法发掘了课程在知识层面的关系；本文随后对其在学生成绩预测中的应用进行了探讨。实验结果表明，知识图谱可以从知识领域的层面有效计算课程相关度；对传统CF在历史记录基础上得出的课程关联作了信息补充，对课程关联作了更加完善的刻画，从而得到了比传统CF更好的预测性能。

本文探索了知识图谱在学生成绩预测中的应用，并验证了其可行性和有效性。与传统的成绩预测研究相比，本文提出的方法融合了学生的知识基础和课程的教学内容，为后续解读预测结果提供了更多角度。

然而在本文研究中，知识图谱的结构不够细化，限制了语义信息进一步的挖掘。例如，本文提出的“知识点”实体可以分为几个子类型，如技能、概念、公式和理论。更详细的知识图谱将会暴露更多的语义信息。后续将对知识图谱的结构作进一步的优化。此外，本文研究只是将知识图谱与CF框架进行了简单的整合，未来的研究可以考虑将知识图谱应用于更多的推荐算法框架，进一步优化预测性能。