面向期限感知分布式矩阵相乘的高效存储方案

赵永柱，黎卫东，唐 斌，梅 峰，卢文达

（1.国网陕西省电力公司信息通信公司，西安710065；2.计算机软件新技术国家重点实验室（南京大学），南京210023；3.国网浙江省电力有限公司，杭州310007）

0 引言

随着互联网、云计算、物联网的迅猛发展，无处不在的移动设备、传感器持续产生数据，数以亿计用户的互联网服务时时刻刻产生巨量的交互，使得数据呈现出爆炸式增长趋势。大规模的数据资源为大规模的机器学习和数据挖掘应用提供了物质基础，因此近年来涌现了很多大规模的机器学习模型。这些模型在语音处理、图像处理、自然语言处理、人机对弈等领域表现出非凡的问题处理能力；但是大规模机器学习的训练对计算能力和存储容量都提出了较高的要求，单机训练和存储开销太高，利用分布式计算技术来完成训练任务已成常态。

矩阵-向量相乘，简称矩阵相乘，即计算y=Ax（其中，A为矩阵，x 为向量），是很多数值计算、机器学习算法中的核心计算，比如求解偏微分方程［1］、神经网络的前向后向推进［2］、计算PageRank［3］等。通过多台机器来分布式计算矩阵相乘时，通常将矩阵A 进行分割后分配到系统中的各个工作节点（worker node），每个节点将子矩阵与x进行相乘后将结果交回给主节点（master node），由主节点整合出最终的计算结果。在这种方式下，主节点需要等到所有工作节点均返回计算结果后方可完成整体计算任务。

然而，大规模分布式系统由于资源竞争、负载均衡、网络变化等诸多原因，工作节点在执行计算任务时，其完成时间经常难以预测且表现出较大波动，从而会有部分计算节点计算严重滞缓，其计算完成时间能超出平均水平5～10 倍，从而严重拖累整体计算。这样的节点通常被称为落后节点（straggler），产生的问题被称为落后者问题［4-5］。

近年来，研究者提出采用编码的方法能够有效应对上述落后者问题。Lee 等首先提出基于MDS（Maximum Distance Separable）码的编码方案［6-7］，即将矩阵划分成k 份，并应用码率为k/n的MDS码，将其编码成n份（n为工作节点个数），每个工作节点存储其中一份并完成计算。这种方法可以容忍nk 个落后节点。这种方法将落后节点等价于传统通信中的擦除（erasure），无法利用落后节点上的部分计算结果，从而导致性能欠佳。为了能够利用落后节点，研究者从不同的角度提出了一些可行方案［7-10］。其中，Mallick 等提出了基于喷泉码的编码方案［10-12］，利用喷泉码的无码率特性，可以将k 份子矩阵编码成任意多的编码子矩阵，并将这些编码子矩阵预先存储到工作节点上去，而工作节点则可以逐步计算并返回每个编码子矩阵与向量x 相乘的结果；与此同时，主节点只需要接收到的部分计算结果数略多于k 即可恢复出完整计算结果。与其他方法相比，这种基于喷泉码的方式能够充分利用每个工作节点的计算能力，且具有线性的编译码复杂度。

Mallick 等的工作假设每个工作节点存储的分片数充分多，从而保障在整体计算完成前，每个工作节点均持续进行计算［10］，但这种方式将消耗过多的存储资源，从而导致计算成本过高。譬如，用户以租用云计算平台的方式进行分布式计算，成本开销与存储开销密切相关。另一方面，如果工作节点存储的编码子矩阵数目过小，则可能导致工作节点因过早完成分配给它的计算任务而处于空闲状态，从而延长整体计算完成时间。因此，存储开销与整体计算完成时间存在一定的权衡关系。

基于上述分析，本文首先对如何在保障给定期限内大概率完成计算任务的前提下优化工作节点的存储开销问题进行了建模。该问题求解面临的难点有两方面：一是工作节点的耗时具有随机性；二是工作节点的异构性，即其耗时相关的参数不同。通过理论分析发现，在通常情况下，一定时间内主节点接收到的计算结果个数以较大概率集中在其期望值左右，从而提出了基于期望近似的解决思路，将原问题约束条件进行了转化。由于转化后的问题仍是整数规划问题，进一步地考虑了松弛，并证明松弛后的优化问题为凸优化问题，从而可以高效求解，并将其最优解通过简单的取整转化为未松弛问题的可行解。仿真实验结果表明，所提方法能够在保障整体计算在期限内大概率完成的前提下，大幅度降低总体的额外存储开销。

1 问题建模

1.1 系统模型

考虑在一典型分布式计算环境中计算y=Ax，其中，A ∈ℝr×m是大小为r×m 的矩阵，x ∈ℝm为m 维的向量。该计算环境由一个主节点（master node）及n 个工作节点构成。考虑采用喷泉码的方法有效应对落后者问题。具体而言，如图1 所示，首先将矩阵A 按行分割成k 个大小相同的子矩阵(a1，a2，⋅⋅⋅，ak)（如果r 不能被k 整除，可以通过补0 完成），每个子矩阵包含r/k 行，并利用喷泉码（如LT 码［13］、Raptor 码［14］）对这k 个子矩阵进行编码，可以生成一系列（数量可以无穷多）的编码子矩阵，其大小与这k个子矩阵保持一致。

图1 矩阵预编码和部署Fig.1 Matrix pre-coding and allocation

令ci为第i个工作节点放置的编码子矩阵个数，并记这些编码子矩阵为，则第i 个工作节点按序计算，每算完一个就将结果发送给主节点。当主节点从所有工作节点处接收到(1+ε)k 个这样的结果时，可以通过喷泉码的Peeling 算法［10］进行解码，从而能够以非常接近1 的概率恢复出(a1x，a2x，…，akx)，其中ε ＞0 是一个非常小的常数，称之为解码条件。整个工作流程如图2所示。

图2 编码矩阵相乘的流程Fig.2 Flowchart of coded matrix multiplication

1.2 耗时模型

为刻画任务完成时间，本文采用与文献［10］相同的耗时模型。每个工作节点i 的耗时包含两部分：一是启动时延Xi，它服从参数为μi的指数分布，即Xi～exp(μi)；二是每计算并返回一个结果给主节点所需要的时间为常数τi。因此，工作节点返回Ri个计算结果所花费的时间为：

其中Ri＜ci。此外，Xi之间是独立的。本文考虑了工作节点之间的异构性，即对于不同的i，μi和τi的取值可能不同，如图3所示。

图3 耗时模型与任务执行示意图Fig.3 Schematic diagram of time consumption model and task execution

1.3 期限感知的存储优化

考虑上述计算任务存在期限t*，即上述计算任务能够以较大概率在t*时间内完成。一种方式是每个工作节点上放置充分多的编码子矩阵，保证每个工作节点在t*时间内均保持计算状态，这能使得计算完成时间最短；但这种方法带来的存储开销将非常大。另一方面，如果在工作节点上部署过少的编码子矩阵，则可能导致工作节点过早进入闲置状态，从而延长计算完成时间。基于上述考虑，本文提出期限感知的存储优化问题，致力于优化工作节点的存储开销，同时保障计算能以较大概率在期限t*内完成。

令Ri(t*)表示工作节点Wi在t*时刻返回的计算结果数，它取决于启动时延Xi，同时受限于编码子矩阵的存储个数ci，因此为取值不超过ci的随机变量。因此，根据解码条件，计算任务能在期限t*完成的充分必要条件为：

基于此，本文将期限感知的存储优化问题（记为问题P）建模成：

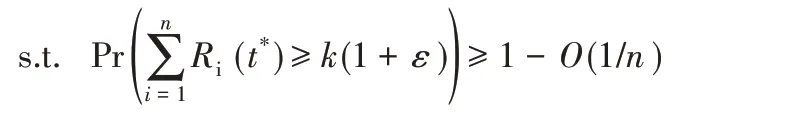
ci＞0，ci为整数

其中，限制条件表示计算任务在t*时间内无法完成的概率不超过O(1/n)，即是1/n的无穷小量。

2 存储优化方案

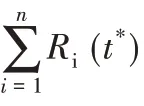
为方便求解，首先引入如下一些自然的假设：

1）异构性受限假设：存在某常数C，使得对于任意的i和j均有，即不同工作节点的计算速度之间的比例受限。

基于上述假设可以发现，存在常数C'使得对于充分大的k，

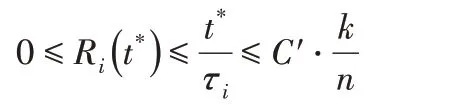
此外，由于Ri(t*)之间是相互独立的，因此，可以应用Heoffding不等式［15］得到：

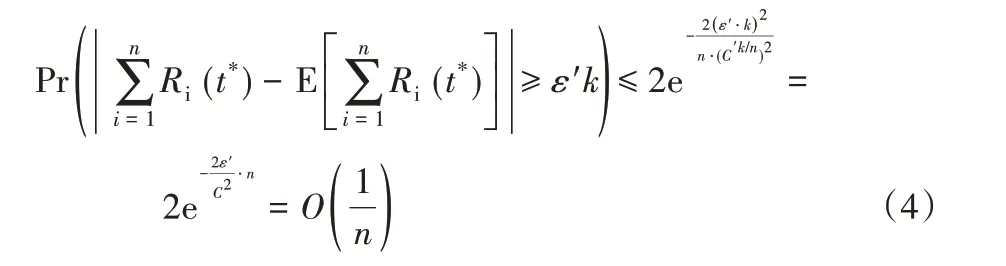
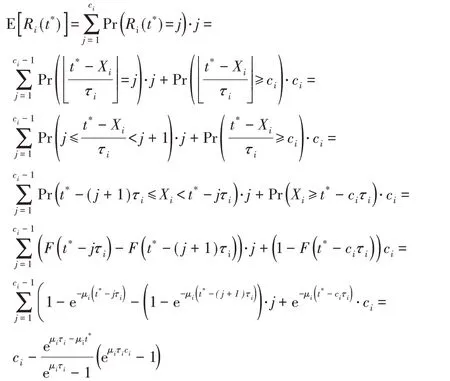
其中，函数F(t)=1-eμit为Xi的分布函数。根据期望的线性性质，有

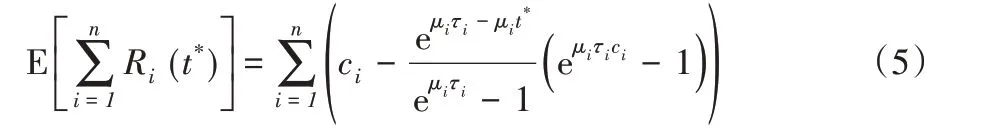
至此，可以将期限感知的存储优化问题转化为如下优化问题（记为问题P2）：

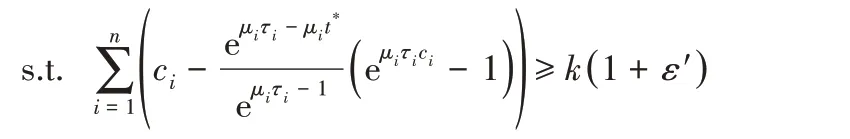
ci＞0，ci为整数

由于上式是整数规划问题，难以直接求解。对ci为整数的条件进行松弛，即考虑ci为非负实数的情形（记为问题P3）：

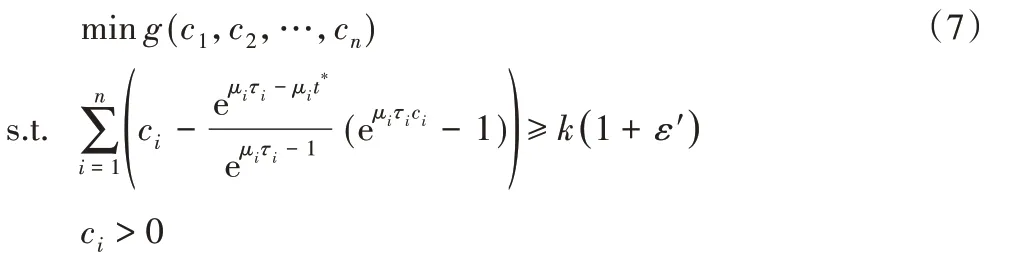
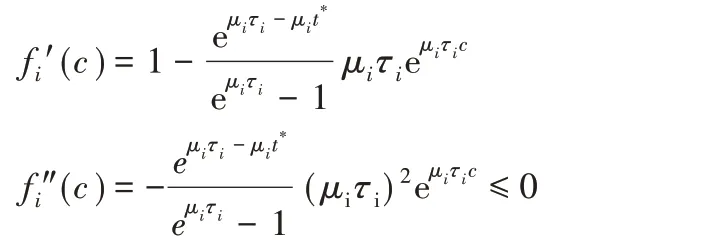
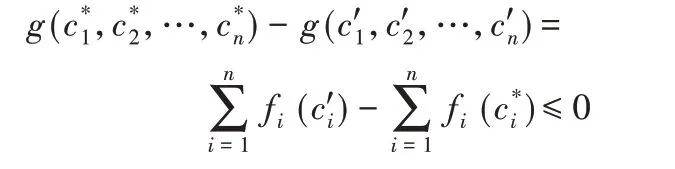
需要补充说明的是，在小规模分布式计算环境中，当n 较小，且ε′取值较小时，基于Heoffding 不等式建立的计算失败概率上限可能会较大。因此在实际应用时，可以通过增加P3的限制条件中ε″的取值去降低计算失败的概率。

3 仿真验证

对于本文提出的存储优化方案，将从两个角度来分析验证：一方面，本文存储方案是期限感知的，所以希望知道随着任务期限放宽，在保证任务完成概率的前提下，本文方案存储开销的变化情况；另一方面，与其他方案进行对比，以验证本文方案在存储优化方面的效果。

3.1 仿真环境

仿真实验在Matlab R2018b工具平台中进行，凸优化求解工具是CVX工具包下的SDPT3求解器。仿真实验中，有20个工作节点和1 个主节点。工作节点的参数，如任务的单位处理时间τi和异构与启动时延参数μi，通过均匀分布采样随机生成，并满足1.2 节中的假设。其中τi从［0.1，1］中随机生成，μi从［0.012 5，0.125］中随机生成。这些设定构成仿真实验的拓扑信息，在一组实验过程中不会发生改变。此外，假设数据矩阵被分成1 000份，即k取值为1 000。

3.2 存储开销变化趋势

根据系统的拓扑信息，给定一个任务完成期限，同时设定一个存储阈值ε″，就可以通过所提方法求得一个存储分配方案，并依据这个方案分配计算任务。计算任务分配成功后，便能进行大量的仿真测试，可以求得本文方案的任务完成成功率。与此同时，可以仿真测得在每个节点上存储无限量的计算任务假设下任务完成的概率，作为任务成功率的上限。可以调节存储阈值ε″，使得本文的存储方案成功率接近任务成功率上限，此时获得的存储方就是最终的优化方案。随机生成两组不同的系统参数，针对一组不同的任务期限，每个任务期进行104次仿真测试，统计其任务成功率，以及优化方案的存储开销（用存储的子矩阵数目表示）。

在两组随机生成的环境下进行了实验，实验结果如图4。可以看出，在保证较大任务成功率（接近任务成功率上限，即每个工作节点均存放充分多的编码子矩阵）的前提下，随着任务期限的逐渐放宽，所提方案引入的存储开销在迅速下降，并逐渐趋向于原始子矩阵个数。根据存储开销的变化趋势，结合实际情形，本文的存储优化方案都可以有较好的收益：对于对任务完成时间要求高的场景，本文方案可以以不超过原始数据2 倍存储的开销，就达到和无限存储接近的任务完成时间和成功率；面对对任务时间要求不高的场景，本文方案只引入了输入矩阵数据量0.2～0.3 倍的额外存储开销，即可以大概率保证计算任务成功完成。同时，对比图4（a）和（b）可以发现，对于不同的系统配置，本文方案的存储开销变化趋势都是一致的。

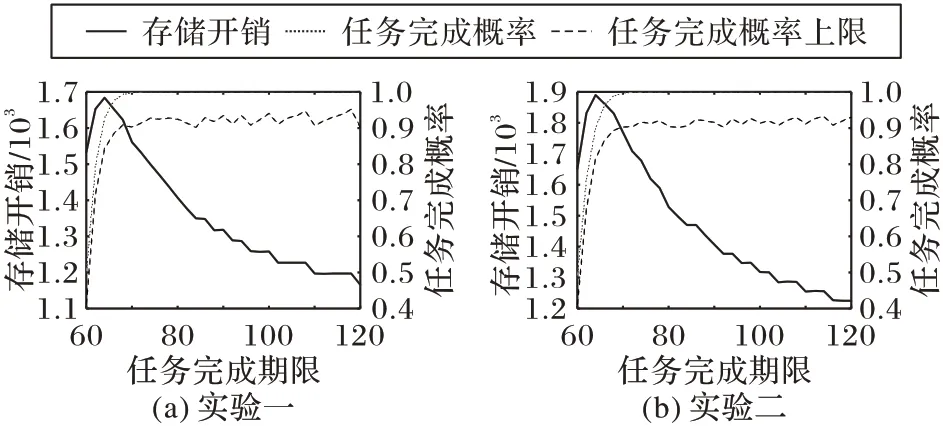
图4 任务完全期限延长下存储开销变化趋势Fig.4 Trend of storage overhead with deadline increasing

3.3 对比实验

该部分实验中，选取了另外两种预先放置策略，并在给定任务期限前提下，比较三种方案的存储开销变化对任务完成概率的影响。三种方案只在每个节点预先存储子矩阵数目方面有所不同，其他方面则保持一致，即均是采用无码率的喷泉码编码，逐步返回计算内容。另外两种对比方案如下：

1）均匀放置方案：每个工作节点放置等量的计算任务。这种方案忽视了工作节点之间的异构性。

2）比例放置方案：按照参数τi即处理速度来按比例分配总的存储开销。这种方案只考虑了不同工作节点计算速度上面的区别，并未考虑启动时延方面的区别。

在一组随机生成的环境下进行了实验，并考虑两个不同的任务期限100 及80。对于不同的存储开销，每个方案均仿真104次求得任务成功的概率，实验结果如图5 所示。从图5中可以看到，随着存储开销的变大，三种方案的任务完成概率均是逐步上升的，其中所提存储优化方案任务完成概率上升速度最快，而比例放置策略则优于均匀放置策略。当任务大概率成功，比如概率取0.9 或者0.95 时，如图5 所示，本文方案带来的冗余存储只有按比例放置方案的一半左右。此外，通过对比图5（a）和（b）可以发现，在任务完成期限较小时，本文存储优化方案与对比方案相比，性能优势更为明显。

图5 三种存储方案下存储开销与任务完成概率对比Fig.5 Storage overheads and task success rates of three storage schemes

4 结语

在考虑存储开销与计算完成时间之间的权衡关系的基础上，本文对面向异构工作节点的计算期限感知的存储优化问题进行了建模，并基于理论分析，提出了基于期望近似的解决思路，进而通过松弛将问题转化为凸优化问题进行高效求解。仿真实验结果表明，本文存储方案与其他方案相比，能够大幅度降低编码带来的额外存储负载。由于很多实际应用中数据被建模成稀疏矩阵，因此未来还将进一步探讨面向稀疏矩阵-向量相乘的高效存储方法。