让学生经历数学发现之旅——记一堂“两位数乘两位数”的练习课

□沈秋红

教学人教版三年级下册“两位数乘两位数”时，有学生出现21×19=20×20=400这样的错误，把加法计算中移多补少的方法误用到乘法算式中。笔者反思了自己的教学：学生对乘法计算的算理是否理解？根据以上错例，笔者设计了一节“两位数乘两位数”的练习课，并与“面积”单元的内容相整合，制定了如下教学目标：通过比较，发现两个因数和相等的这类乘法算式的变化规律，并能根据规律比较积的大小，根据规律进行计算；数形结合，有效理解乘法计算与图形面积之间的关系，感受数学的魅力。

浙江省数学教研员斯苗儿老师说：数学教学应遵循“学生立场、单元视角、有机整合、适度拓展”的原则。这堂课笔者站在学生的立场设计练习，把相关联的知识整合起来进行教学，既关注基础，又适度进行拓展。课堂上，学生积极参与，深入思考，积极性高，学习效果好！

一、立足学生立场，落实基础，开拓思维发展

【教学片段1】

教师出示如下情境：

学校组织三年级学生看电影，共398 人，下面哪个电影院比较合适？

①号影院：有21排座位，每排可容纳19人。

②号影院：有22排座位，每排可容纳18人。

③号影院：有23排座位，每排可容纳17人。

估一估每个电影院大约有多少个座位；算一算每个电影院的准确座位数。

学生通过先估算再列竖式计算得到三个影院具体的座位数。

①号影院：21×19=399。

②号影院：22×18=396。

③号影院：23×17=391。

显然，选择①号影院比较合适，因为另外两个影院的座位数小于学生人数。

教师应通过让学生估一估，帮助他们养成先估再算的良好习惯，提高计算的正确率。观察学生的估算方法，主要有两种：两个因数都估、只估其中一个因数。再经过计算，使两位数乘两位数的笔算方法得到巩固。不足之处在于“能结合具体情境进行估算”这一子目标未能较好体现。在具体情境中估算，要考虑估大估小的问题，从这一点考虑，本组材料中的数据可以再作调整，使教学目标更加细化。

师：谁来猜一猜，接下来老师会出一道怎样的算式?

生：24×16。

师：估一估这个算式的结果。

生：大约是400，但比400要小。

生：我觉得比391还要小。

师：到底是多少，需要摆一摆竖式。

计算后得出结果：24×16=384。

这时黑板上共有5个算式：

20×20=400；21×19=399；22×18=396；23×17=391；24×16=384。

师：仔细观察这组算式，你能发现什么规律？

生：我发现两个因数的和一样，都是40，而差不相同。

生：一个因数在逐渐变大，另一个因数在逐渐变小。

生：我发现积越来越小了……

小结：在这组算式中，两个因数的和相等，这两个因数越接近，积就越大，否则就越小，可以用下面的图形（大小）来表示。

通过观察与比较，学生明白和相同的两个因数，积可以不相同，这与周长相等的长方形面积可以不同是同样道理。

二、巧用生成资源，调整策略，捕捉智慧亮点

【教学片段2】

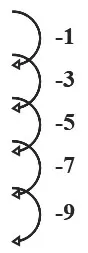
生：我发现算式的得数有规律地在变化。400到399 少1，399 到396 少3，396 到391 少5，391 到384 少7。接下来就是少9，所以我能直接说出25×15的答案，384-9，是375。

学生的发现马上就得到了其他同学的共鸣：是的是的，我也发现了，这样我们还可以直接计算26×14，27×13……这些算式的结果了。

板书整理： 20×20=400

21×19=399 22×18=396 23×17=391 24×16=384

小结：（两因数）和相等的一组乘法算式，其中一个因数逐渐变大（或变小），积逐渐小1，小3，小5，小7，小9……

师：刚才这位同学发现的这个规律很有用，但是不是所有这样的一组算式都适用这个规律呢？

生：老师，你给我们出一组类似的算式，我们先根据规律计算，然后再列竖式来验证下就行了。

师（把问题抛给学生）：那谁能给我们出一组这样的算式呢？

（学生兴趣盎然，都举手要求给大家出题目。教师要求同桌合作，一生出题一生说答案，然后列竖式验证得数的正确性。之后教师出示以下两组算式）

①根据25×25=625，计算：

26×24= 27×23= 28×22= 29×21=

②根据50×50=2500，计算：

51×49= 52×48= 53×47= 54×46=

大部分学生都能直接写出结果，很是得意。

课堂上教师要善于捕捉学生智慧的闪光点，引导学生进一步思考，深入讨论，并进行适当的归纳与对比。两位数乘两位数和相等的这组算式，学生不仅判断出积的大小关系，还找出前后两个算式间的关系与规律，充分发挥了主观能动性。

三、善用再生资源，深度思维，丰富细化目标

【教学片段3】

课上到此时教师准备告一段落，学生也沉浸在收获的喜悦中，这时传来一个弱弱的带着质疑的声音：如果两个因数离50 比较远的话，算起来很麻烦。如计算55×45，还得把前面的算式都写出来，太麻烦了，还不如直接写竖式。

课堂再次变得安静，学生似乎都在思考这位同学提出的问题，并陆续有人点头表示认同。

教学要舍得给学生思考的时间，安静之后一定会有爆发。一分多钟之后，课堂上出现了几只高高举起的小手。

生：老师，我有办法了。不用写出55×45 前面的算式，也能直接计算它的答案。

师：很期待你的想法!

生：只要把下面的算式都和第一个算式去比较就可以了，比如21×19=399，20×20=400这两个算式中的第一个因数21 与20 相差1，得数399 与400 相差1；同理22×18=396，20×20=400 中的第一个因数22 与20 相差2，得数相差4（2×2=4）；23×17=391，20×20=400 中的23 与20 相差3，得数相差9（3×3=9），所以计算55×45，我们只要看第一个因数55 与50 相差几（5），得数就相差几乘几的积（5×5=25），只要用2500-25就可以了。

其他同学纷纷列竖式验证其正确性，课堂上自觉地响起了热烈的鼓掌声。

板书整理：

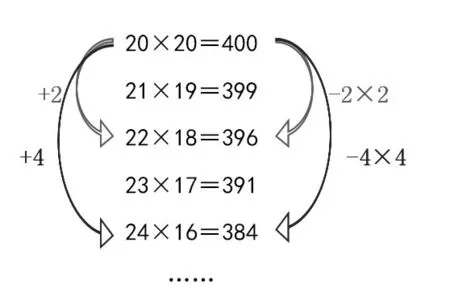
小结：（两因数）和相等的一组乘法算式，与两个因数相等的算式相比，其中一个因数增加（或者减少）几，积就减少几乘几的积（即几的平方数）。

生：老师，我能计算59×41=50×50-9×9=2500-81=2419（参考50×50）。

生：我知道36×44=40×40-4×4=1600-16=1584（参考40×40）。

生：27×23=25×25-2×2=625-4=621（参考25×25）。

……

教师布置课后作业：

①根据35×35=1225，

计算36×34=1225-（ ）=（ ）

37×33= 38×32= 39×31=

②根据89×89=7921，

计算92×86=7921-（ ）=（ ）

95×83= 97×81=

③直接写出答案63×57= 106×94=

④（ ）×（ ）=（ ）

教师应鼓励学生创造性地提出意见，善于发现各种有价值的资源（再生资源），给学生提供进行质疑、争论、反驳的机会，并适时加以引导点拨，作为“即时目标”，打造具有高阶思维的课堂。

四、数形结合，回归整体，强化学习效果

【教学片段4】

“两位数乘两位数”的下一单元就是“长方形正方形的面积计算”，如何践行计算教学与空间图形的有效结合。结合本课例，对于“周长相等的长方形，长和宽越接近，面积就越大”显然可以解释得更加到位；同时也是对前面发现的规律的实际应用。

教师出示思维练习：王大伯用24 米长的竹篱笆围一块菜地，怎样围面积最大（注：长和宽都是整米数）？

用24 米长的竹篱笆围长方形，也就是长方形菜地的周长是24米，那么长加宽等于12米，表格呈现以下6种情况。

周长（米）24长（米）6 7 8 9 10 11宽（米）6 5 4 3 2 1面积（平方米）6×6=36 7×5=35 8×4=32 9×3=27 10×2=20 11×1=11

观察面积这一列算式：

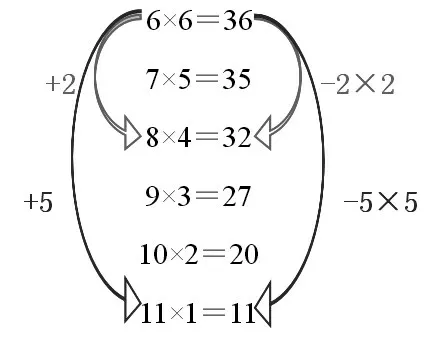
得出结论：

①当长为11 米，宽为1 米时，长和宽相差最大，面积最小，是11平方米。

②当长为6米，宽为6米时，长和宽最接近（此时刚好是一个正方形），面积最大，是36平方米。

③跟正方形边长相比，长（或者宽）相差1 米，面积就相差1平方米，长（或者宽）相差5米，面积就相差25（5×5）平方米。

图形呈现（单位：米）如下。

7×5=35。把6×6 正方形最下面的1 排小正方形（6 个）旋转90°拼接到右边，结果多出一个小正方形。

8×4=32。把6×6 正方形最下面的2 排小正方形旋转90°拼接到右边，结果多出4个小正方形。

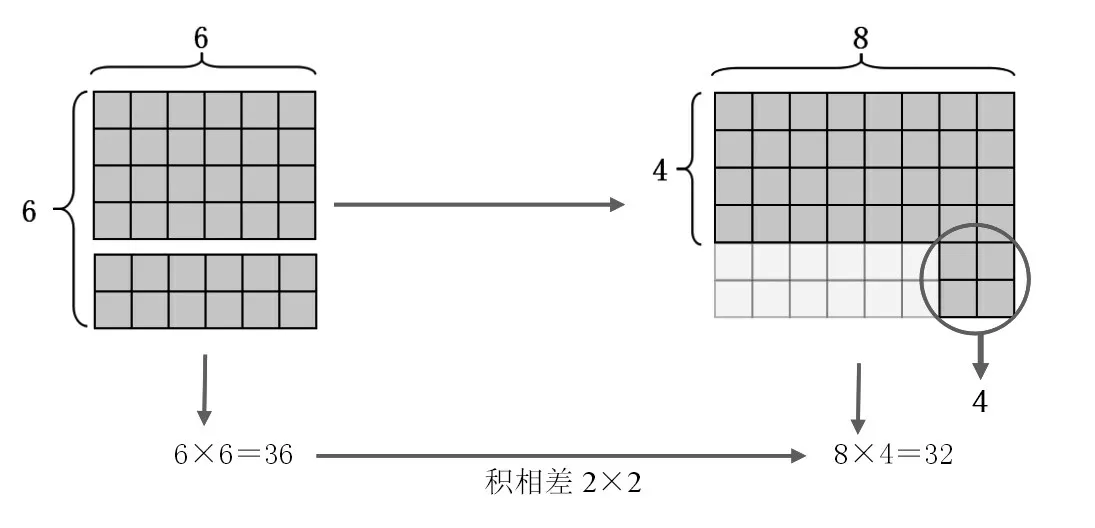
继续拼接下去，就会多出9（32）个，16（42）个，25（52）个小正方形。

教师出示拓展练习：李阿姨家有一块用竹篱笆围成的长方形菜地，长36 米，宽28 米，现在要进行改建，要求在不增加材料的情况下增加菜地的面积，可以吗？最多能增加多少平方米？

经过计算最多能增加：4×4=16（平方米）。

如果用字母式表示，就是：

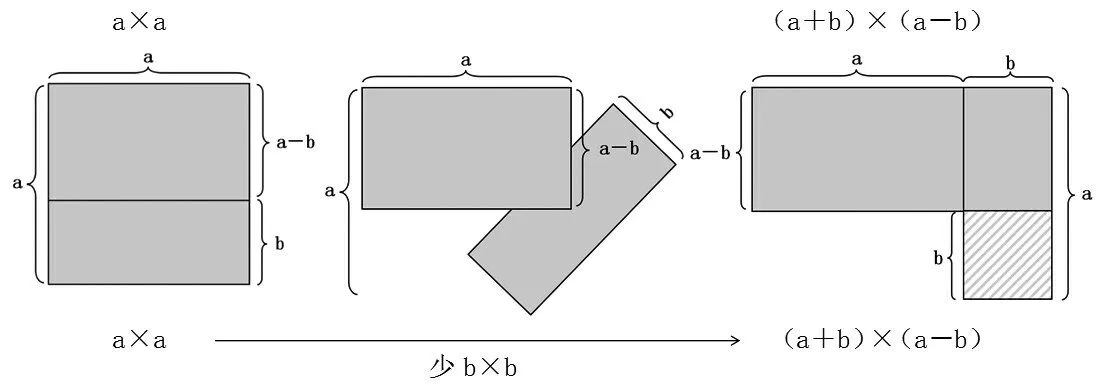
可得到a×a-b×b=（a+b）×（a-b），即平方差公式。

两位数乘两位数，学生发现了三条规律，由浅入深，结合这三条规律，用数形结合方式进一步加以验证巩固，同时也使得周长和面积的关系因为有算式的支撑更加明确，更加丰富。学生明白了随着长和宽的变化，面积是如何变化的，体现了数形结合的思想，学生感悟到知识之间是相互连通的。

学生经历的数学发现之旅，是他们高阶思维发展的体现。