“图解数学”，“小老师”的好帮手

□陈 云

“小老师”是近年来出现的一种新型教学方式。它一方面可以更好地彰显学生的主体价值，激发学生自身的学习主动性和学习潜能，另一方面也能更好地发挥同伴互助的教学功能。“图解数学”是用图或画的方式来解释数学的结论或原理，实现小学生数学思维可视化的一种有效方式。它是学生相互交流、自主建构的重要载体，可以成为“小老师”分析讲解、反思修正的常用手段，从而促进自身数学能力的提升，也有助于启发其他同学。

一、图解数学让“小老师”的见解清晰可见

让学生做“小老师”是落实学生主体地位的一种做法。每个学生都希望有机会当“小老师”，为了获取这样的展示机会，学生会主动、积极地对外部信息进行深度认知以及再加工。这一过程看似简单，其实对数学信息从初步感知到完全理解，再到外化展示，对于小学生来说是一个极其复杂的过程，需要“小老师”进行辨别、比较、判断和加工。要较好地完成这一任务，学生除了要具有良好的语言基础外，还必须掌握必要的技巧。“图解数学”就能恰到好处地帮助学生对数学信息中的内容进行有效梳理，例如：借助图示提取重要数学信息、借助图示表征关键的数量关系等。

在苏教版二年级上册“认识平均分”的教学中，教师追问：什么是平均分？对于这样的问题，学生有“似曾相识”的熟悉，也有“雾里看花”的模糊，如果要求“小老师”来谈谈自己的想法，不借助一定的外显形式，确实很难表述，学生说来说去就是一句“分得同样多”，再不知如何解释。这样的回答并不足以让其他同学有更多收获，也很难对除法的意义和除法可能存在的两种情况（平均除、包含除）进行有效区别。但如果我们把这样一个宽泛的问题让学生用图解的方式使其具体化、形象化：“什么是平均分？把你认为是平均分的故事写出来或画出来。”学生从自己的生活中去搜索平均分的实际问题，然后努力选择合适的表征方式把问题记录下来，在作业展示环节，“小老师”有了抓手，讲解起来就会底气十足：“妈妈买来12颗糖果，如果哥哥、我和妹妹每人分得的同样多，我们每人可以分到4颗糖果。你看，我们3 个人要分得同样多，这就是平均分，可以说是平均分给哥哥、我和妹妹。”“张老师有8只气球，每人给2只，张老师的气球可以分给几个人？每人2只就是你2只、他2只、我也2只，一直分，分给了4 个人，这样每个人都得到2 只，就是同样多，所以叫平均分（如图1）。”……很显然，有了图解，“小老师”的表达就显得“有血有肉”、活灵活现，对低段学生建立“平均分”的表象很有帮助，也能启发其他同学想到各种平均分的实际问题。

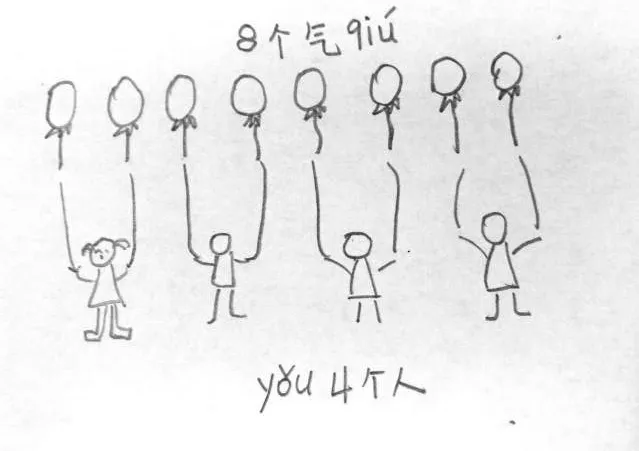
图1

小学生的思维是由具体形象思维逐渐发展为抽象思维的一个质变的过程，需要一定的教学手段和工具媒介助力。一些直观的图示、表格在学生思维转变中能起到重要的作用。如上，凭借直观的图解，学生对抽象的“平均分”问题有了真实的、可触摸的理解。

二、图解数学让“小老师”的分析丝丝入扣

直觉是指在经验和已有知识的基础上，不经过逻辑推理而直接迅速地认知事物的思维活动。在数学学习过程中，学生很容易用“直觉”判断一个结论是否正确，习惯于遵从“直觉思维”模式，不太愿意对数学问题做理性分析。之所以出现这种情况，是因为“直觉”也会在很多时候让学生做出正确的判断，这固化了学生的“直觉规律”，相应的也导致学生发生一些常见的错误。教师要寻求一种方式让学生养成一种良好的习惯，即在自己没有完整思考的情况下，不轻信、不盲从“直觉”的答案。“图解数学”就是一种可用的方式。“图示”作为一种特有的数学语言，既可以解释概念，也可以对解题策略进行分析，一定程度上能帮助学生克服错误的直觉反应，让问题的分析过程和推理过程更有深度。

例如苏教版五年级上册“小数的再认识”的教学，教师要帮助学生真正理解小数，感知小数的记数是“位值记数法”的拓展，小数是遵循整数记数规律的一种新的数。但是，如果只是简单地进行十进分数与小数的互化，“小老师”恐怕自己都未必明白为何等于0.72，只是凭直觉说出7分米2厘米=米=0.72米，这不是思考的结果，而是依照教师之前给出的情景，“套路”出的答案。那写成三位小数，是0.072 还是0.720 呢？为了帮助“小老师”进行理性分析，教师可为学生创造“图解数学”的经历：用米尺测量出张老师的身高，并用小数表示出来，也可用其他图示解释你的思路（如图2）。有了“图解”的经历，“小老师”的分析便能入“理”三分：“我是这样想的，10米平均分成10份，每份就是1 米，1 米平均分成10 份，每份就是0.1 米，7 个0.1米就是0.7 米；接着往后分，这里有点小，看不出来了，但我们可以想象，0.1 米再分就是0.01 米，因为它们都是10份、10份地分下去的，这里大约是2个0.01米，全部合起来就是1.72米。”（如图3）“我觉得1米平均分成10份，1份就是米，也是0.1米，0.1就是1的个0.1米就是0.7米；再往后把0.1平均分成10 份，其实就是把1 米平均分成100 份，每份是米，也就是0.01 米就是0.01，2 个0.01米就是0.02米。我觉得好像还多了一半，这里分不下了，我把它画在右边。我们可以想象一下，0.01接着平均分，每份应该是0.001米，我感觉在中间，就算5份吧，那就是0.005米，合起来就是1.725米。这里的0.1，0.01，0.001之间都是10倍、10倍的关系，和还有整数的1000，100，10，1之间的关系都是一样的。”（如图4）

图2

图3

图4

“图解”过程中，“小老师”的思考路径清晰可见，能借助平均分的操作，把尚未正式学习的小数单位解释得不那么抽象了。因为学生很巧妙地把小数这种计数方式和整数进行了有效的沟通，10份、10份地逐次分下去，也就从左往右逐次排列下去，成为0.1，0.01，0.001。再结合十进分数的结构来解释小数，把整数、小数、分数进行了联系，实现了零散知识体系化。当图示中0.01平均分成10份时，学生没办法画了，但能根据相应的原理进行想象，推理出接下来分的过程和结果，可见学生的分析已经突破“直觉”，较好地弥补了文字描述无法在大脑中呈现清晰图像的缺陷，很大程度上提升了“小老师”讲解的效果。

三、“图解数学”让小老师的反思有据可依

维果茨基说过，人所特有的心理过程都是由语言、标志和符号这样的心理工具充当中介的，这种以符号系统为中介的高级心理机能需要由外部集体活动内化而成。也就是说，学生最初是有自己的想法的，这些想法可能对、可能错，也有可能是“半对半错”，不足以实现从知识的理解到策略的形成。策略的形成需要经历一个过程，在这个过程中需要自我的反思和与同伴的交流。学生参加小组或全班的学习活动，须借助各种符号展开交流，以帮助学生实现自我完善。

例如在“平均数”问题的教学中，小学阶段较为常见的算术平均数的计算，就是两个数的算术平均数个数的算术平均数受到算术平均数算法的影响，在“用单价10元的牛奶8千克和单价5元的果汁2千克，混合成牛奶果汁，每千克应该以什么价格出售？”这类加权平均数的问题中，一位“小老师”振振有词地表达了自己的观点：这里是求价格的平均数，所以只要找到价格10元和5 元就可以了，（10+5）÷2＝7.5 元，应该以7.5元的价格出售。对于这样的讲解，学生中渐有唏嘘声，很显然，原来仅8千克牛奶就要80元，现在加上果汁才75 元，一定有问题。可是，问题出在哪里？算术平均数的算法根深蒂固地缠绕着学生的思维，学生必须借助图解，把整个思路重新梳理，才能“破茧成蝶”。于是，教师引导学生反思：结合平均数学习的过程，画出10千克果汁牛奶的价格如何平均。有“小老师”从平均数最初学习时用到的“移多补少”中受到启发，给出了如图5的解释，这给其他同学一个启发：原来这里不是1 个10 元和1 个5 元平均，而是8 个10 元和2 个5 元在平均。其他的同学也逐渐打开思路，给出了如图6 的解释，这为平均数的计算过程（10×8+5×2）÷10做了很好的直观诠释。借助思考路径的图解过程，“小老师”终于意识到最初的“振振有词”是欠缺考虑的，并真正接受和理解了加权平均数与算术平均数的“异”与“同”。

图5

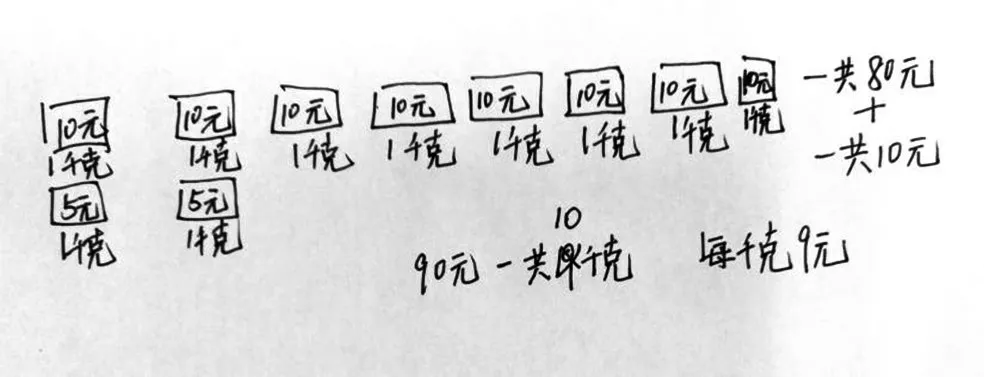
图6

“小老师”登上舞台，借助“图解数学”，用直观的图形显化思维，在合作交流中用精准的语言阐述思考过程，能发展学生的数学思维，提升学生的数学能力。