猜想—验证，有助于培养学生的高阶思维

□胡艳英

在小学阶段，教师应设法让学生提出自己的观点并进行佐证，有理有据地说出自己的想法、做法，得出相对应的结论。这样的训练可以促使学生的思维更加严谨，有深度。

一、臆测教学的启示

台湾清华大学林碧珍教授倡导的小学数学臆测教学，其基本理念就是“有多少证据说多少话”。学生在学习新知识时，会在教师的引导下经历“造例—提猜想—效化—一般化—证明”这一系列学习过程，积累丰富的学习经验。

（一）案例再现：“圆的面积计算”

关于圆面积公式的推导，林碧珍团队的教师花了四节课的时间进行实践。执教教师为学生提供了等分成不同份数的圆形纸片，供学生选择进行探索造例，用已学过的平行四边形、梯形、三角形的旧知来计算出圆的面积。

圆形纸片等分的情况有如下几种：3等分，4等分，5 等分，6 等分，7 等分，8 等分，9 等分，10 等分，13等分，16等分。

学生选择上述一种进行剪拼研究，拼成已学过的图形，尝试计算出圆的面积，然后在小组内进行交流。

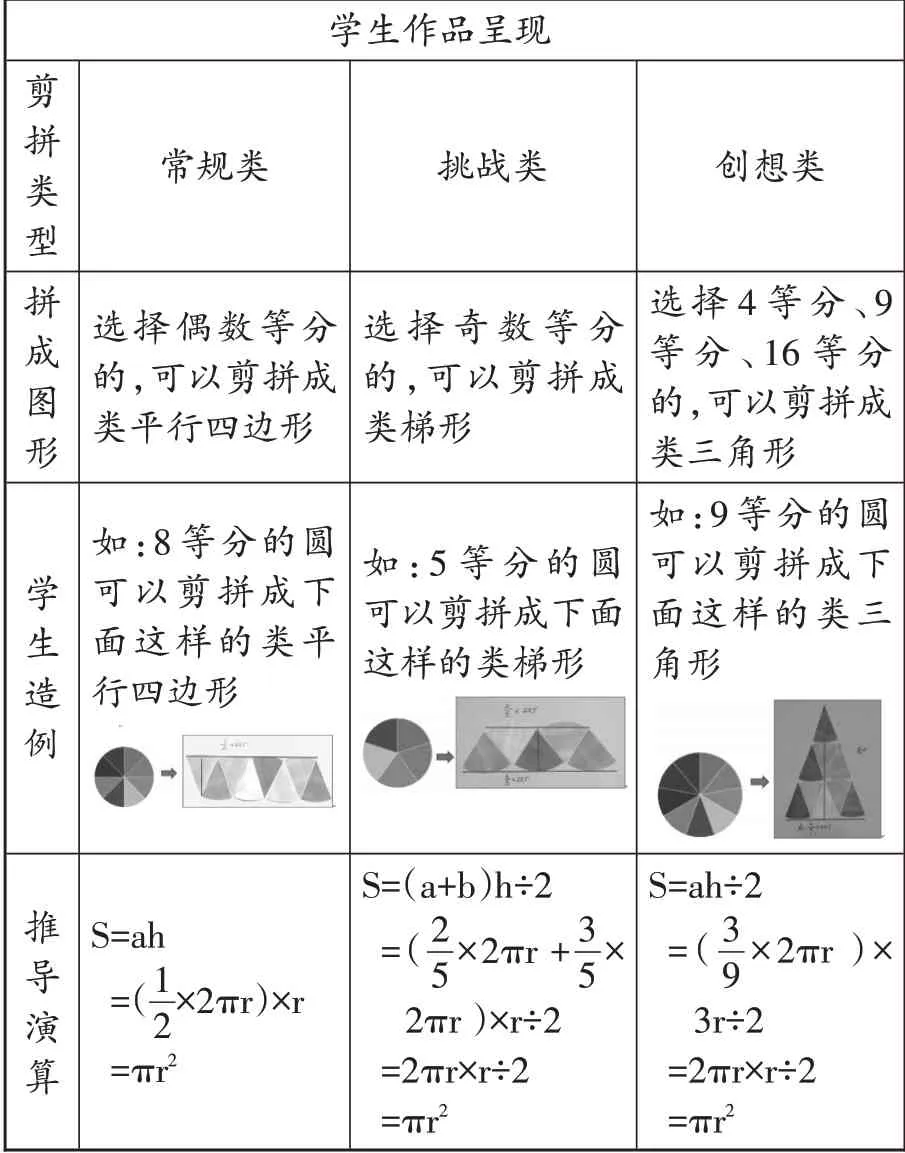
学生作品呈现剪拼类型拼成图形 学生造例 推导演算常规类选择偶数等分的，可以剪拼成类平行四边形如：8 等分的圆可以剪拼成下面这样的类平行四边形images/BZ_40_1373_2127_1616_2218.pngS=ah=（1 2×2πr）×r=πr2挑战类选择奇数等分的，可以剪拼成类梯形如：5 等分的圆可以剪拼成下面这样的类梯形images/BZ_40_1642_2098_1907_2197.pngS=（a+b）h÷2=（2 5×2πr +3 5×2πr）×r÷2=2πr×r÷2=πr2创想类选择4 等分、9等 分、16 等 分的，可以剪拼成类三角形如：9 等分的圆可以剪拼成下面这样的类三角形images/BZ_40_1936_2098_2166_2246.pngS=ah÷2=（3 9×2πr）×3r÷2=2πr×r÷2=πr2

小组派代表将猜测的结论在全班同学面前阐述。最后，教师对每一种猜想进行引导剖析。学生发现每一种情况最终都会用“半径×半径×3.14”来计算，从而得出圆面积的计算公式。研究到此并未结束，教师接着抛出问题：什么时候可以拼成大三角形来计算，有个数限制吗？个数有什么特征？引导学生发现，只有当一个圆平均分成完全平方数的个数时，大三角形才可拼成。

（二）观课启示

从“学习效果”的角度看，学生完全投入新课的学习之中，每个人都有自己的想法和收获，在分享自己观点的同时也吸纳别人的不同方法，学习这件事情在每个学生身上真实地发生。虽然学习过程看起来缓慢，但学生亲历其中，人人思考，参与猜想，见证了知识的形成。在这节课中深深体会到学生是探索的主体，教师是“顾问”和“引路人”。

从“学习方法”的角度看，每个学生都有自己的选择权，选择自己喜欢的学习材料，剪拼成自己喜欢的熟悉的图形来探究，没有强制性规定，没有单一式灌输。在学习过程中，学生有丰富的想象空间，他们按自己的想法剪拼成类平行四边形、类梯形和类三角形，都近似地计算出圆的面积。最后归纳导出圆的面积计算公式是“S=πr2”。

由此可见，对于小学中高段学生，教师可以进行猜想—验证教学。

二、教学尝试：让学生在猜想—验证中获取数学思想

认知心理学派强调，学习中要学会质疑。教师要引导学生在探索中提出问题，从而加深对知识的理解，提高学习能力。为此，在教学中，教师应鼓励学生大胆质疑。

（一）操作证伪：“难成平行四边形”

浙教版六年级下册数学《作业本》“圆柱的侧面积“练习三第1题是这样的：

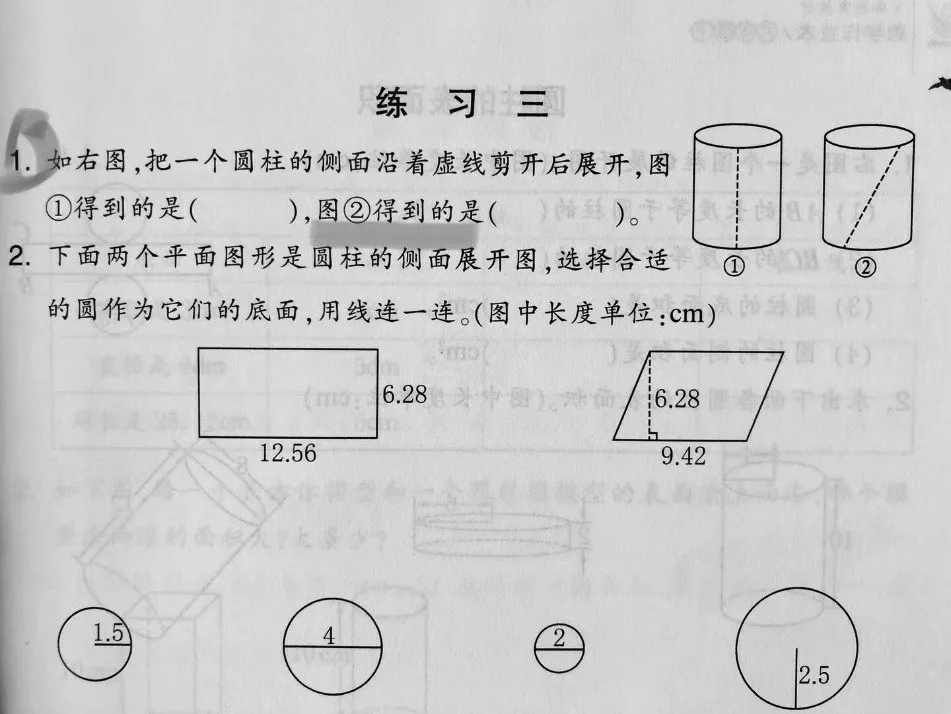
有学生在解答时提出：图②这条虚线这么直是不科学的。

教师追问：为什么这么说？

学生上台边演示边说明：我们用软三角尺贴住侧面，假设这是那条线，您看，这条线画在平面上不可能是直的，软尺在曲面上，这条线必定有弧度。

（说明：三角尺太硬了，用长方形纸条来围，它薄一点更能贴牢，这条边的弧度更加明显。）

生：如果非要做这道题，沿图上的直直的虚线来剪，那我只能填近似的平行四边形了。

这是一次课后练习中发生的小插曲，学生证伪成功，数学学习的自信瞬间提升。

（二）计算验证：“格点法可用于多边形面积计算”

学生一旦有了证明（验证）的意识，思考问题的方式就会跟着发生改变。学生有了强烈的质疑和求证的意识，其日常的学习会变得很不一样，思维就会慢慢走向高阶。

如教学人教版五年级上册第六单元“多边形的面积”时，在完成基本教学任务的前提下，教师让学生思考验证“格点法是否可以解决多边形面积计算”（格点多边形面积=内格点数+边格点数÷2-1）。学生带着疑问开始学习。

学生小组合作，验证过程如下：

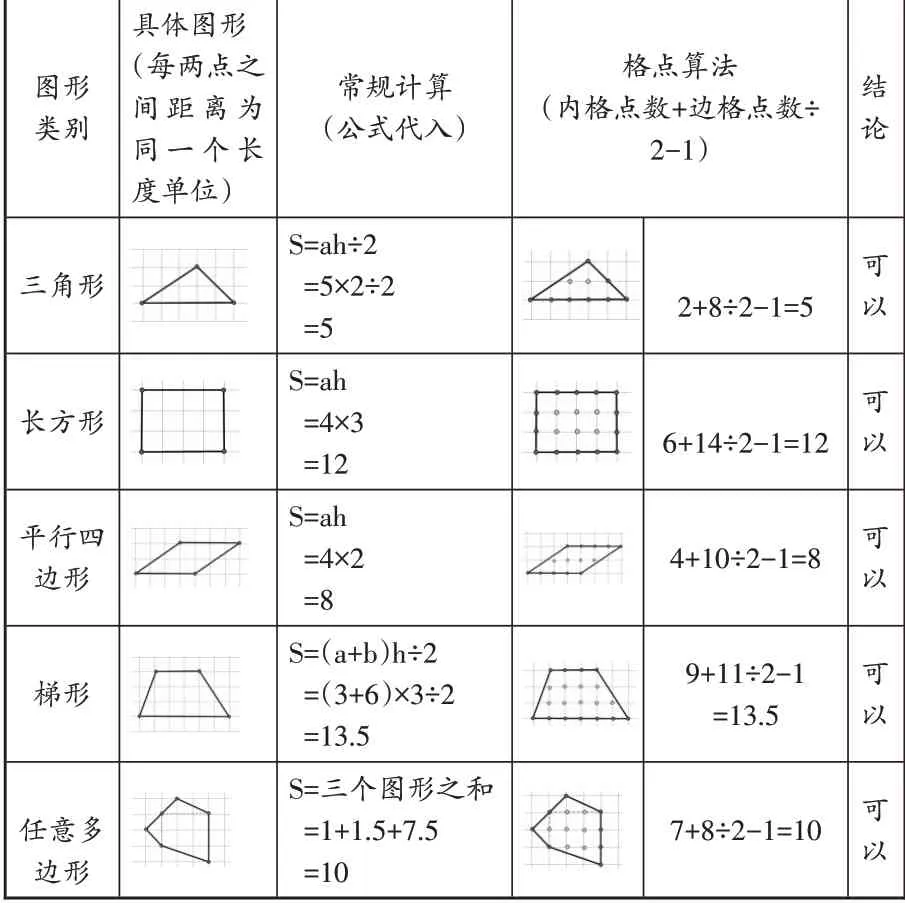
图形类别三角形长方形平行四边形梯形任意多边形具体图形（每两点之间距离为同一个长度单位）images/BZ_41_1411_1953_1526_2026.pngimages/BZ_41_1411_2085_1519_2167.pngimages/BZ_41_1411_2232_1527_2291.pngimages/BZ_41_1411_2360_1520_2436.pngimages/BZ_41_1411_2497_1509_2570.png常规计算（公式代入）S=ah÷2=5×2÷2=5 S=ah=4×3=12 S=ah=4×2=8 S=（a+b）h÷2=（3+6）×3÷2=13.5 S=三个图形之和=1+1.5+7.5=10格点算法（内格点数+边格点数÷2-1）images/BZ_41_1804_1955_1919_2024.pngimages/BZ_41_1804_2086_1911_2165.pngimages/BZ_41_1804_2236_1905_2288.pngimages/BZ_41_1804_2366_1916_2429.pngimages/BZ_41_1804_2495_1901_2572.png2+8÷2-1=5 6+14÷2-1=12 4+10÷2-1=8 9+11÷2-1=13.5 7+8÷2-1=10结论 可以 可以 可以 可以 可以

经过验证，小组讨论得到结论：格点法可以解决多边形面积计算的问题。（注：多边形应为格点多边形）

（三）图解揭秘：“首同尾合十”的两位数乘法巧算原理

乘法125×8 可以巧算，还有一些也可以巧算。比如23×27，可以用“头×（头+1）”也就是20×30+“尾×尾”也就是3×7 来计算等于621，这就是“首同尾合十”的两位数乘两位数的巧算。为什么呢？教师可以提供相应的学习材料让学生操作思考。

过程模型呈现立论验证尝试应用探究数形结合举例23×27=20×30+3×7=621①39×31=30×40+9×1=1209 √②54×56=50×60+4×6=3024 √③43×57=40×60+3×7=2421×④27×26=20×30+6×7=642 ×①39×31=30×40+9×1=1209images/BZ_42_423_1615_667_1808.pngimages/BZ_42_676_1614_874_1808.pngimages/BZ_42_491_1821_816_2026.png③43×57=40×60+3×7=2421images/BZ_42_425_2449_657_2623.pngimages/BZ_42_667_2449_881_2623.pngimages/BZ_42_465_2635_842_2864.png形成观点可以用“头×（头+1）”也就是2×3作积的前两位，“尾×尾”作积的末两位计算发现①②的结果是正确的，③④的结果是错误的。说明并不是所有的两位数乘两位数都可以这样来计算①②符合“首同尾合十”，从拼组的过程中可以看出，左下角的一块拼到了图形的右边，长方形的长就正好多了10 个单位，宽不变，面积正好是“头×（头+1）”，此时，还剩下右下角的一个小长方形，长和宽分别为原算式中的个位上的数，也就是“尾×尾”，两个长方形面积之和，就是原长方形的面积与上同样操作，发现“头×（头+1）”40×60 可以实现，“尾×尾”3×7 出现，但是此时的图形面积并不止是这两部分之和，还多了右下角圆圈中的一部分。这种情况与“首同尾合十”算法不符，因此不能用相同的算法计算

学生利用图形，证明理解了巧算的原理，体验了成功的喜悦，同时使观察、质疑、推理、归纳、应用等高阶思维能力得到了锻炼。

三、数学教学要指向高阶思维的培养：在猜想验证中从“是什么”走向“为什么”

所谓高阶思维，是指发生在较高认知水平层次上的心智活动或认知能力，主要指创新能力、问题求解能力、决策力和批判性思维能力。

对小学生来说，经历归纳、猜想、证明（验证）等过程是培养高阶思维能力的有效举措。教师授课不但要让学生明白“是什么”，而且要让他们明白“为什么”。

如人教版三年级下册P65，P75 分别有两道练习题，一道是周长相等画不同的长方形，另一道是面积相等画不同的长方形。两题均有让学生思考的要求“你能发现什么”。这类练习课，教师都会直指规律，那就是“周长相等时，长与宽越接近，面积越大；面积相等时，长与宽越接近，周长越小”，让学生初步感知这个规律。如果教学止步于此，学生脑海中留下的仅仅是问题的结论。教师不妨放手让学生进一步探索证明“为什么会这样”，引导学生的思维趋向高阶。

教师出示改编后的学习材料供学生探索。

1.下面每个小正方形的边长为1 厘米。在方格纸上，画出周长为24 厘米的长方形，你能画几个？（1）独立在方格纸上画一画。（2）小组合作，在记录表中有序理一理。（3）思考：周长不变时，面积怎么变？为什么？

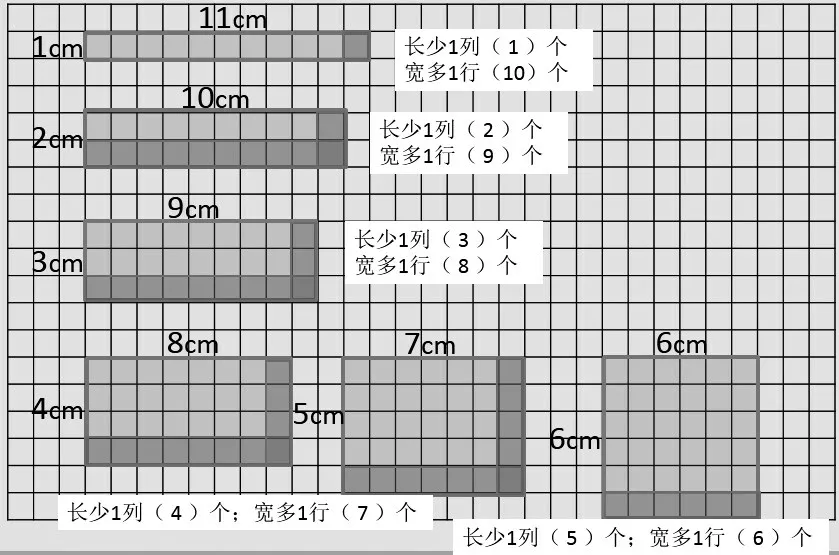
2.三（1）班要设计一面长方形笑脸墙，现有1平方分米的正方形照片20 张，有多少种不同的摆法？如果给照片墙配上边框，怎样最节省材料，为什么？

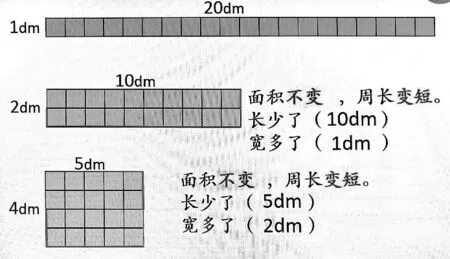
教师引导学生在图形对比、数据对比中层层深入，不断挖掘知识的内涵，让学生不断经历变与不变的归纳推理证明（验证）过程，促进学生高阶思维能力的提升。