循“生长”之道，从“原点”走向“远点”——例谈“生长课堂”的教学策略

□陆李华

生长课堂关注生命、联结生活、注重生成，是激发学生不断萌生想法，创生智慧，共生发展的理想场所。数学课堂应遵循儿童的生长规律，成为开阔、纵深的思维对话场，教师要善于巧妙点化，引领学生经历有意义的数学学习历程。数学生长课堂既要关注学生当下的学习状态，又要着眼于学生未来数学学习和生活的发展远点。笔者结合“图形的放大与缩小”的教学，谈谈“生长”课堂之道。

一、生长课堂应植根于生长的“原点”

美国心理学家奥苏伯尔认为，所有的教育心理学原理可还原为一句话，“学生已知了什么，从这里出发进行教学”。生长课堂的第一要义，就是要精准把握学生的生长“原点”。

【教学片段1】

师：马上就要到圣诞节了，老师制作了一张电子贺卡，一起看！（课件动态演示图片的旋转、平移）

师：图形先后经历了怎样的运动变化？

生：先旋转，再平移。

师：对！平移和旋转是图形变换的两种方式，我们以前就研究过。那么在刚才图形变换的过程中，图形的什么变了？什么没有变？

生：图形的位置变了。

生：形状和大小都没有变。

师：真会观察！同学们，今天我们再来学习一种图形的变换方式——图形的放大和缩小。（板书课题）

师：还是看这幅图，为了让后排的同学看得更清楚，我打算把它放大一些。你觉得该怎样放大呢？

生：可以拖动鼠标把图片拉大些。

（教师通过电子白板操作，将图形分别横向拉大、纵向拉大，整体放大）

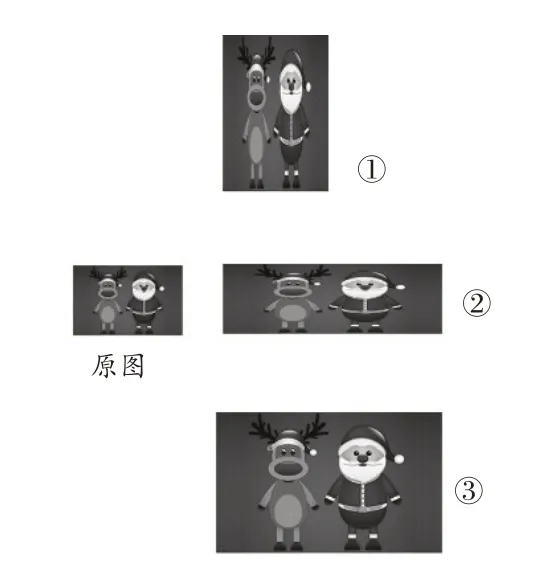
师：图①、图②、图③都变大了，你觉得它们都是放大吗？

生：我觉得图①、图②不是。这两幅图虽然变大了，但有点怪。

生：图①被拉长了，图②被压扁了，只有图③没变形。

师：你们的感觉不错，的确只有图③才是数学意义上的放大。

本课的生长“原点”是学生学习过的图形的“平移与旋转”，学生有一定的活动经验。但小学生易把生活中图形的变大和数学意义上的放大混淆起来，这对新知学习会产生负面干扰。

在准确把握学生的认知水平和活动经验的基础上，教师通过动态演示，引导学生回顾复习图形的平移与旋转，继而直奔主题，既让学生感受到数学知识的系统性，又便于学生对知识进行有效的迁移和比较。借助电子白板，对图形进行水平拉、垂直拉、对角拉，是把握学生生长的“原点”，使学生初步感知生活中的“变大”与数学意义的“放大”是不同的，从而产生积极的学习心向。

二、生长课堂的撬动需要“支点”

数学课堂生长的“支点”是什么？数学核心素养最终的落脚点离不开问题的解决，好的问题能牵一发而动全身，可以成为生长课堂的“支点”。

【教学片段2】

师：现在，关于图形的放大和缩小，你有什么问题想问的吗？

生：图形的放大和缩小到底有什么规律？

生：为什么图形放大和缩小后大小变了，但形状不变？

生：到底怎样能把一个图形放大或缩小？

……

师：同学们都非常善于思考，提的问题很有价值。你们觉得图形大小变了、形状不变的原因是什么呢？（教师静静地等待）

生：我觉得与它们长和宽的比值有一定关系。

生：我也想知道它们的数据。

师：好！请你们借助方格图来研究（出示方格图），看看能发现什么。

（学生自主研究，小组交流分享）

生：我们小组发现原图的长与宽的比是3∶2，图③的长与宽的比也是3∶2，所以形状不变。

生：我们小组发现原图长与图③长的比是1∶2，宽的比也是1∶2。

师：同学们的研究非常有价值。你们的发现和书上一样吗？仔细读一读，琢磨琢磨哪个词特别重要。

把长方形的每条边放大到原来的2 倍，放大后的长方形与原来长方形对应边长的比是2∶1，就是把原来的长方形按2∶1的比放大。

生：我想提醒大家注意的是“每条边”，也就是长和宽要同时放大相同的倍数。

生：我认为“对应边长”也很重要。新图长与原图长的比是2∶1，新图宽与原图宽的比也是2∶1。

教师围绕教学目标一共提了三个核心问题，而每一个问题都具有开放性、思考性和生成性。第一个问题：关于图形的放大和缩小，你有什么问题想问的吗？让学生自己提出问题，不仅培养了学生的问题意识和主动思考的习惯，同时也激发了学生进一步探索的欲望。第二个问题：你们觉得图形大小变了、形状不变的原因是什么呢？请你们借助方格图来研究，看看能发现什么。给学生创造了一个较大的思维空间，让学生在自主探索、合作交流中发现图形放大和缩小的本质特征。第三个问题：仔细读一读，琢磨琢磨哪个词特别重要。引导学生对书本中的“每条边”“对应边长”等关键术语进行关注，使其应用到学生的表达中。

适度的“大问题”是撬动生长课堂的“支点”。

三、生长课堂应点化生长的“助力点”

尊重儿童的成长规律，遵循儿童的生长方式，教师要善于在教学中细致耐心地倾听、观察，及时捕捉有价值的生成点，有的放矢地进行“点化”，引发学生展开更深层次的思考和争辩，从而为学生的思维生长助力。

【教学片段3】

在“图形的放大和缩小”一课的巩固练习环节，教材安排了这样一道习题：

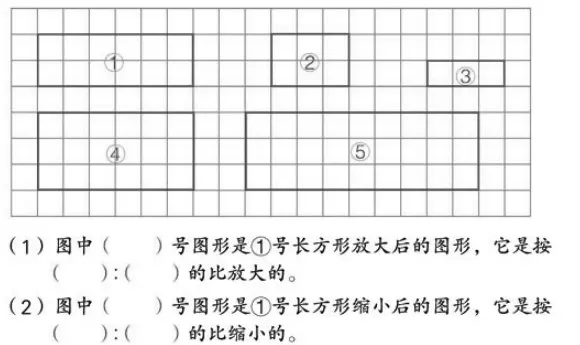
课件出示①号长方形，不出示方格背景和其他图形。

师：老师想考考你们的眼力。观察①号长方形，感觉一下。

（生静静地观察。停留了几秒钟，教师再出示另外四个长方形）

师：凭直觉，你觉得哪些图形是①号图形放大或缩小后的图形？

生：我感觉是⑤号。

生：我觉得是③号。

生：④号肯定不是，图形的放大和缩小必须是长和宽同时放大或缩小相同的倍数，④号的长和①号的长是相等的，而宽却相差很多。

（师继续演示课件：添上方格图）

师：赶紧验证一下，看看谁的猜测是正确的。

（学生静静地思考、计算）

生（兴奋）：确实是③号和⑤号。

师：恭喜你们！那现在你能完整地说说它们分别是①号长方形怎么变化来的吗？

生：⑤号图形是①号长方形放大后的图形，它是按3∶2的比放大的。

生：③号图形是①号长方形缩小后的图形，它是按2∶1的比缩小的。

生：不对！应该是按1∶2的比缩小的。

生：我有点混淆了。

师：你们有什么好办法区分图形是放大还是缩小？

生：我发现表示图形放大时，比的前项要大于后项，表示图形缩小时，比的前项要小于后项。

生：其实这也很好理解，因为比的前项表示新图的边长，后项表示原图对应的边长，所以前项大就是放大，前项小就是缩小。

师：发现了窍门！谁来当小老师，任意说一个比，考考大家是图形的放大还是缩小？

（学生互相考对方）

师：老师也来考考你们——1∶1。

生（边笑边答）：不变！

师：a∶b。

生：这个应该是无法确定的。

师：那你能具体地说一说吗？

生：如果a大于b，那就是放大，如果a小于b,那就是缩小，如果a等于b那就是不变。

师：真了不起，总结得简洁又全面！

（教室里顿时掌声四起）

教师把静止的教材习题作了动态呈现，培养了学生的直观洞察力。通过添上方格图，引导学生验证猜想，并让学生完整地说说它们分别是①号长方形怎么变化来的。当有学生把“按1∶2 的比缩小”说成“按2∶1 的比缩小”时，教师并没有就此罢休，而是紧紧抓住学生的“疑点”和“易错点”继续追问：“你们有什么好办法区分图形是放大还是缩小？”把学生思维的触角延伸到问题的深处。通过讨论交流，学生把握了图形放大和缩小的本质。最后在“谁来当小老师”环节，教师适时参与其中，引出“1∶1，a∶b……”教师有的放矢的点化，助力了生长课堂的开展。

四、生长课堂应着眼于生长的“远点”

学生在当下课堂学习中获得的进步，也是未来“远点”发展的基石。

【教学片段4】

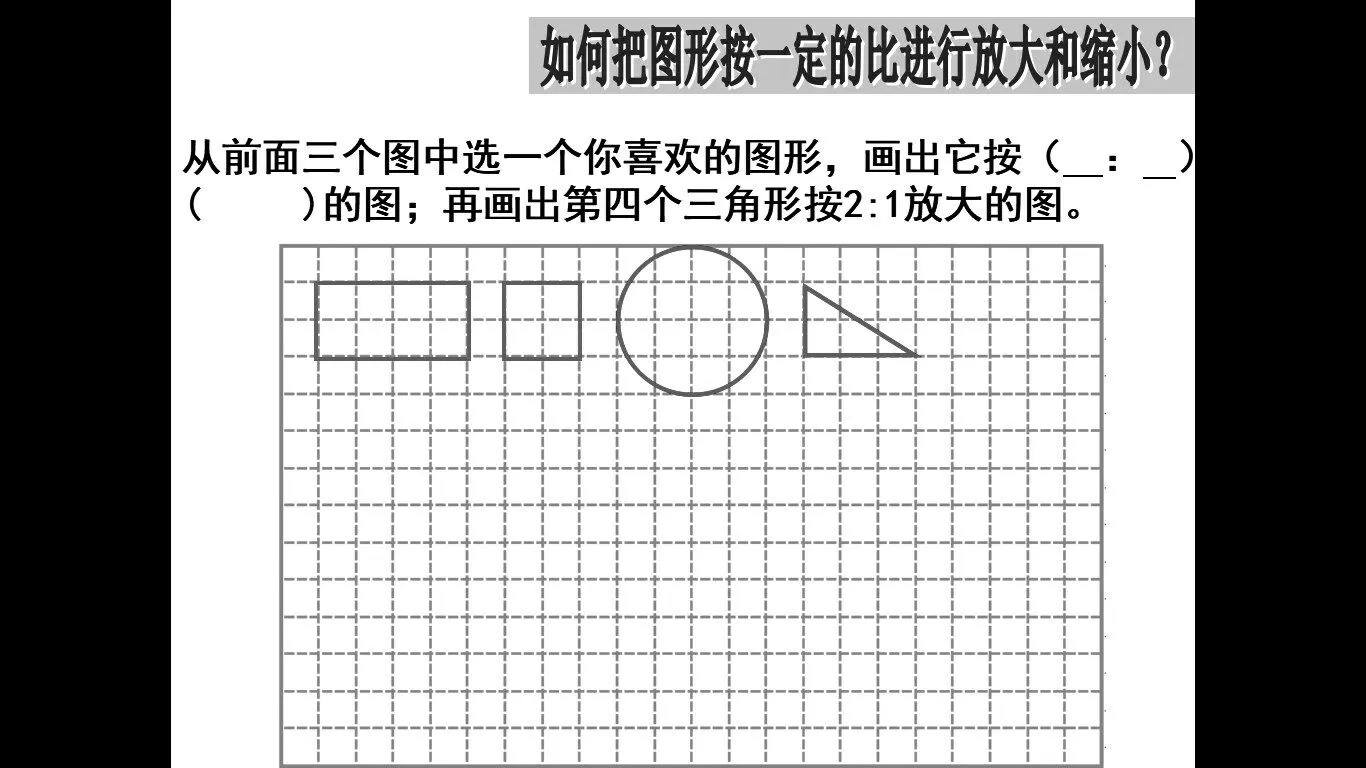
（1）请你从前面三幅图中选一幅进行研究，画出原图按（ ）∶（ ）的图。

（2）再画出第四个三角形按2∶1放大的图。

师：关于这几个图形的放大和缩小，小组交流后，大家还有问题或者建议吗？

生：我有个小建议，大家在选图形时，可以选简单点的，这样不容易错。

师：那你们觉得把哪个图形放大或缩小比较容易呢？说说理由。

生：我觉得把正方形放大和缩小最简单了。

生：我也同意。因为正方形只要确定它放大或缩小后的边长就可以了，不像长方形和圆那样麻烦。

生：我不同意，圆也很简单。因为决定圆大小的就是它的半径，所以只要确定圆放大或缩小后的半径就行了。

（学生恍然大悟地连连点头）

师：刚才，老师发现好几个小组对最后一个图形进行了讨论，是吗？

生：我们组的小A一开始怎么也画不好。他坚持要先放大斜边，又画不对。

师（转向小A）：如果重新让你画一次，现在你会怎么画？

生：只要先把这个三角形的两条直角边进行放大，再把斜边连起来。

师：那放大后的斜边与原图斜边有什么关系？

生：放大后的斜边也是原图斜边的2倍。

师：既然放大后斜边也是原来的2 倍，那你又联想到了什么呢？

（教室里顿时安静了下来，片刻过后，一双双小手陆续举了起来）

生：斜边上的高可能是对应高的2倍。

生：我觉得周长也可能是原来的2倍。

生：面积可能也是原来的2倍。

生：我不同意，面积不是原来的2倍，是原来的4倍。

……

师：大家有很多猜想，感兴趣的同学课后可以验证一下。不过我要特别表扬刚才这些同学，咱们学习数学就要有这样一种精神，善于联想，大胆猜想，这样才能让自己的思考往前迈进一步。

以上教学中，教师抓住学生出现的疑点、混淆点引导交流辨析，适时提出“既然放大后三角形的斜边也是原来的2倍，那你又联想到了什么呢”“放大后图形的周长会不会是原来的2 倍”“面积呢”“斜边上的高呢”，把学生的思维引向纵深处。教师的及时总结评价，对于培养学生的问题意识非常有意义，学生遇到问题时能在脑中多打几个问号，多问几个为什么，养成由此及彼联想的习惯，这些恰恰是学生为未来积蓄生长能量的良好学习品质。

从学生的原点到远点，需要教师为学生提供适宜的土壤，把握生长原点，遵循自主生长方式，引领学生通往生长的“远点”。