基于“整体把握”的初中数学章节起始课的教学设计

吴淑瑶

摘要：通过“整体把握”教材的兩个维度，对数学的核心知识及思想方法有清晰的认识；能重视了解学生的需求和教材的教学价值。在起始课的教学设计上重视整个章节的知识结构联系，使得学生在起始课学习的过程中获得明确的目标性、方向感，提高了学生起始课的兴趣和后继学生的主动性。

关键词：整体把握；初中数学；教学设计

中图分类号：G633.6文献标识码：A文章编号：1992-7711（2020）11-0151

浙江省特级教师朱先东指出：现行的数学教材基本按公理化的体系从下往上螺旋式展开，学生学习的是“点状”知识，虽然降低了学习的难度，但很难明白所学知识点在整个单元中的地位和作用，导致学生很难将学到的知识整合成为一个整体，学生知识信息提取困难、学习的迁移度较低，从而难以激发学习的兴趣和主动性。

针对教材现状，笔者认为可以通过以下两个切入点去“整体把握”整个教材的所有相关章节内容，并在“章节起始课”中进行教学演绎，符合心理学所说的第一印象效应。

一、“教学导入”要关注学生需求、教育价值

说明：学生学习的主动性，内在需求，价值驱动是最重要的，所以要以具体情境问题为载体的形式出现激发学生的学习欲望。

教学导入策略：章节内容运用前置法

起始课在“整体把握”整章教材内容和整个相关章节的教学内容之间的辩证关系时，发现现行教材几乎是到最后一节应用课，教育的价值才得到体现。但运用问题前置，要以学生已有起点出发设计应用问题。

案例：七上5.1一元一次方程

环节一：引入设计

问题1：国际标准篮球比赛场地的长是28米，整个场地占地面积为420平方米。问比赛场地的宽是多少？

问题2：标准篮板的长比宽多0.75米，整块篮板面积为1.89平方米。问篮板的长和宽分别是多少？

设计说明：运用问题1起点低，学生对长方形面积公式很熟悉。运用问题2本质上和问题1还是面积公式，但已知量和未知量互换了。算式学生列不出来了，列方程却很简单，于是学习方程的价值就体现出来了。

二、“教学内容”要关注核心知识，运用核心思想方法

说明：对于教学目标来讲，知识的理解、技能的内化、思想的体会是一种过程性的体验活动，藏在学生实际操作思考活动中的，需要教师引导。

1.起始概念教学策略

（1）宏观展示模块内知识——构建知识框架

环节二：合作学习（只列式不计算）

①某品牌一个篮球按8折销售售价为72元，设这个篮球的原价为X元，可列出方程

②小强买3个篮球，老板一共优惠了8元，实际付了160元。设这个篮球的原价为X元，可列出方程。

③小强，小杰，张明进行投篮比赛，每人投20次。小强投进10个球，小杰比张明多投进2个，三人平均每人投进14个球。问小杰和张明各投进多少个？

师：怎么列方程呢？（教师特意不给定未知数，以后学生解决问题是要自己设未知数）

生：可设张明投进x个，列方程；可设小杰投进x个，列方程；可设张明投进x个，小杰投进y个，列出两个方程。

设计说明：多情境展示初中学习中的三种整式方程（一元二次方程，一元一次方程，二元一次方程），让学生对整式方程的框架有整体上的感悟，知道设不同的未知数可以得到不同的方程，为知识深化做好辅垫。

（2）分类归纳定义新概念——观察知识核心要素中，深化知识的理解

环节三：请你来找茬，给下列方程分分类

师：我们把环节二中列出来的方程都汇聚一起，老师再送你两个。请你来找茬，哪些方程和其他方程不太一样？为什么？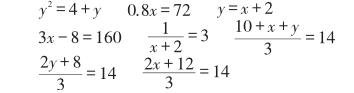

找茬是人的天性，学生很快观察出分式方程，一元二次方程，二元一次方程与其他方程的不同之处。

师：其他的4个方程又有什么共同点呢？你能根据它们的共性给它们下定义吗？

设计说明：延续环节二学生自己列的方程，进一步构建了完整的知识框架的同时在分类、归纳、类比中完成了新知识的深化理解并进行定义。这是发现式学习常常采用的思想方法。在上一环节，笔者的目的让学生见到模块中所有方程，这个环节才是真正理解与掌握所有方程的概念，知识框架稳扎在学生头脑中。

笔者还发现，当学生有了整体的感悟，在第一节课看过这些方程，学生学习后继新章节新方程完全不会有陌生感和惧怕心理，很快会融入学习。

2.后继概念与技能教学策略

（1）类比发现，求同存异定义新概念——理解知识的形成过程

后继概念可参考起始概念类比教学。

案例：七下2.1二元一次方程

环节二：这两个方程有什么共同特点？请类比一元一次方程给它们下定义。

0.6x+0.8y=4.8，2a=3b+20

（2）类比探究，新旧异点，明确转化方向——培养问题解决的化归思想

案例：九下3.1直线与圆的位置关系

探究二：直线与圆的位置关系还能怎样定？

①点和圆有几种位置关系？怎么判定？

②能否通过直线上某一点与圆的位置关系来判定直线与圆的位置关系？

设计说明：在与圆相关的章节知识中，点与圆的位置关系是已有知识，研究过程与方法基本相同，但是不同的是点变成直线。学生只有发现这一点，才能把新问题转化为如何在直线上找一个特殊的点来运用已有的知识解决问题。

三、“章节起始课”整体把握策略的成效

笔者发现，在章节起始课上努力给学生构建一个前后一致、逻辑连贯的学习过程，一个知识体系完整的框架图。让学生对整个单元的学习内容有初步的整体感悟，给学生展示一张完整的“森林”导图，学生完全可以从自身个性出发，依据自身对知识框图的认识，思考问题的切入点，处理的方式和方法，更能据此提出新的问题。学生带着起始课的目标和产生的问题自然而然地进入后继课节的讨论层面。这样就弥补了教材的编排和相应的传统章节教学过程的不足。

参考文献：

[1]朱先东.例谈数学整体性教学设计的策略[J].中国数学教育：初中版，2012（7）.

[2]章建跃.从数学整体观看“同底数幂的乘法”的教学》[J].中国数学教育：初中版，2013（7）.

[3]牟录贵.数学教学中整体观念的培养——兼谈数学教学改革[J].甘肃高师学报，1999（5）.

（作者单位：浙江省温州市鹿城实验中学325000）