从相遇问题的直观解释谈数形结合

郭家兵

[摘要]数形结合是小学数学常用的数学思想方法。教学中从以形析题、以形助题、由形到数三个方面去应用，能使问题变得直观形象。尤其是在相遇问题中，运用数形结合方法，能清楚、快速地建立等量关系，可提高解题的速度与效率。

[关键词]相遇问题;数形结合;画图

[中图分类号]G623.5 [文献标识码]A [文章编号]1007-9068（2020）08-0023-02

数形结合既是一种重要的思想方法，又是解决问题的有效方法。数形结合就是把抽象难懂的数学语言、数量关系与直观形象的几何图形结合起来，使抽象问题具体化、复杂问题简单化。

两个物体从两地出发，相向而行，经过一段时间，必然会在途中相遇，这类题型称为相遇问题，其研究的是速度、时间和路程三者之间的数量关系。相遇问题对学生而言是一大难题，其实解决相遇问题的最佳方法是借助直观图例，数形结合予以分析。

一、以形析题

用方程求相遇时间的问题出现于人教版教材五年级上册第五单元。题目以主题图的形式予以呈现，题目有对话、有叙述的条件，要求学生全面分析并理解。由于题目中的条件过于复杂，学生可以通过以形析题，把题目的条件用线段图逐步细化，方便直观地对数量关系进行判断，把复杂的数量关系变得形象和具体。

师：现在是上午9时，仔细观察，这两位同学同时出发，他们是怎么走的？

（课件动态演示）

师：这样面对面地走，在数学上称为相向而行。

师：经过多久两人相遇？

（先用小问题将大问题细化，便于学生精准把握有效的解题信息）

师：谁能试着用自己的话完整地说一说下面这幅图的意思？

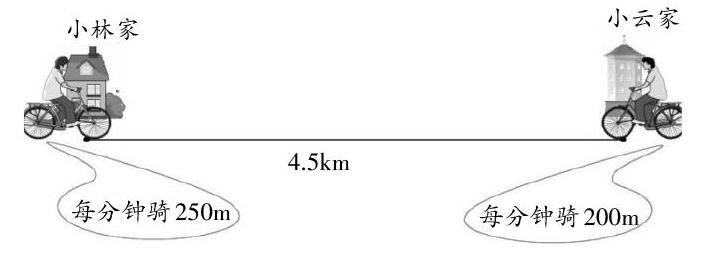
生1：小林家和小云家相距4.5千米。一天上午9时，两人分别从家骑自行车相向而行，小林每分钟骑250米，小云每分钟骑200米，经过多少分钟两人相遇？

师：用线段图直观演示一下题目的意思。

师：假设小林从出发到与小云相遇花了3分钟，那么小云从出发到与小林相遇用了几分钟？

师：他们两人从出发到相遇，所经过的时间怎么样？（相同）

师：也就是说两人相遇时经过的时间相同，这个时间就称为相遇时间。今天，我们就来研究与相遇时间有关的相遇问题。

以形析题，可促进学生更好地理解知识点。教师在平时的教学中一定要培养学生运用数形结合方法解题的习惯，引导学生学会画简单的线段图分析问题，如行程问题、分数应用题等。

二、以形助题

对于上述相遇问题，用方程法求相遇时间有两种最基本的等量关系式：小林骑的路程+小云骑的路程=总路程，小林、小云每分钟骑的路程之和×相遇时问=总路程。怎么让学生理解这两个等量关系式呢？可以借助数形结合，以形助题，将抽象的关系式变成形象的图形，降低问题的难度。

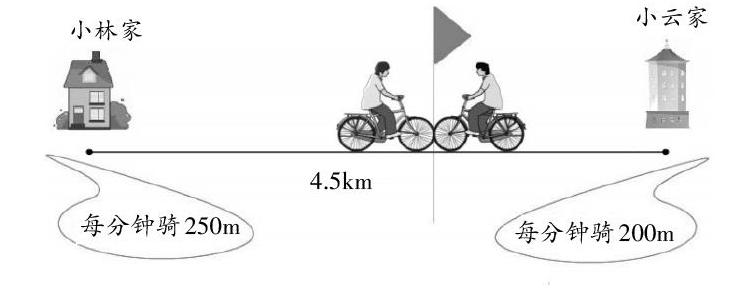
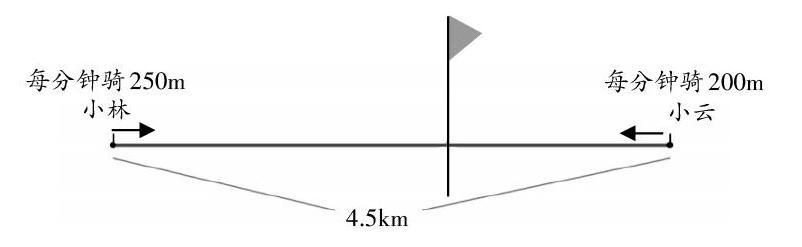
师：请观察线段图，旗子左边是小林骑的路程，右边是小云骑的路程，把这两部分合在一起是什么？

师：你能根据线段图列出方程嗎？

生2：250x+200x=4500。

师：250x表示什么意思？200x又表示什么意思？为什么要加起来？

生3：两人各自骑的路程合起来就是总路程。

师（出示关系式：小林骑的路程+小云骑的路程=总路程）：要想知道x=10对不对，该如何检验？

数与形是数学教学研究对象的两个侧面，用图形研究数量关系，并分析问题、解决问题，这就是以形助题。

师：谁还有不同的解决方法？

（出示“小林、小云每分钟骑的路程之和×相遇时间=总路程”，课件动态呈现）

师：两人同时出发，骑了1分钟，①是小林1分钟骑的路程，②是小云1分钟骑的路程。

师：将这两条线段合在一起代表的是什么？（两人1分钟骑的路程之和，也就是每分钟骑的路程之和）

师：继续骑，又骑了1分钟，现在一共骑了几分钟？他们2分钟骑的路程之和怎么求？

生4：小林、小云每分钟骑的路程之和×2。

师：继续骑，又骑了1分钟，现在一共骑了3分钟，他们3分钟骑的路程之和又怎么求？生5：小林、小云每分钟骑的路程之和×3。

师：一直骑，直到相遇，所骑的时间就是他们的相遇时间，每分钟骑的路程之和×相遇时间=总路程。

师：现在谁能根据这个关系式列出方程？

生6：（250+200）x=4500。

师：求出x=10说明什么？（10分钟时两人相遇）

师：如果现在问题变成“两人什么时候相遇”，怎么解决？

（板书：9时+10分=9时10分）

师：这个等量关系式你明白了吗？谁把这个关系式再说一遍？

师：同学们，我们用了两个不同的方程来解决这道题，请你对比这两个方程，有什么不同？

（等量关系式不同列的方程就不同）

每分钟骑的路程之和×相遇时间=总路程，这一等量关系式的理解对学生而言比较难。以形助题时，对于比较难懂的知识点，教师要充分利用多媒体技术进行动态演示，充分丰富“形”，以便学生理解。要突破等量关系式这一难点，可以动态地分层次呈现线段示意图，以此沟通数学知识之间的联系，从复杂的数量关系中凸显最本质的特征，提炼出等量关系“每分钟骑的路程之和×相遇时间=总路程”，既解决了问题，又促进了学生形象思维和抽象思维的协调发展。

三、由形到数

“形”的介入，只是一种问题解决的策略，能使问题得以巧妙解决。先形后数的数学教学遵循了学生的心理发展特性。在此基础上，教师还要通过一定的练习，让学生对数学问题的解决策略得到强化，对数学本质的理解得到提升。

师：下面2道题，只列方程，不计算。

1.甲、乙两个工程队共同开凿一条570米长的隧道，各从一端相向施工。甲工程队每天开凿110米，乙工程队每天开凿80米，经过几天完成任务？

2.师傅和徒弟两人同时开工，共同加工1200个零件，师傅每小时加工300个，徒弟每小时加工200个，几小时能完成任务？

师：今天学习的这3道题目有什么相同点？请4人一组，相互说说自己的想法。

师：这3道题都是求“相遇时间”，都可以用线段图来表示。

小结：线段③、④分别表示甲、乙要共同完成的工作（走的路程），甲与乙都是同时开工（相向而行），最后完成总工作（相遇）。线段③表示甲的工作量，线段④表示乙的工作量，合起来就是共同完成的总工作量，或者用甲、乙1小时、1分钟、1秒，即单位时间工作量的和乘相遇时间得到工作总量。这些都可以称为相遇问题。

本文最后把行程问题、工程问题、工作问题用线段图的形式汇总，通过由数到形再由形到数，将抽象问题转变成统一的图形问题，然后予以归纳提升。这种数与形的有机契合，方便学生直观地对数量关系进行判断，把复杂的数量关系变得形象和具体，既有利于学生迅速寻找到解题方法，又可有效提升课堂教学效果，更能实现学生数学思想的升华。

我国著名数学家华罗庚先生曾经说过：“数形结合百般好，隔离分家万事休。”教师要着眼于每个教学细节，最大限度地将数形结合思想渗入课堂教学过程中，把数形结合的功效发挥出来，这样不仅有利于学生更好地掌握数学知识，而且能培养学生的学习兴趣，锻炼他们的逻辑思维能力，为学生今后的发展打下坚实的基础。

（责编：吴美玲）