站在门槛外看微积分
阚尚锦

[摘要]极限思想是近代数学的一种重要思想。通过教学内容、教学设计和知识联系三个角度研究如何在小学数学课堂教学中渗透极限思想。
[关键词]极限思想;数学思想;微积分
[中图分类号]G623.5 [文献标识码]A [文章编号]1007-9068(2020)08-0008-02
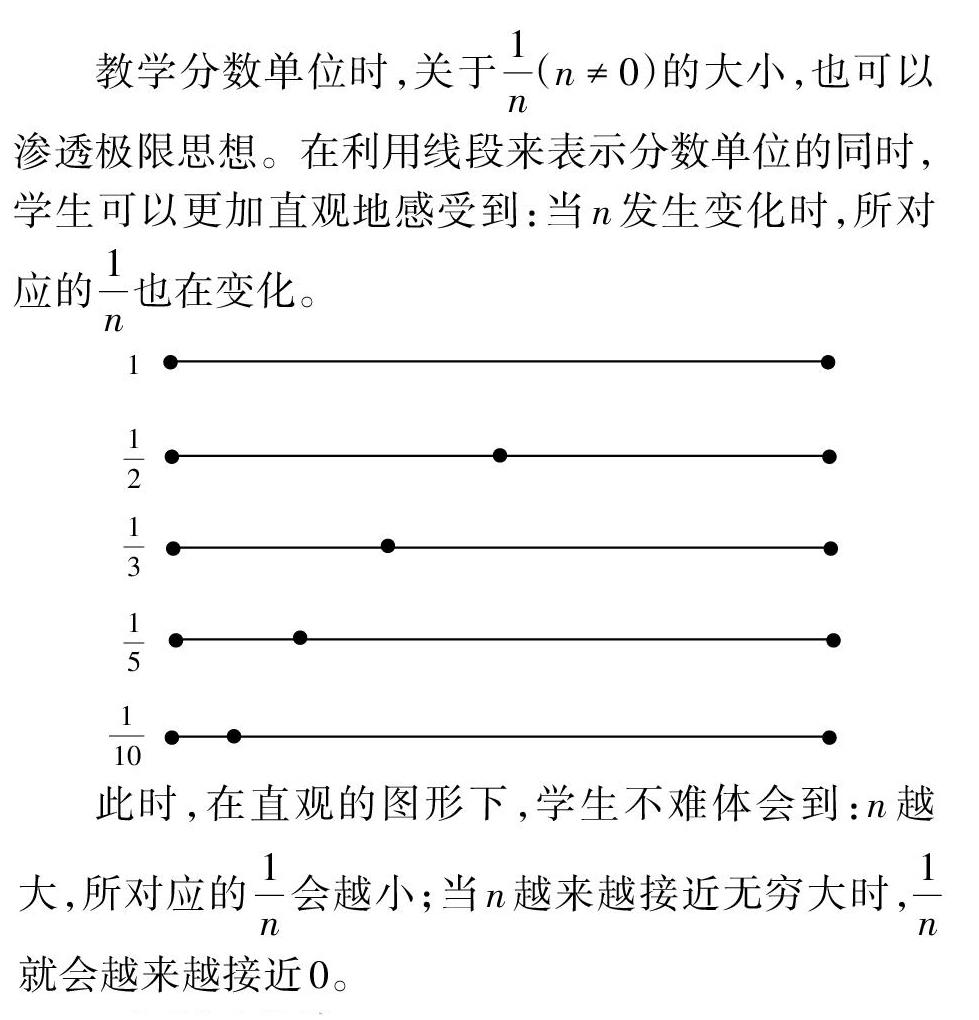
极限思想是近代数学的一种重要思想,是指用极限概念分析问题和解决问题的一种数学思想。在小学阶段,想要渗透这种思想,教师需要给学生搭建探究发现的平台,给学生提供有效的“支撑”和充分的探索实践机会。这样学生才能切身体会到无穷的奥秘,感受极限的思想。本文将结合教学实例,谈一谈如何在小学数学教学中渗透微积分的理论基础——极限思想。
一、“看”教学内容。渗透极限思想
小学数学教材中的很多内容都适合渗透极限思想,只要选用恰当的方法,就能让学生在学习探究的过程中体会无限和无穷的意义,并利用对极限思想的感知,归纳总结出新知。
1.“数”的教学
教学自然数、奇数和偶数时,就可以让学生感受:只要没有范围的限制,自然数是数不完的,奇数和偶数是有无穷多个的,因为没有最大的自然数,也没有最大的奇数和偶数。
教学无限小数时,对于1÷6=0.166...,学生一开始会纠结于除法算式除不尽,除不尽的含义就是除不完,如果要将这个算式的得数一直写下去,那小数点后的数字是写不完的。
2.“形”的教学
教学直线和射线时,想要学生清楚它们和线段的区别,可让学生闭着眼睛想象:直线和射线都是无限长的,它们可以一直延伸下去,无边无际,但直线是两端无限延长,没有起点也没有终点的,而射线是一端固定,另一端无限延长,是有起点无终点的。只有弄清楚了这三种线各自的特点,才能真正洞悉它们的数学本质。
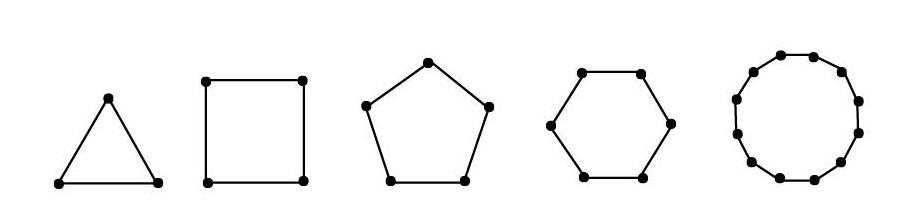
教学“正多边形”时,教师常常会在教学正三角形和正四边形的特征之后加入正五边形、正六边形,让学生观察正多边形随着边数的增加所发生的变化。
通过图形,学生很快就能发现,随着边数的增加,正多边形会越来越接近圆,那当边数无穷大时,正多边形是否就成为圆?在你一言我一语的表达中,学生经历了一场头脑风暴,极限思想也在学生的脑中生根。这样的学习让学生感受到了极限思想的精髓,打破了学生思维定式中“直”与“曲”的界限,在无穷中实现了变直为曲,有利于学生走出有限的几何观念,形成无限的几何观念。
要想在课堂教学中渗透极限思想,就要选择合适的教学内容和方法,这样才能做到“润物细无声”,使得学生在探究新知的过程中感知极限思想的价值。
二、“看”教学设计。加深思想感知
小学阶段的一些数学公式推导的教学常常需要渗透极限思想,以便学生更好地理解公式推导的过程。以“圆面积”这一课为例,在推导出圆面积公式之前,需要让学生感受两次极限思想。
1.“蜻蜓点水”,初步渗透
本节课需要解决课本上的两道例题,例1的教学目标是让学生利用数方格的方法来初步感知圆面积和r2之间是三倍多一些的关系。于是我设置了两个维度。第一维度是给出课本上半径分别为3、4、5的圆形,让学生通过数一数、算一算的方法,感受圆面积和半径的关系。学生大都能够发现圆面积和r2之间有着三倍多一些的关系,但具体的数据并不能由此而得到。因此,基于教材中的图形,我又增加了半径为8和半径为20的两个圆形。
通过原有的三个图形,学生能感受到圆面积和r2的大概关系,但增加了两个半径较大的圆形后,学生能够更加清晰地感受到,当半径变大时,圆面积与r2的关系更加接近π。在此基础上,我再追问:“如果这个圆无限大呢?”一石激起千层浪,学生的思维再一次被点燃,短暂的思维碰撞之后,学生提出S=πr2的猜想。在这过程中,学生能够感觉到无限大的这个圆其实就是一种极限的情况,体验到极限思想的无穷魅力。
2.“下马看花”,再次感悟
让学生带着猜想学习本节课的第二个例题,即圆面积公式的推导。推导圆面积公式一般有两种方法:刘徽的割圆术和教材中的将圆分割后拼接成长方形的方法。这两种方法都要求学生有极限思想。在教学中,为了让学生充分感知这两种方法,我发给每一位学生一张圆形纸片,让学生通过折一折、剪一剪、拼一拼的方法来自主研究圆面积的公式。在充分的动手操作后,两种方法都出现了。关于刘徽的“割圆术”,学生是这样呈现的:
从图中不难看出,随着圆内接正多边形边数的不断增加,正多边形的面积就越接近圆的面积,当正多边形的边数无限多时,正多边形的面积就是圆的面积,从量变转为质变。虽然小学生还无法解决正多边形面积的极限问题,但是这样的过程还是应该完整而清晰地展现给他们。学生会在你一言我一语的激烈交流和教师的讲解中拥有极限思想,理解无限逼近的动态过程。
关于教材中的方法,学生通过剪拼,可以得到一个趋近于平行四边形的图形:
学生在交流后也发现,当分割的份数变多时,拼接得到的图形会越来越趋近一个平行四边形。为了能让学生直观感受到极限的情况,我还利用了几何画板这一现代化工具来呈现趋近于极限时的画面。
【教学片段】
师:看了这样的一个动态过程,圆被这样平均分成很多很多份后,你认为能拼成什么?
生:长方形。因为分割得越多,拼接出的平行四边形左右两侧的斜度越大,如果分割成无限份,其左右两边就和上下的这两条边垂直,也就变成长方形了。
学生的回答赢得了热烈的掌声,可见学生已经真正理解了圆面积公式的推导过程和本质内涵。
以上关于圆面积公式的推导过程,采用了“化圆为方”“变曲为直”的极限分割思想。要想在课堂教学中渗透极限思想,教师需要在把握教材的基础上,给学生提供探究的平台和思考的扶手,让学生在一次又一次的感知中升华对数学思想的感悟。
三、“看”知识联系。深研数学本质
教师可在复习的时候利用數学思想引导学生打破知识的局限。例如,复习梯形面积公式和三角形面积公式时,就可以利用极限思想引导学生发现这两个公式之间的联系。梯形的面积公式是“(上底+下底)×高÷2”,而梯形的上底慢慢缩小直到缩小至一个点后,梯形变成了三角形,这个上底也变成了0,正好可以得到三角形的面积公式“底×高÷2”。
同样,可以引导学生利用这样的思想方法去思考正方形、长方形、平行四边形的面积公式。极限思想在这里正好能将平面图形面积公式的推导本质呈现给学生,让学生深刻感受到数学中的变与不变:变化的是表层特征,而核心的本质是不变的。
极限思想在小学生数学必备品格之数学思想中占有一席之地,是高等数学中微积分的基础。小学是学生形象思维向抽象思维转化的阶段,教师可以通过选取恰当的教学素材和创造进阶型教学设计这两个方面来帮助学生将极限思想一步一步植入到脑海中。这样的教学,留下的不仅仅是数学知识,更是一种数学素养,就像是我们带着学生站在门槛外看看微积分。
(责编:金铃)

