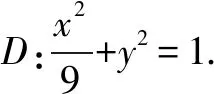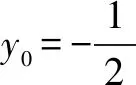从题目隐含信息中寻求解法的优化、简化及准确化
雷亚庆
(江苏省南京市大厂高级中学 210044)
我们在解决有些数学问题时,会碰到这样一种情况:一个问题如果按照常规思路很难去解决,即使能解决,也要大费一番周折,非常繁琐.而这时我们如果能根据问题的结构特征及其已知条件中的数量关系,挖掘潜在的已知和未知间的信息,通过巧妙的构造,就可以把问题转化为我们熟知的问题,从而使解答巧妙、简捷、准确.以下是笔者的一些粗浅的体会.
一、挖掘隐含信息,使解法得以优化
例1 求sin238°+sin282°-sin38°sin82°的值.
分析如果利用三角公式进行化简和求值运算,需要降幂公式和和差化积公式,仔细观察所给角的特征,我们发现隐含信息:38°,82°与60°正好构成一个三角形的三个内角,因此考虑构造三角形利用正余弦定理求解.
解构造△ABC,使得A=38°,B=82°,C=60°,设△ABC外接圆直径为2R,则:sin238°+sin282°-sin38°sin82°=sin2A+sin2B-2sinAsinBcosC
由正弦定理:sin2A+sin2B-2sinAsinBcosC
例2已知直线l:(2+m)x+(2m-1)y-3m-1=0,和圆C:x2+y2-x-y-2=0,试判断直线l与圆C的位置关系.
分析本题的常规思路有两种:一利用圆心到直线距离与半径的大小关系;二是联立方程组,消元后利用根的判别式判断方程解的情况进而得到直线域圆的位置关系.但是两种方法都面临复杂的运算与化简.这时如果换个角度审题,我们就会发现题目中隐含的重要信息,那就是直线过定点,只要判断定点与圆的位置关系就可以顺利解决本题.
解直线l:(2+m)x+(2m-1)y-3m-1=0的方程可化为
2x-y-1+m(x+2y-3)=0.



所以点A在圆C内.
所以过点A的直线l一定与圆C相交.
二、挖掘隐含信息, 使解法得以简化

常规解法分类讨论



(2)当1≤m (3)当m<1 综上,存在m=-2,n=0,使得f(x)的定义域和值域分别是[m,n]和[2m,2n]. 解得m=-2,n=0. 例4 集合A={x|x2+2x-3>0},B={x|x2-2ax-1≤0,a>0),若A∩B中有且只有一个整数,求a的取值范围. 分析如果我们设f(x)=x2-2ax-1,题目中包含两个隐含信息:一是对称轴x=a(a>0),二是f(0)=-1<0.由对称性可知x1<0 解A={x|x<-3或x>1},由题意B≠∅,f(0)=-1<0可知函数f(x)=x2-2ax-1有两个零点,不妨设为x1,x2(x1 因为抛物线f(x)=x2-2ax-1的对称轴为x=a(a>0), 由对称性可知x1<0 若x1<-3,则x2>3,则A∩B={x|x1≤x<-3或1 因此若要A∩B中有且只有一个整数,需2≤x2<3,此时A∩B={2}(如图1),所以f(2)≤0且f(3)>0(如图2). 例5 已知3x2+2y2=6x,试求x2+y2的最大值. 正解由3x2+2y2=6x得 错因只考虑了B是锐角,忽视了隐含信息:A和C也是锐角,导致B的范围不精确. 分析这是一个二元目标函数的最值问题,从代数角度很难找到解题思路.这时我们仔细观察目标函数的特征,就会发现隐含的解题信息:二元目标函数可以转化为两条特殊曲线上的两个动点间的距离,解题思路由此清晰. 问题转化为:求椭圆D上一动点Q到圆C上一动点P的距离的最大值 显然当PQ过圆C的圆心C时才可能取得最大值,即PQmax=PCmax+1 由此问题进一步转换为求定点C(0,4)与椭圆上动点Q的最大距离问题 分析求根式函数的值域是一个难点,特别是双根式函数,实际上如果我们养成解决函数问题先明确定义域的好习惯的话,就会发现隐藏的解题信息,利用三角代换,就可以把根式函数转换为三角函数问题处理. 例9 (浙江2015文 )若实数x,y满足x2+y2≤1,则|2x+y-4|+|6-x-3y|的最大值是____. 分析习题咋一看很难,目标函数是一个二元双绝对值函数,如何才能去绝对值呢?怎么分类讨论呢?有点无从下手的感觉,实际上如果我们根据题干中隐含的信息作出可行域,就会发现原来问题比想象的简单的多. 解析作出x2+y2≤1对应的区域,同时作出直线2x+y-4=0和直线x+3y-6=0(如右图).由图形结合线性规划的知识可知: x2+y2≤1对应的区域内的任意一点(x,y)都满足线性约束条件:2x+y-4<0且x+3y-6<0, 所以有:z=|2x+y-4|+|6-x-3y|=4-2x-y+6-x-3y=10-(3x+4y). 问题转化为:若实数x,y满足x2+y2≤1,求目标函数z=10-(3x+4y)的最大值. 因为x2+y2≤1, 所以可设x=rcosθ,y=rsinθ(r≤1). 所以z=10-(3x+4y)的最大值为15,故|2x+y-4|+|6-x-3y|的最大值为15. 从上述问题的解决过程中我们发现:解题时,要注意审题,不仅能从表面形式上发现特点,而且还能从已知的相关量进行定量分析,充分挖掘题目中的隐含信息,从中寻求解题思路的优化、简化、准确化乃至解题方向,避免无谓的分类讨论或繁琐的运算化简,提高思维的变通性,使问题得以顺利解决.

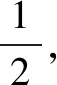


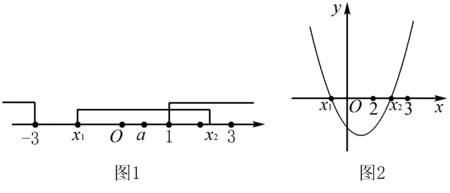
三、挖掘隐含信息,使解题方法准确化







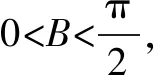


四、挖掘隐含信息,使解题思路清晰化