关注圆的形成 加强解题应用

陈志年

(安徽省合肥市肥西中学 231200)

圆是我们大家很熟悉的一种图形，看似简单，实则奇妙，奇妙得连它的形成方式也多种多样.下面就圆的三种简单形成方式，例析它在解题中的应用.

一、圆的第一种形成方式

平面内到定点的距离等于定长的点的轨迹是圆.这是大家熟悉的圆的定义，也称为圆的第一定义.

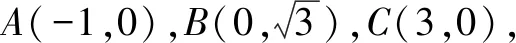
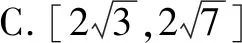
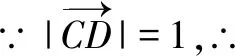
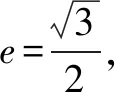
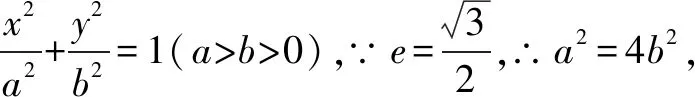
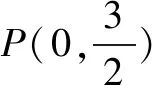
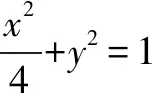
二、圆的第二种形成方式

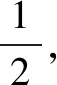
推广：平面内到两定点A,B的距离之比为正数λ(λ≠1)的点的轨迹是圆.与椭圆、双曲线的第二定义类似,我们把“平面内到两个定点的距离之比为正数λ(λ≠1)的点的轨迹是圆”叫作圆的第二定义.

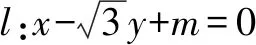
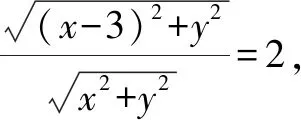
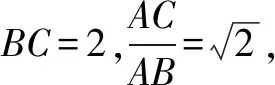
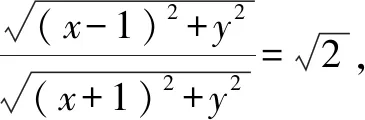
三、圆的第三种形成方式

平面内对定线段所张的角为θ(θ为常数且0<θ<π)或它的补角π-θ的动点轨迹是圆(除去线段两端点).

例5(智学网试题改编 )在△ABC中，角A，B，C的对边分别为a，b，c，已知向量m=(cosA,cosB),n=(a,2c-b)且m∥n.

(1)求角A的大小；

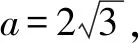
解(1)∵m∥n.

∴acosB-(2c-b)cosA=0.

在△ABC中，acosB+bcosA=c,

∴c-2ccosA=0,

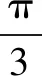
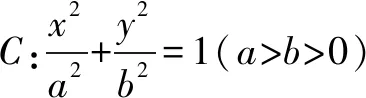
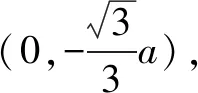
以上各例我们是通过关注圆的三种形成方式，明确点在圆上，通过圆的方程或图形解决了问题；可见，增强意识，适时而用，切入解题，简化思维过程，收到很好的效果.