基于2019年高考下的导数压轴题探究

张丽群 指导教师：林为华

(福建省莆田擢英中学 351100)

一、恒成立、存在性含参问题

此类题，是高考导数压轴题中较为常规的一种.分离参数后，加入一次导或者二次导的二次函数分类讨论，转化成去求新构造函数最值的问题.类比，这种思路也适合与导数和三角函数结合的含参数的问题处理.在此类题中，若出现不定型的导函数，那我们还可以对一些层次较好的同学传授一些大学中对于不定型导函数的处理方法，例如洛必达法则的应用.当然，最好进行分类讨论，虽然运算较为繁冗.

例如下面这道题目：考查了利用导数研究函数的单调性,零点等问题,和数形结合的思想方法,难度较大．

(1)令g(x)=f′(x),对g(x)再求导,研究其在(0,π)上的单调性,结合极值点和端点值不难证明；

(2)利用(1)的结论,可设f′(x)的零点为x0,并结合f′(x)的正负分析得到f(x)的情况,作出图示,得出结论．

例题1已知函数f(x)=2sinx-xcosx-x,f′(x)为f(x)的导数．

(1)证明：f′(x)在区间(0,π)存在唯一零点；

(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围．

解(1)可求得f′(x)=2cosx-cosx+xsinx-1=cosx+xsinx-1.令g(x)=cosx+xsinx-1,则g′(x)=-sinx+sinx+xcosx=xcosx.

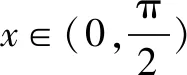
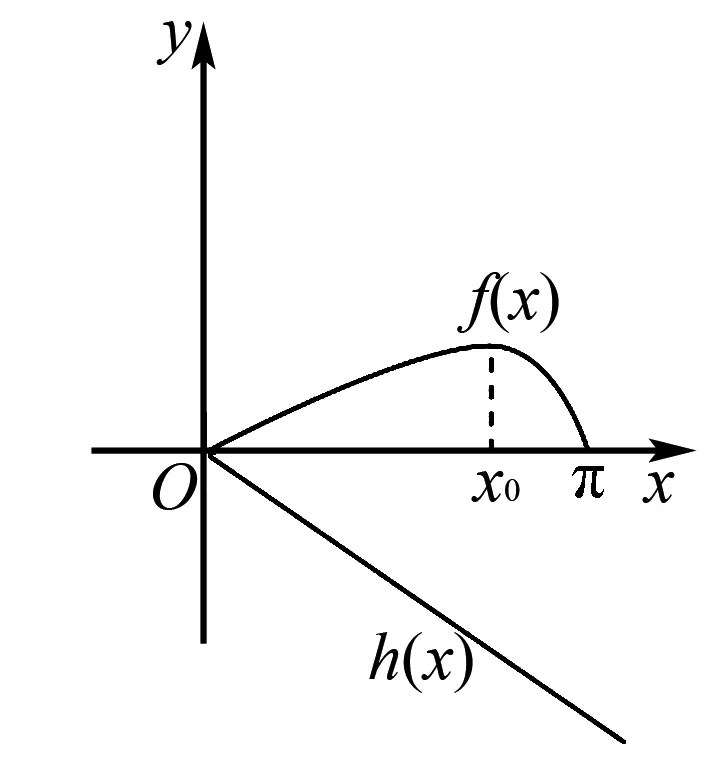
(2)方法一

由(1)知,令h(x)=ax,作出图示,∵f(x)≥h(x),

∴a≤0．

方法二令h(x)=f(x)-ax=2sinx-xcosx-(a+1)x,则h′(x)=cosx+xsinx-1-a,令m(x)=cosx+xsinx-1-a,m′(x)=xcosx=g′(x).

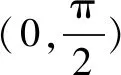
①当a≤-2时，h′(x)min=h′(π)=-2-a≥0，即h′(x)≥0在[0,π]上恒成立，∴h(x)在[0,π]上单调递增，h(x)≥h(0)=0,即f(x)≥ax,此时f(x)≥ax恒成立.

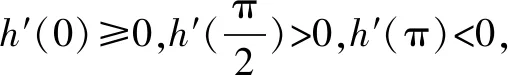
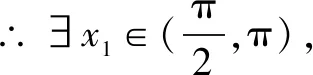
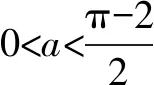
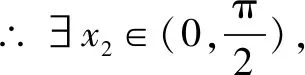
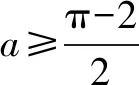
综上所述：a∈(-∞,0].

二、导数中“对称直线”的妙用

对较复杂含参的函数，先分离参数，构造一个新的函数，若运算量很大的话，那我们就要思考，能不能将问题等价转化，并实施转化分解变形.在考虑零点方面的问题，一般还要转化成两个函数来求交点的问题.而且，在导函数的小题压轴题当中，我们还会遇到，转化后，两个函数图象是关于某一条直线对称的，或者是某一条曲线的切线等情况.那这条直线的存在就为我们提供了非常好的几何法方面的思路.我们试着找到这一条直线，然后将题目转化成两个差函数来求解，问题就很快地得到处理.

例题2已知函数f(x)=e1-x(-a+cosx),a∈R.

(1)若函数f(x)存在单调增区间,求实数a的取值范围；

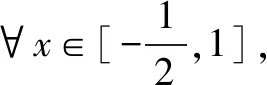
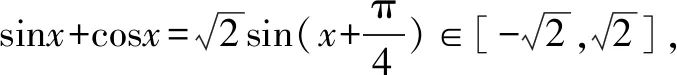
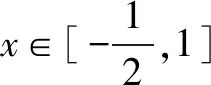
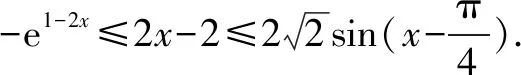
评析(1)函数f(x)存在单调增区间,所以方程f′(x)>0有解,即可求实数a的取值范围；

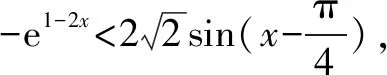
三、导数中的“隐零点”

导数中，最近热门的话题，非隐零点不可了.圆锥篇章，我们就已经接触“设而不求”跟韦达定理的完美展示.那在导数这边，更是把这种思想发挥得淋漓尽致.利用导函数的零点作为解题桥梁，设出零点，用零点来换元或者消元，从而转化成我们学过的简单函数来进行求解.比如以下这道题目：本题考查导数的运用：求极值和单调区间,主要考查三角函数的导数和求值,同时考查等比数列的定义和通项公式的运用,考查不等式恒成立问题的证明,属于难题．

例题3已知函数f(x)=eaxsinx(x∈[0,+∞))，a>0.记xn为f(x)的从小到大的第n(n∈N*)个极值点.

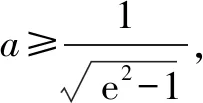
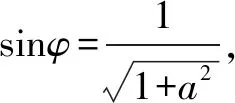
四、导数中巧用不等式性质

近几年的高考中，压轴题时常出现与不等式知识点交汇的题目.但是加入三角函数不等式的导数问题，还是比较新颖的，具有一定的解题难度.我们可以利用绝对值不等式、三角不等式等，来进行解题.比如以下这道题目：本题主要考查函数的导数以及函数最值的应用,求函数的导数,利用函数单调性和导数的关系,以及换元法,转化法，转化为一元二次函数是解决本题的关键.综合性较强,难度较大．

例题5设函数f(x)=acos2x+(a-1)(cosx+1),其中a>0,记|f(x)|的最大值为A．

证明：|f′(x)|≤2A．

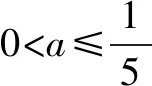
综上：|f′(x)|≤2A．