千举万变 其道一也——一道北京高考题的改编探讨

程春暖

(北京市实验学校(海淀) 100037)

函数是高中数学课程内容的主线，是学生进入高中之后接触到的第一个难点，也是让许多学生望而生畏的数学概念.从初中的注重直观到高中的逐步抽象，学生对函数的认识在理论上应当上升了一个层次.但实际上，许多学生还是：

看到函数，慌了；

没有头绪，乱了；

陷于计算，凉了；

再有参数，完了.

本文以一道分段函数的单调性问题为背景，通过对题目的改编，以求让学生体会解决函数问题关注其图象与性质才是关键.

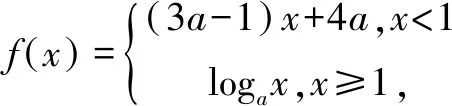
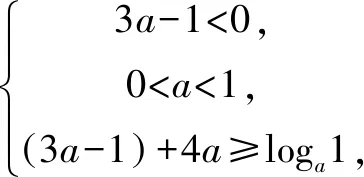
改编角度1 单调性的定义

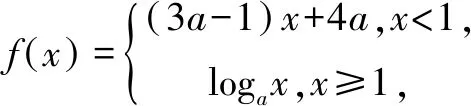
本练习在原题的基础上考查了函数单调性的定义.作为第一种变形，知识跨度较小，易于理解，学生接受度也较高.

改编角度2 单调性与零点的关系

零点是函数的重要性质，零点个数与函数的单调性之间有密切关系，因此将问题定位在零点个数考查单调性也是一种常见的方式.

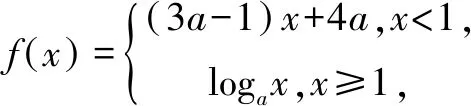
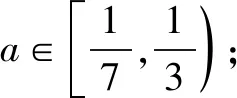
数学解题本质上就是一个不断转化的过程，将未知的问题转化为已知的问题.这种思想可以帮助我们解题，也可以帮助我们改编题目.沿着此思路，就函数的零点，笔者又进行了如下的变形设计：

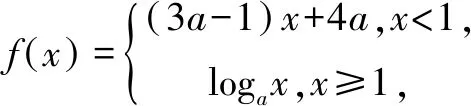
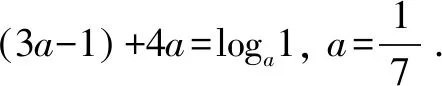
函数单调的情况研究清楚了，不单调的情况自然也就了然于心了.考虑此，笔者设计了如下的变式练习：

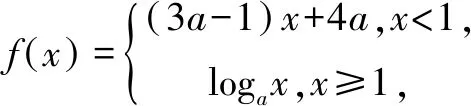
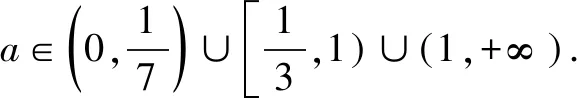
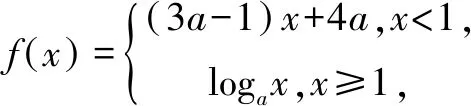
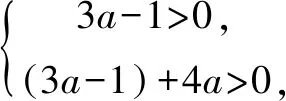
改编角度3 利用单调性求参数范围

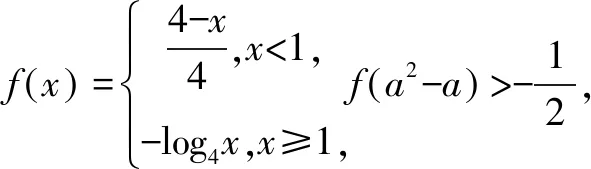
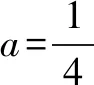
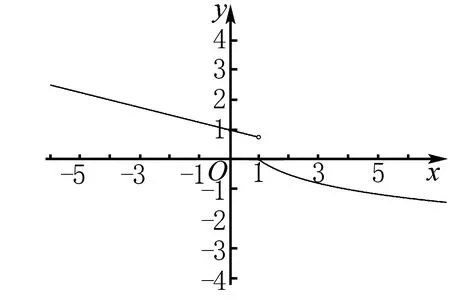
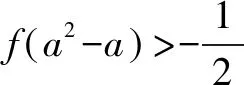
改编角度4 单调性与对称性

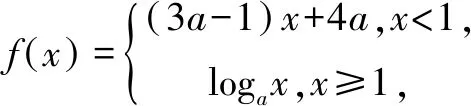
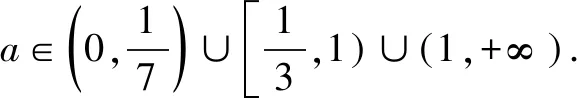
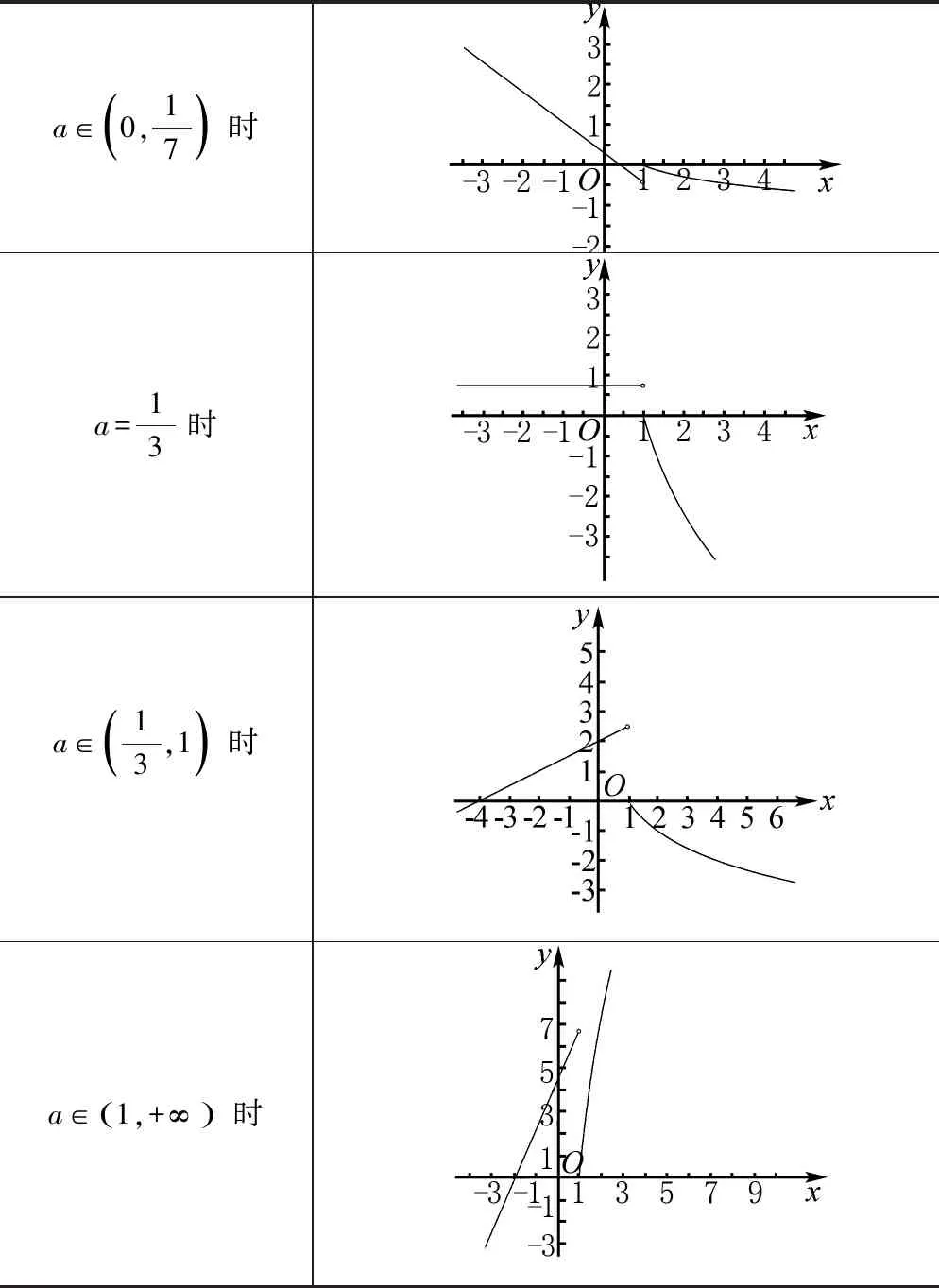
a∈0,17() 时a=13 时a∈13,1() 时a∈1,+∞() 时

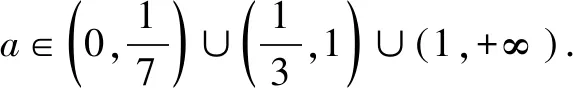
由本题可以进一步体会图象的重要性.若单纯地借助解析式进行代数推导将陷入复杂没有头绪的计算之中.

改编角度5 单调性与极值、最值

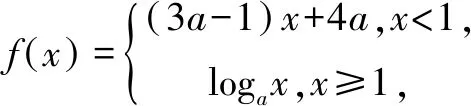
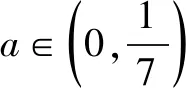
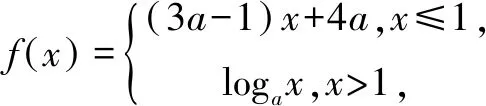
感悟1.解析式与与图象是函数的两种非常重要的表示方法，通过解析式研究性质可以锻炼学生的逻辑思维、数学抽象，要求学生对概念有深刻的认识，对函数有本质的理解，而通过图象获取函数的性质在解决小题时的优点更为显著.图象提供了更多的形象思维，更直观、易于理解，且性质一目了然.笔者在教学过程中针对此类题目总结了如下的口诀，深受学生喜欢.

遇见函数心莫慌，借助图象来帮忙.

慧眼识珠多发现，性质利用是关键.

含有参数困难增，留心观察变不变.

困难就像雾霾天，大风起兮蓝天见！

2.作为教师，要勤于思考，善于改编，用尽量少的题面帮助学生梳理尽量多的知识.教师的首要职责之一是不能给学生下列印象：数学题相互之间几乎没有什么联系，与其他事物也根本毫无联系.因此在同样的问题背景下改编设问，知识之间的联系更容易产生，知识网络更容易形成，更有利于学生的整体认知及思维形成.