解析数学高考压轴题的变化 确立高考复习对策

李 伟

(辽宁省鞍山市第三中学 114000)

纵观2019年全国高考数学理科试卷，其最大变化一是概率统计题、或解析几何题出在21题位置.二是导数应用题出在20题位置.由此自然产生一些联想，这种变化对高三复习将带来怎样的变化？下面来分析探讨这个问题.

一、关于压轴20题位置的导数问题分析与备考建议

全国一卷20题已知函数f(x)=sinx-ln(1+x)，f′(x)为f(x)的导函数，证明：

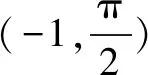
(2)f(x)有且仅有2个零点.

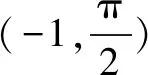
(2)证明f(x)有且仅有2个零点，从“形”的层面思考是函数y=f(x)的图象与x轴有且只有2个交点.转化为从“数”的层面思考是借助函数极值点、单调性的整合来实现上述“形”的意义，向“数”的意义转化.

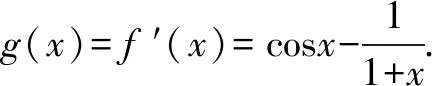
(2)函数f(x)定义域为(-1,+∞).f(0)=0，所以x=0是f(x)一个零点.

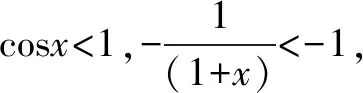
又f(0)=0，所以在(-1,0)内f(x)无零点.

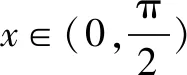
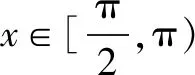
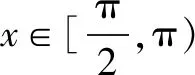
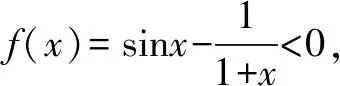
综上，f(x)有且仅有2个零点.

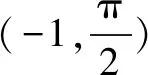
从问题(2)解题过程看，与以前导数压轴21题比较，变化的：一是减轻了构造函数的难度.二是减轻处理不等式放缩的技巧.不变的：一是数形结合、分类讨论等数学思想要求并没有减轻.二是反复从函数单调性概念及性质、导数等多角度考察函数单调性仍是高考重点.三是借助问题(1)来解决问题(2)的承接关系没有变.

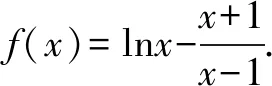
(1)讨论f(x)的单调性，并证明有且仅有两个零点;

(2)设x0是f(x)的一个零点，证明曲线y=lnx在点A(x0,lnx0)处的切线也是曲线y=ex的切线.

解题分析对于问题(1)讨论f(x)的单调性，通过解导函数构成的不等式、增(减)函数的概念和增(减)等单调函数的性质仍然是讨论函数单调性这类问题的基本思路.

对于证明有且仅有两个零点，从“形”的层面思考是函数图象与x轴(或者构造两个函数的图象)有两个交点(从函数图象看，结果是很显然的).从“数”的层面讲零点存在定理、函数单调性、极值点等知识点的整合都是处理这类问题的通性通法，只要注意因题而异、灵活使用即可.

对于问题(2)而言，解决问题的想法很直接，证明曲线y=lnx在点A(x0,lnx0)处的切线方程也是曲线y=ex在某点处的切线方程就可以了，余下的就是求切线方程问题了.

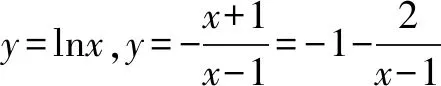
f(e)<0,f(e2)>0，所以函数f(x)在区间(1,+∞)上有唯一零点.

f(e-1)>0,f(e-2)<0，所以函数f(x)在区间(0,1)上有唯一零点.

综上，f(x)在定义域内有且仅有两个零点.

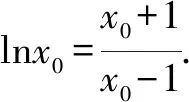
同理曲线y=ex在点(x1,ex1)处的切线方程为y=ex1x+ex1-x1ex1.

所以曲线y=lnx在点A(x0,lnx0)处的切线也是曲线y=ex的切线.

备考反思问题(1)的难度从解法看，难度与以前相比有所下降，但考查的内容没有变化，方法选择更加灵活，就上述给出的解题方法，简便易懂，不需要复杂求导运算.所以备考要注意一题多解和宽泛的通性通法的积累与运用，不拘泥与某种特定方法进行训练.

问题(2)的难度与以前的要求也降低了，但对切线概念的理解，切线公式的运用要求在加深.所以，尽管此处围绕切线方程涉及的知识点没有什么新意，但公切线是平时备考很少训练的，所以备考要注意挖掘概念、公式深层次的理解和宽泛的应用.

全国三卷20题已知函数f(x)=2x3-ax2+b.

(1)讨论f(x)的单调性;

(2)是否存在a,b，使得f(x)在区间[0,1]的最小值-1为且最大值为1？若存在求出a,b的所有值；若不存在，说明理由.

解题分析(1)用求导，再解导函数解不等式，即可解决讨论f(x)的单调性.

(2)从直观看，已知最大、小值，所以可以利用求最值的方法列出两个方程式，从解方程组角度思考，a,b的值是可求出的.

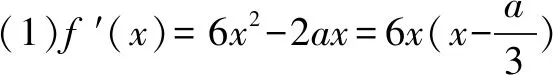
当a=0时，f′(x)≥0，所以f(x)在(-∞,+∞)为增函数.

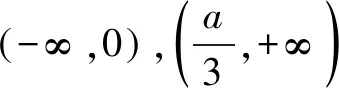
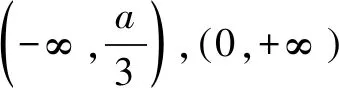
(2)当a≤0时，由(1)知f(x)在[0,1]上为增函数，所以此时a=0,b=-1.

当a≥3时，由(1)知f(x)上为[0,1]上为减函数，所以此时a=4,b=1.

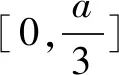
综上，a=0,b=-1，或a=4,b=1.

备考反思

问题(1)的求解过程是求导，解导函数不等式，讨论a与0的大小.这些都是导数部分复习备考的通性通法，没有难度，解题思维含量比较低.

问题(2)通过求函数最值列不等式组，求解a,b的值.这些也都是通性通法，没有难度.就本题涉及的分类讨论、数形结合的思想也是平时备考中重点训练的.

二、关于压轴21题位置的概率统计问题分析与备考建议

全国一卷21题为了治疗某种疾病，研制了甲、乙两种新药，希望知道那种新药更有效，为此进行动物试验.试验方案如下：每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠，随机选一只施以甲药，另一只施以乙药，一轮的治疗结果得出后，再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时，就停止试验，并认为治愈只数多的药更有效.为方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分，乙药得-1分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分，甲药得-1分；若都治愈或都未治愈则两种药均得0分，甲、乙两种药的治愈率分别记为α和β，一轮试验中甲药的得分记为X.

(1)求X的分布列；

(2)若甲药、乙药在试验开始时都赋予4分，pi(i=0,1,2,…,8)表示“甲药的累计得分为i时，最终认为甲药比乙药更有效”的概率，则p0=0，p8=1，pi=api-1+bpi+cpi+1(i=1,2,…,7)，其中a=P(X=-1)，b=P(X=0)，c=P(X=1).假设α=0.5，β=0.8.

①证明：{pi+1-pi}(i=0,1,2,…,7)为等比数列；

②求p4，并根据p4的值解释这种试验方案的合理性.

解题分析问题(1)求X的分布列，先确定X的取值，再计算出每个X的取值对应概率，列出分布列表即完成.此为求解分布列问题的常规解题步骤.

问题(2)①是证明：{pi+1-pi}(i=0,1,2,…,7)为等比数列；从通性通法角度讲，就是用等比数列的定义，解题关键是由已知条件出发推出pi+1-pi=q(pi-pi-1)的形式即可.

问题(2)②一是求p4，二是根据p4的值解释这种试验方案的合理性.

注意到(2)①与(2)②的承接关系，自然想到运用数列累加法和等比数列求和公式即可求出p4.

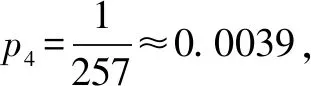
略解(1)由题意，X取值分别为-1、0、1，则P(X=-1)=(1-α)β，P(X=0)=αβ+(1-α)(1-β)，P(X=1)=α(1-β).分布列表略.

(2)①由问题(1)得：a=(1-α)β=0.4，b=αβ+(1-α)(1-β)=0.5，c=α(1-β)=0.1. 所以，pi=0.4pi-1+0.5pi+0.1pi+1，整理得：pi+1-pi=4(pi-pi-1)，因此，{pi+1-pi}(i=0,1,2,…,7)为等比数列；

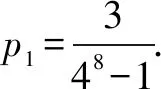
又p4=p4-p0=(p4-p3)+(p3-p2)+(p2-p1)+(p1-p0)=p1(43+42+4+1),

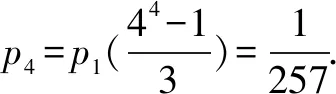
备考反思问题(1)是求分布列，其解法属于通性通法，不需要对概念的深刻理解.

对于问题(2)来说，难度比较大.难度之一是利用小概率事件对结论进行否定(肯定).学生对逻辑上的否定(肯定)是比较熟练的；用相关性、独立性检验等统计知识否定(肯定)也可以，因为教材上有一定量的介绍；用小概率事件来否定(肯定)某个结论(做法)学生就不太容易把握.主要原因是独立性检验虽然是建立在小概率事件上的两个事件独立与否的判断，但在教学中其理论部分要求较低，重点突出运用，导致其理论基础不牢.所以建议复习备考还是要深挖知识形成过程，重结论运用、轻基础理论建构、轻知识形成过程等做法是不可取的.难度之二是概率与数列的综合，尽管所用数列知识和解题方法，也是通性通法，没有特殊、高超的技巧要求，但平时缺乏这些知识点交汇使用的训练，导致运用生疏.所以，备考中在坚持夯实单元知识基础的同时，变换不同知识点之间的交汇训练还是应该坚持的(如：函数、导数、数列、概率、统计等主干知识之间的交汇).难度之三是概率统计类题目阅读量大，对语文学科阅读能力要求很高，所以，数学科培养学生阅读能力，通过阅读训练提升学生提取数学信息、选择解决问题的数学工具显得十分重要，对此在复习备考中要保持一定的耐心.

三、关于处于21题位置的解析几何问题分析与备考建议

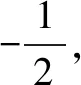
(1)求C的方程，并说明C是什么曲线;

(2)过坐标原点的直线交C于P,Q两点，点P在第一象限，PE⊥x轴，垂足为E，连接QE并延长交C于点G.

①证明：△PQG是直角三角形；

②求△PQG面积的最大值.

解题分析问题(1)比较显然.

对于问题(2)①证明△PQG是直角三角形，解析几何中的通性通法是斜率之积为-1，本题虽然运用“设而不求”、“韦达定理”，但，其中最大亮点是为简化运算采取的化简代换，此举不仅简化运算，还极大提高解题效率.

对于问题(2)②求△PQG面积，采取基本公式求解即可，没有技巧.求其最大值处亮点同样是为简化运算采取的化简代换，至于用导数、还是均值不等式求最值都是通性通法要求.

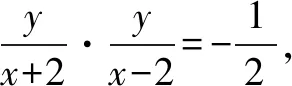
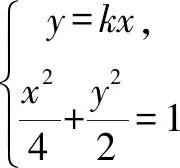
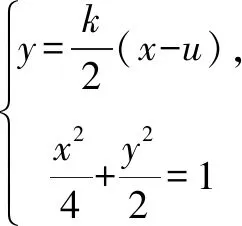
所以PQ⊥PG，因此△PQG是直角三角形.

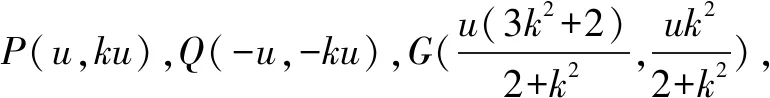
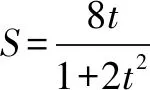
备考反思为达到化简运算的目的进行代换法是解决复杂运算的一个有效的做法，建议在复习备考中应该给予重视.通性通法中的“设而不求”、“韦达定理”、“讨论直线斜率存在性”等仍然是复习备考重点.另外，高考不给图形，显然是要求学生根据题意自己画图.所以，规范的、体现数量关系的画图要求在备考中是要强调的.

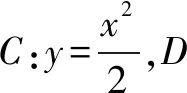
(1)证明：直线AB过定点;

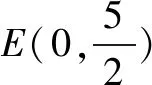
解题分析(1)直线过定点的基本想法是：点斜式y-y0=k(x-x0)方程中斜率为变量时，该直线过定点(x0,y0).也可以从y=kx+b入手，寻求k,b的关系，转化为点斜式研究定点.

(2)借助圆的切线性质，求出直线方程，将四边形ADBE的面积分解为两个三角形面积的和，借助点到直线距离求高，两点间距离求底边长，即可完成四边形面积求解.

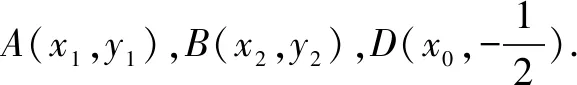
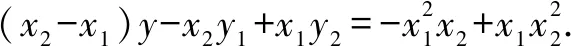
当x1≠x2时，化简得：x1x2=-1.

当直线AB斜率存在时，此时有x1≠x2.

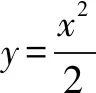
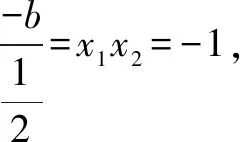
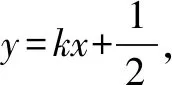
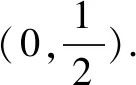
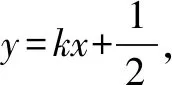
x2-2kx-1=0.

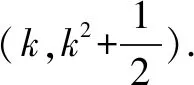
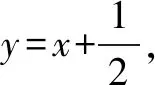
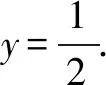
备考反思在解问题(1)时，“设而不求”、“韦达定理”仍是考查重点.如果讲新意就是借助求导来求斜率.综合上述，本题虽然作为压轴21题，考查通性通法仍然是重点.

对于问题(2)，考查的知识点比较多，但缺乏考查深度，所涉及的解题方法和技巧也是复习备考中的通性通法，没有新意.

所以解析几何的复习备考还是要强调通性通法，强调知识落实；解题时强调相关小题中的传承递进关系.

通过上述压轴题的剖析，概括而言，“新”体现在：一是知识点交汇比较新，如：概率与数列的整合.二是变换考查解题技巧，如：代换法.三是变换题目位置的设置，如：21题的导数转为20题等.“旧”体现在：一是仍然是考查通性通法.二是“新”只体现在知识点的并列，而不是融合；代换法也是“六大核心素养中的要求内容”.所以，在今后复习备考中，抓通性通法、抓知识基础、抓知识的可能交汇、抓学生的解题自信，以此培养学生分析、解决问题能力和意志品质，提升学生数学学科核心素养是复习备考的主题.