医学与社会科学领域中基于研究设计的常用统计方法选择指南

傅 强

圣路易斯大学公共卫生与社会公正学院流行病与卫生统计系，圣路易斯市，美国，63104

人类获得知识和解决问题的方法有很多种，有的凭自己以往的经验和直觉，有的向年长有经验的智者请教，有的回顾历史的案例，有的通过一种理性的系统的方法来寻求答案。科学就是一种方法论和系统论。科学研究产生的知识即科学知识并非基于个人观点、感受和直觉，而是建立在客观基础之上，通过谨慎的观察，使用系统的、有控制的、有条理的方法获得的故相较于其它方法，它的结论是更可靠和可信的。研究的目的是寻求问题的答案并获得新知识，科学研究依其功能可分为基础研究和应用研究。前者主要目的是发现新知识，是否实用不是其关注的焦点；后者主要目的是解决现实问题，其研究的场所不在实验室而在社会。医学与社会科学的很多研究都属于应用科学。科学研究依其观念的不同又可分为理论研究和实证研究。前者是推理性和抽象的研究；后者是归纳性的研究，即对许多现象的观察和各种经验的总结得出结论或支持理论。两种类型的研究在科学实践中相辅相成，共同帮助人类获得知识和解决问题。医学与社会科学研究多采用实证性研究，不管什么类型的科学研究，其决定性特征就是科学方法。13世纪的哲学家和科学家罗杰·培根指出科学方法是一切科学的基础。科学方法提供了一整套清晰和一致的收集、评估、报告信息的准则。学者们一般认为科学方法包含实证方法、观察、问题、假设、实验、分析、结论和复制等关键要素[1]。科学研究的方法大致可分为两类。一类是是定性研究法，它的主要目的是细致描述特定环境(如医院、学校、社区、商店、工矿企业等)中的现象，深入了解在特定环境中被研究的人(例如病人、医护工作者、学生、居民、消费者、职工等)的关切和感受，提供创建理论的基础和思路。其结论反映了被研究者对现实问题的看法和答案，故具有较大的主观性，多为探索性，不一定具有普遍性，不适用于大规模调查。另一类是定量研究法，它适用于大规模的调查。它要求对数据收集的方式有严格的设计，尽量客观地降低或排除人为的影响，数据收集要靠准确而可靠的测量工具，数据管理要科学，使用统计学方法分析数据，得出的结果具有广泛性、肯定性、前瞻性，或具有因果关系。一个学科的成熟与否可以从其量化的程度看出。研究设计发生在每一科学研究项目过程的早期，数据分析发生在科学研究过程的后期阶段，但两者紧密相关。什么样的研究设计决定了什么样的分析方法，根据不同类型的问题(如描述、预测、解释)研究设计可分为实验性研究设计和观察性研究设计。后者包括队列研究、病例对照研究、横截面研究(如图1所示)。随着近30年来统计学方法的迅猛发展，面对复杂繁多的统计方法，如何根据研究设计选择正确的统计方法，很多研究者感到缺乏足够的知识，需要清晰实用的方法指南；同时国内外的统计学专著往往将研究设计与统计分析方法分开论述[1]，这样的安排有其原因和优势，但同时也使读者难以看清两者互相交织的关系。因此本文将结合每一种研究设计类型讨论统计分析方法的应用原则。

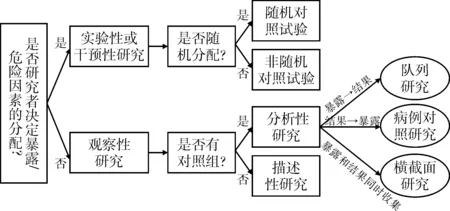
图1 研究设计分类图

1 实验性研究设计中统计方法的使用

实验性研究设计用于研究一个因素对另一个或几个事件之间的因果影响。此研究要求对研究的环境可以操控，目的是将被研究的因素与其他任何外界干扰结论的因素剥离出来从而通过人为改变被研究的因素，观察预期的结果或现象是否会产生。最常见的是随机双盲对照设计，这种设计代表了最严格的研究设计，被誉为研究设计的金标准，多用于实验室研究。在数据分析领域，各种因素或现象被转化后称作自变量或者因变量。因变量可以表达为一系列自变量的函数。实验性研究设计的特征是有一个可以控制操纵的自变量(即因素)，排除了其它外界干扰因素，实验结果即因变量的观察具有重复性，通过改变自变量可以观察到因变量在其影响下的相应变化。例如在评估新药疗效时将患某疾病的病人随机分配到治疗组和安慰剂组，治疗组别即自变量。在足够的样本量下，两组病人在各方面都非常相似甚至相同而唯有用药不同。如果病人对治疗有不同的反应，则可以确定是新药的效果。如果病人的反应是可以量化的连续型因变量，例如血脂、血压等，且该因变量在两组病人中分布符合正态分布，则可用t检验进行假设检验即两组的均值是否相等。如果病人随机分配到两个以上的组别里，则方差分析(analysis of variance，ANOVA)可用于假设检验即多组的均值是否相等[2]。这两种统计方法均适用于分析一个分类型自变量与一个连续型因变量之间的关系。如果因变量在两组或三组以上的病人中分布是不对称的，则分别使用非参数检验中的Wilcoxon秩和检验和Kruskal-Wallis检验。如果因变量也是分类变量，则可使用皮尔逊(Pearson)或似然比(likelihood ratio)卡方检验。由于随机双盲对照的实验设计较好地去除了干扰因素，因此使用统计分析方法比较简单。

如果因变量是生存时间(即记录经历多久结局事件发生)，例如肥胖者接受干预后体重降到正常的时间，某疾病住院日长短等问题则需要用生存分析的统计方法[3]。例如使用log-rank检验或Wilcoxon检验比较治疗组与对照组的癌症生存概率的差别。

在现实社会中由于许多客观条件和因素的限制，实验设计在社会科学领域几乎难以做到双盲，但应尽量做到随机对照。例如评估一种戒烟的新型行为干预方法，吸烟者可以随机地分配到干预组和对照组，使两组研究对象的各种特征均相似。对照组使用当前标准行为干预法，干预组则使用针对吸烟者自身特征而量身订制的戒烟干预方法。此时难以做到双盲。另外，有时随机原则在实际中也难以实现，例如一项研究计划通过实验性研究设计证明参加医疗保险可以提高妇女宫颈癌的早期诊断率。在实际操作中随机分配一部分妇女参加医疗保险，另一部分妇女不参加医疗保险，然后去追踪观察有医疗保险的妇女宫颈癌的早期诊断率是否高于没有参加医疗保险的妇女，研究设计上不可行也有违伦理。故在社会科学领域里可以应用实验性研究设计的场景较有限，例如某些行为干预和医疗服务市场研究时可以考虑该研究设计。

2 队列/纵向研究设计中统计方法的使用

它是选定一组研究对象对之跟踪观察一段时间记录下期待事件/结果的发生，它对与事件密切相关的敏感/暴露因素没有控制。此类资料收集费时费力，周期较长，成本较高。因为原因在前、结果在后，故此研究设计较其他观察性研究设计更有可能显示出自变量与因变量之间潜在的因果关系，但其结论仍然无法断定因果关系。它与实验研究设计的根本区别在于前者没有双盲随机的机制。例如假定暴露因素是是否接受了某种干预，研究对象通过自我选择是否接受该干预，由于没有随机分配的机制，因此干预组和对照组在很多方面都不相似，故在确定干预对预期结果的效果时需要将其它混杂因素对预期结果的影响加以排除。前述t检验、方差分析、卡方检验、非参数检验等方法尽管可以使用，但因为这些方法缺乏控制混杂因素影响的能力而无法给出肯定的结论，一般较少使用。

对这类观察性资料常用能控制混杂因素影响的统计方法是回归方法，最常用的回归方法是广义线性模型(generalized linear models)[4]。例如将重要的混杂因素转化为协变量代入到广义线性模型中加以控制。广义线性模型包括一组指数方程模型例如一般线性模型、logistic回归、对数线性模型、泊松回归、伽玛回归，因此它适用于不同类型的因变量。如果预期结果是连续型因变量且符合正态分布则选用一般线性模型(general linear model)，若连续型因变量不符合正态分布则选用分位数回归模型(quantile regression)[5]；如果预期结果是二分类、有序多分类、或名义多分类变量则选用logistic回归；如果预期结果是计数型因变量则选择泊松回归或负二项回归。广义线性模型对自变量的类型和分布没有限制。

由于纵向研究设计允许在不同时间观察不同事件的发生，此类资料适合于中介效应分析(mediation analysis)和路径分析(path analysis)方法[6]。图2为一个简单中介效应示意图。X代表自变量，M1和M2代表两个中介变量，Y代表因变量，箭头代表对应的回归系数，即每一对变量间相关的程度。在时间序列上X先发生，接着M1和M2发生，最后Y发生。M1和M2既是X的因变量，也是Y的自变量。此图还提示X直接影响Y，还通过M1和M2间接影响Y。如果分析显示所有箭头代表的回归系数都显著性地不等于零，则提示M1和M2有显著性中介效应。其结果有助于理解X影响Y的机制，也可对如何控制和改变X对Y的影响提出建议。

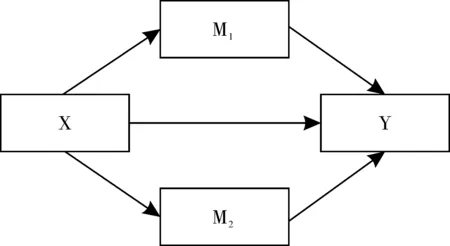
图2 中介效应模型示意图

在医学与社会科学领域中，很多数据通过调查问卷的方式获取，除少数观测变量具有较高的信度外，观测变量常常出现准确性较差，测量误差较大，信度较低的问题，其后果是中介模型估计出X，M1，M2，Y之间的关系出现偏差，从而无法检验出X影响到Y的真实机制。在这种情况下，可以用潜变量代替显变量(即X，M1，M2，Y)并使用结构方程模型(structural equation modeling)来分析[7]。图3为结构方程模型示意图。椭圆形代表潜变量，长方形代表外显变量，箭头代表回归系数。潜变量是不可以直接观察到的变量，但它可以通过相应的可观测的外显变量推导出来。现实生活中有许多现象是不能直接观测到但可以通过其外在表现而间接观测的。例如一个人的爱好可能是无法直接观测的，但如果人们看到他经常去打球、跑步、健身、看体育比赛、追踪体育新闻等，人们依此可推断出他有体育爱好。另外很多疾病是无法直接观测到的，但可通过症状、体征、病理变化等诊断出疾病。潜变量与显变量之间的一项重要差别就是前者没有测量误差。故中介效应的估计更准确。

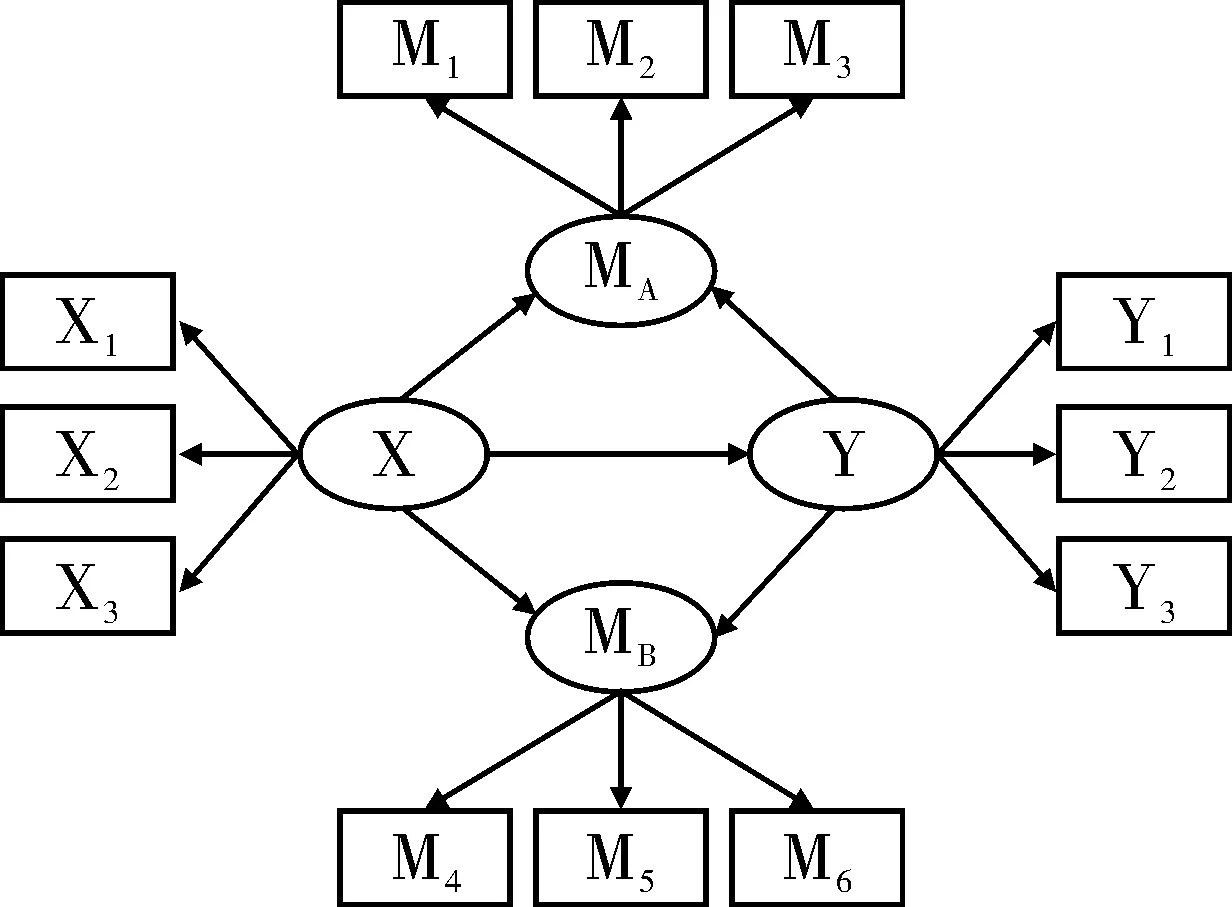
图3 结构方程模型示意图

如果研究目的不仅仅是反映观察期间内事件发生的概率，而是更关注何时事件会发生的概率或风险率则需要用到生存分析。例如癌症手术后五年内不同时间生存的概率和死亡的危险率及其影响因素，某疾病不同住院时间的概率及其影响因素等。Kaplan-Meier(K-M)生存概率估计法可用于估计在某一时间后的生存概率。Cox比例风险回归和Weibull回归最常用于此类问题分析。如果在观察期间同一事件多次发生且每次事件发生的具体时间可能不同，例如心脏病病人反复住院、戒烟多次失败、肿瘤多次复发等现象，如需对何时同一事件会反复出现的危险率及其影响因素进行研究，则使用分层Cox比例风险回归模型加上稳健方差估计(robust variance estimation)方法分析资料[8-9]。

近年来随着数据收集方法的提高，纵向研究设计在医学与社会科学领域使用得越来越多。例如针对研究对象在跟踪观察期间内定期反复进行测量，这样得到的数据往往不再相互独立，即同一个体的多次观测数据之间存在某种相关性，因此传统的广义线性模型不再适用。统计学家们对传统的广义线性模型加以改造扩展以适用于此类数据，发明了混合线性模型和广义估计方程(generalized estimating equation)[3,10]。前者又称多水平线性模型或成长曲线模型。该模型可以根据所有个体随时间变化的结局而估计结局变化的平均趋势以及影响趋势的因素。此方法已成为分析纵向设计资料的标准方法。广义估计方程与广义线性模型结合亦常用于纵向设计资料的分析，它用于估计因变量和自变量在群体中的平均相关性而不在于估计事件变化的平均趋势。

3 横截面研究设计中统计方法的使用

它同时收集结果以及影响结果的因素即自变量与因变量之间无时间上先后发生顺序， 多用于量化群体的不同特征之间的关系。该研究设计的优点是资料收集的成本较低，时间较短。前述t检验、方差分析、卡方检验、非参数检验等方法均可以使用[2]。但因为这些方法缺乏控制混杂因素影响的能力而无法给出肯定的结论，一般较少使用。最常用的回归方法是广义线性回归模型。广义线性回归模型可以用于控制混杂因素的影响后研究目标群体中哪些特征变量是互相关联的[2]。例如某研究想分析社会支持程度与生活质量之间的关系。由于社会支持程度与生活质量均是通过相应的量表打分测量得到的变量，故自变量和因变量均为连续型变量，如果因变量符合正态分布，则可以使用一般线性模型。又例如某研究想了解哪些因素影响居民与家庭医生的签约，由于因变量是是否签约了家庭医生，故logistic回归适用于此类资料分析。

如果观测的变量出现准确性较差，测量误差较大，信度较低的问题亦可以使用结构模型方程的方法来降低测量误差，更准确地估计目标群体中哪些特点是互相关联的。例如在研究肥胖程度对心血管和肿瘤疾病影响时，需要对肥胖程度进行明确的定义，但其定义常常引起争议。有的从体重的角度来衡量肥胖，即使用体重指数(body mass index，BMI)；有的从脂肪分布的角度来衡量肥胖，即使用腰围、臀围、腰臀比。每一项指标都部分地代表了肥胖特征，但都不全面，导致使用不同的肥胖变量后，得出了不一致的肥胖对心血管和肿瘤疾病影响的结论。如果将肥胖处理成一个潜变量，通过体重、体重指数、腰围、臀围、腰臀比这些外显变量来衡量肥胖，则有助于更全面更准确地反映肥胖对心血管和肿瘤疾病的影响。结构方程模型就是适用于分析这类资料的统计方法[7]。又如心血管疾病是指一类疾病，具体包括多种具体的心血管疾病，例如急性心血管阻塞、中风、心力衰竭、心律失常，它们反映了心血管系统动脉粥样硬化的结果。由于心血管系统动脉粥样硬化的程度不易直接观测到，动脉粥样硬化也可以被视为是一个潜变量，具体的心脏病可以被视为动脉粥样硬化程度的指标。这个评估系统的建立可以使得临床医生和病人不用费时费力费钱的方法就能知道当某种心脏病出现时，动脉粥样硬化就到了何种程度，即用具体心血管疾病给动脉粥样硬化评级。这种研究适合于使用横截面设计和项目反应理论(item response theory, IRT)方法分析资料[11]。

在医疗卫生领域，人们常遇到分层结构(又称多水平)的资料。例如病人属于不同科室，科室属于不同的医院，医院分布在不同的区域。又如居民居住在不同社区或街道，不同社区或街道属于不同的城市。研究对象被不同水平的组合分成不同的群。群内研究对象的观测资料之间往往互相关联，但群间研究对象的观测资料互相独立。每一层各有其特征，且均对最底层的研究对象有间接影响。如果将多水平资料当作做同一水平的资料使用广义线性模型，依据高层次的特征与属性推测低层次中个体的特征与属性就会得出谬误[12]，这种错误称为生态学谬误(ecological fallacy)。正确的统计分析方法是使用多水平线性模型和广义估计方程[4,10]。

以上统计方法均是以变量为中心的方法(variable-centered methods)，旨在揭示变量之间的关系。在医学与社会科学研究中，往往存在较大的个体差异或异质性(heterogeneity)，针对不同类型的对象使用有针对性的对策才能产生最好的效果，在健康研究领域尤其如此。物以类聚，人以群分，人与人之间的千差万别既有生物方面的原因也有社会方面的原因。所以近年来在医学与社会科学研究中越来越多地开始应用以人为中心的统计方法(person-centered methods)，旨在揭示人群中存在的异质性和类别(尤其是潜在类别)。此时需要回答的是有多少类别及各类别特征的问题。有些情况下分类很容易很简单，例如按性别、年龄、民族、地域、职业分类等；有些情况则不容易进行分类，例如人格、价值观、态度、身体健康、心理健康等。它们没有单一直观的指标而是通过多个特征来显示。有意义的分类要达到两个目的：一是有几类以及每一类占多大的比例；二是每一类的特征是什么，受哪些因素影响。潜类别分析(latent class analysis)方法适用于分析用横截面设计收集而来的资料[13]。该方法将潜类别视为潜变量，该潜变量通过可见的具体特征即外显变量表现出来。例如某研究想了解在某特定人群中抑郁的程度有多少类，每类占多大比例，特征如何，不同类别受哪些因素影响。该研究可以根据国际疾病分类第十一版(International Statistical Classification of Diseases and Related Problems-11)提出的抑郁的九大特征[14]，用潜类别分析的方法找出最佳类别、相应的特征以及影响各类的因素。其结果可能有利于预防、治疗、资源配置等需要。

4 病例对照研究设计中统计方法的使用

该设计主要针对小概率的事件或结果。它将现在已有事件发生的研究对象，例如患某种疾病的病人作为一组，另外再配备一组无此结果的研究对象作为对照组，然后追溯两组研究对象之前是否暴露于相关的危险因素。该设计决定了结果就是因变量即病例或对照。如果自变量是分类变量则可用皮尔逊(Pearson)或似然比(likelihood ratio)卡方检验来分析自变量与因变量之间是否相关。为了控制混杂因素的影响，常用logistic回归研究目标群体中危险因素与结果是否相关。

如果病例与对照两组样本是配对样本且自变量是二分类变量，例如检验糖尿病与心肌梗塞之间的关系，每一位心肌梗塞的病人匹配一位同年龄和性别相同但没有心肌梗塞的病人，然后比较两组病人中糖尿病患病的差异，则需用McNemar检验[2]。为了控制混杂因素的影响，常用条件logistic回归(conditional logistic regression)研究目标群体中危险因素与结果是否相关，例如糖尿病是否增加心肌梗塞的风险[4]。

在配对设计中常用自身做对比，例如同一病人治疗前和治疗后疾病的变化，医疗服务改进前后同一病人满意度的变化等。这些资料分别适合用于McNemar检验和配对t检验[2]。如果需要控制外在因素的影响，则需使用条件logistic回归、多水平模型、广义估计方程[4,10]。

5 结论

统计方法繁多，每种统计方法都有适用的条件和范围，针对不同的研究采用最合适的统计方法对于每项研究的结果都是至关重要。选择最合适的统计方法可以从多角度来考虑，难以有唯一的答案。作者认为研究设计决定了统计方法的使用，没有在研究设计指导下的分析是没有实际意义的分析，本文旨在为在医学与社会科学领域一线工作的广大科研工作者提供如何根据研究设计的类型合理选择统计方法的实用指南。有一些统计方法适用于多种设计类型，另一些则适用面较窄(见表1)，对于统计结果的解释需要结合研究设计才能准确。

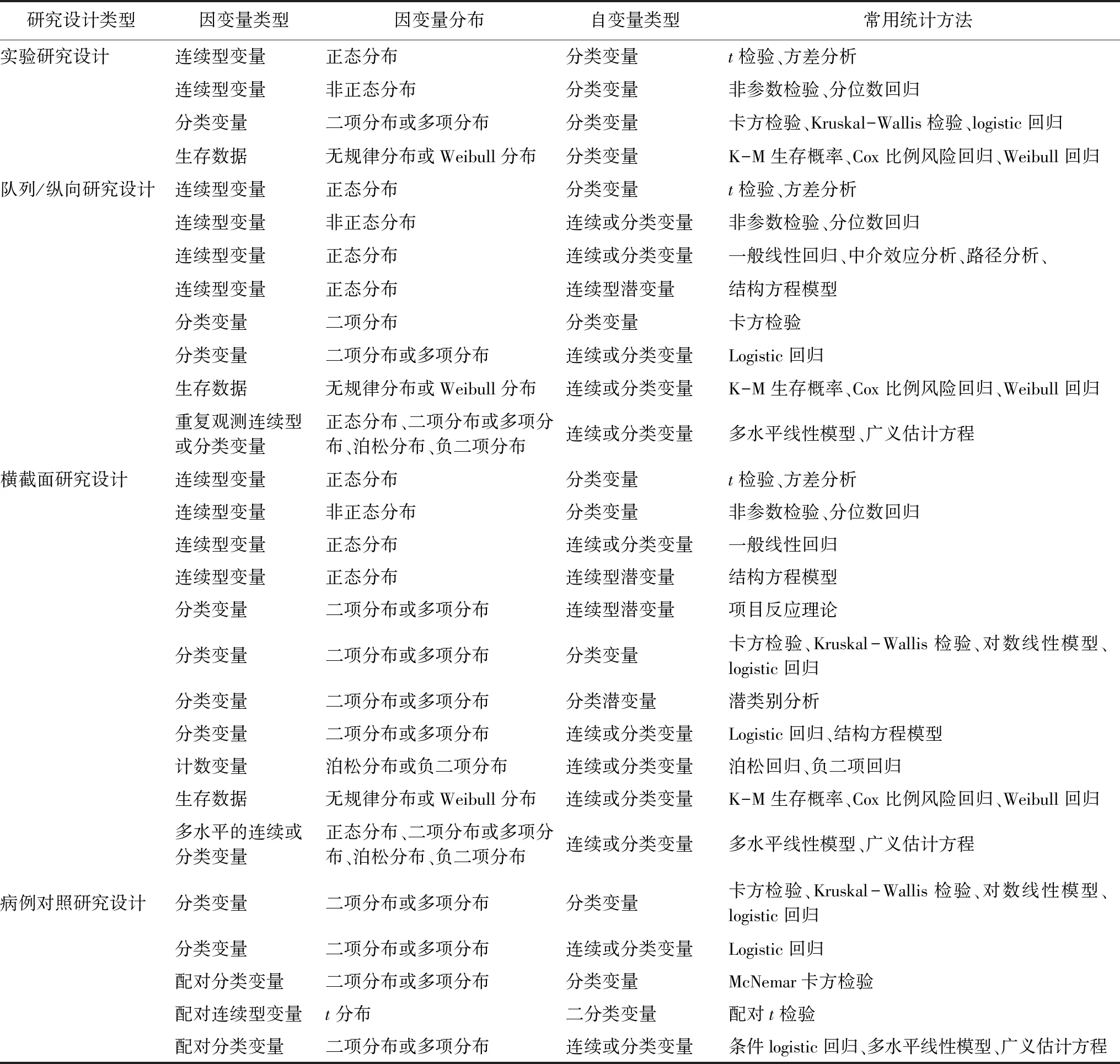
表1 研究设计类型、变量类型与常用统计方法之间的关系

由于统计方法选择的正确与否直接关系到分析结果的正确与否，广大科研工作者一方面可以通过加强自身统计学知识的学习提高正确使用统计学方法的能力；另一方面应多与统计学家组成协作团队，在研究项目刚开始或尚在计划阶段积极邀请统计学家参与计划，统计学家会根据后期资料分析整理与解释的要求在资料尚未收集之前对研究项目提出建设性的意见，极大地提高研究项目的成功率。