一类一阶差分方程周期边值问题正解连通分支的振荡及无穷多个正解的存在性
苏肖肖
(西北师范大学数学与统计学院, 兰州 730070)
1 引 言
近年来,对一阶常微分方程周期边值问题的研究已有诸多结果[1-6],而对一阶差分方程周期边值问题的研究则相对较少.比如,Sun[6]运用锥拉伸与压缩不动点定理获得了一阶差分方程周期边值问题
-Δx(t)=f(t,x(t+1)),t∈{0,1,…,T},
x(0)=x(T+1)
正解的存在性,其中T>2是整数,f:{0,1,…,T}×[0,∞)→R连续.值得注意的是,该文虽然获得了正解的存在性,但没有得到正解集的全局结构.
随着分歧理论的发展,一阶差分方程周期边值问题正解连通分支的走向问题也获得了一些结果,如Ma等[7]获得了该类问题从特征值处产生的连通分支是向左或向右分歧的,并给出了连通分支具有简单结构的条件.但据我们所知,对于一阶差分方程周期边值问题正解连通分支无穷多次振荡的结构性态尚未被研究.
本文的目的是研究一类一阶差分方程周期边值问题
-Δx(t)+q(t)x(t)=λa(t)x(t)+f(t,x(t))x(t),
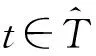
(1)
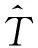
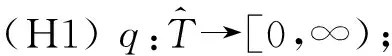

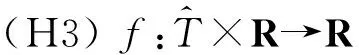
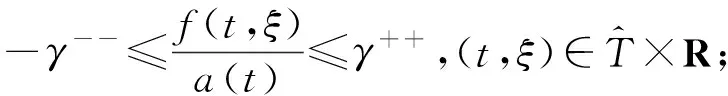
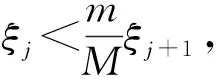
其中M,m分别是问题(1)对应齐次方程的格林函数的最大最小值.
记


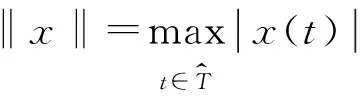
本文的主要结果如下:
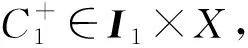
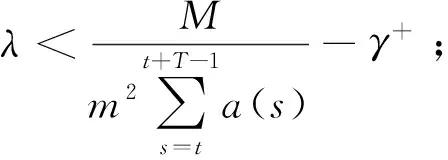
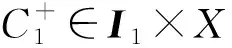
2 预备知识
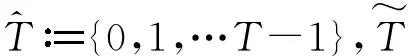
引理2.1(Krein-Rutman定理)[8]设E是Banach空间,K⊂E是一个锥且满足K°≠∅.设F∈L(E)是一个紧的强正算子.则r(F)>0,r(F)是F的一个具有正特征函数v∈K°的简单特征值,并且F再没有其他正特征值.
引理2.2(Rabinowitz全局分歧定理)[9]设E是Banach空间.考虑方程
x=μLx+N(μ,x),μ∈R,x∈E
(2)
假定
(A1) 算子L:E→E为线性紧算子;
(A2)μ0为L在E中的本征值,且其代数重数χ(μ0)为奇数,其中
(A3)N:R×E→E全连续,且
记C(μ0)为方程(2)的非平凡解集的闭包中包含点(μ0,0)的连通分支,则下面两种情形之一出现:
(i)C(μ0)无界;

引理2.3假设(H1)~(H3)成立.设h∈Y.则问题
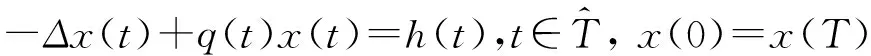
(3)
存在唯一解x(t),

(4)
其中
(5)

故
简单化简可得
即
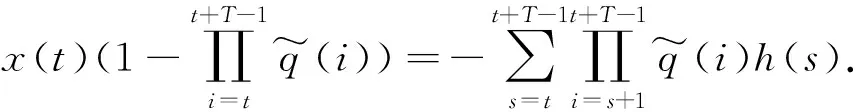
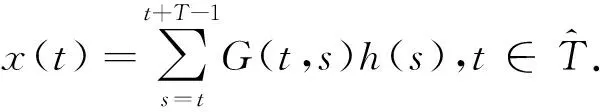
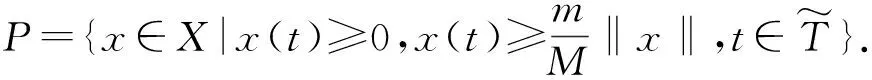

引理2.4假设(H1)~(H3)成立.则Aλ(P)⊂P且Aλ:P→P是全连续的.
证明 由P的定义,若x∈P,则
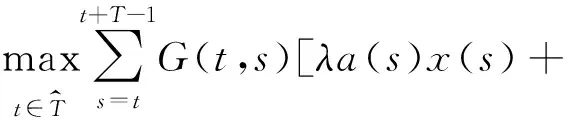
f(s,x(s))x(s)]≤
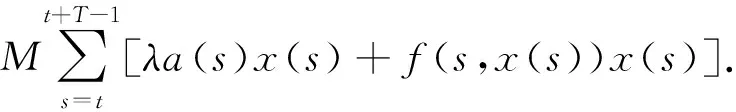
f(s,x(s))x(s)]≥
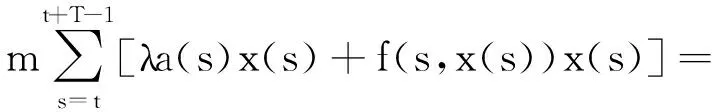
故Aλ(P)∈P.此外,由X是有限维空间易证Aλ:P→P是一个全连续算子.
令λ1是线性特征值问题
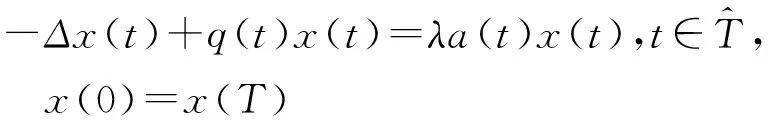
(6)
的一个主特征值,φ1是λ1对应的非负特征函数.
引理2.5假设(H1)~(H2)成立.则线性特征值问题(6)存在一个简单主特征值λ1>0,其对应的特征函数φ1∈X同样为正.
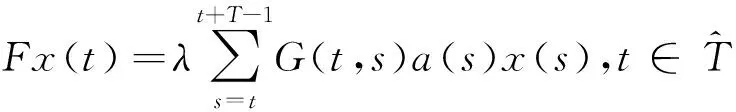
是一个强正算子,即Fx∈intP0,x∈P0{0}.由引理2.1,谱半径r(F)>0且存在φ1∈X,φ1>0使得Fφ1=r(F)φ1.因而λ1=(r(F))-1是线性特征值问题(6)的具有正特征函数的正特征值.
3 主要结果的证明

Lx-λa(t)x=f(t,x)x
(7)
方程(7)等价于
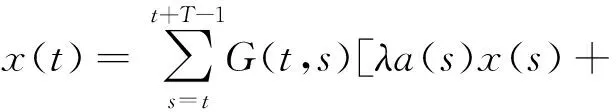

L-1[f(·,x(·))x(·)])(t).
记


其全连续的证明同引理2.4.则
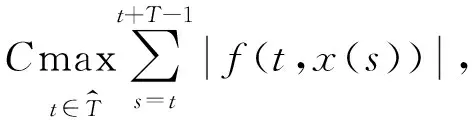
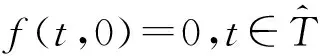
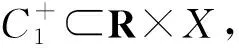
定理1.1的证明 因为
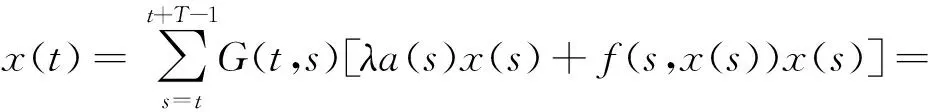
‖x(t)‖≥x(t)≥
所以
即
(8)
同理,
(9)
因为
等价于和分方程
而
所以
(10)
同理,
即
(11)
由(8)和(9)式可得
由(10)和(11)式可得
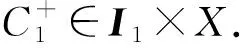
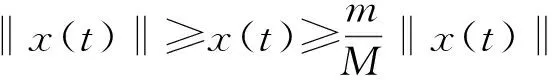

因为
γ+)a(s)‖x(s)‖,
所以
(12)
同理,若(λ,x)是问题(1)的任意正解,对某个整数j≥1,‖x‖=ξ2j有
(13)
结合(10)式和(11)式即得



