生物质固化成型机不同孔形受力分析*

何一波 严永林 黄 俊

（中南林业科技大学机电工程学院，长沙 410004）

生物质固化成型技术是在生物质能利用技术基础上发展起来的，是用于高值清洁利用农林剩余物、杂草藤条等廉价碳汇资源效果显著的技术之一[1-3]。影响生物质固化成型的因素有很多且十分复杂[4-5]，徐弘博[6]提出对模腔采用模孔与模芯组合的方式取代直接在模盘上加工模孔的方法，但是选择何种形状模孔却没有相应的理论支撑，仅仅依靠经验选择[7-9]。为此,本文在借助特征参数化建模软件的基础上设计了3种典型模孔结构，分析原料在3种不同孔形内挤压成型的受力情况，在探讨不同形状模孔优缺点的基础上提出复合型模孔结构，以期为生物质固化成型机的模孔选形和结构优化提供借鉴[10-15]。

1 不同孔形建模

图1 不同孔形模具Fig.1 Different hole molds

采用生物质固化成型机对原料进行挤压成型，选用不同形状的模孔，因孔形结构特征差异，在挤压成型过程中，原料在模腔内所受挤压力大小会不同[16-21]。因此借助特征参数化建模软件pro/e 5.0，设计圆形、方形和正三角形3种典型模孔结构，其结构参数为边长5 cm，长径比6：1（如图1所示），以探究不同形状模孔成型过程挤压特性。

2 模孔挤压特性理论分析

不同形状模孔在其压缩过程的挤压特性无法通过试验观察，因此，首先基于正方形模孔进行挤压特性的理论分析，然后以同样的分析方法得出圆形模孔和正三角形模孔挤压特性公式。正方形成型模孔如图2所示，其成型腔大端正方形边长为a，保型腔的正方形边长为b，成型腔段长度为L1，保型腔段长度为L2。

图2 正方形成型模孔示意图Fig.2 Schematic diagram of die square forming

先忽略图2正方形模孔进料端带锥角的成型腔部分（下文将对其受力情况进行分析），绘制保型腔段受力图，如图3所示，取其一微单元段dx作为受力分析对象。在模腔内生物质原料首先在压辊的作用下受到挤压力（dFx）的作用，然后在孔腔内产生摩擦力（dFf）以抵抗挤压力（dFx），由于模孔是固定的，生物质原料在孔腔内还会受到内壁对其产生的正压力（dPN）作用。

图3 生物质原料在正方形保型腔中的受力示意图Fig.3 The stress diagram of biomass particles in square holding hole

假设轴向挤压力dFx在正方形保型腔面积上是受力均匀分布的，则微单元段dx处受到的轴向挤压压强为：，受到的摩擦力dFf为：dFf=f·dPN·4bdx。由于原料被挤出模腔的最基本条件为：Fx≥Ff，即最低挤压成型要求：Fx=Ff，在dx微单元段上即：dFx=dFf，故b2dPx=f·dPN·4bdx。

由材料力学中广义胡克定律[10]可知:

式中：εx为原料在x轴向的应变；εy为原料在y轴向的应变；E为弹性模量，σx、σy、σz分别为物料在x、y、z轴向的应力，MPa；μ为泊松比。

原料在模腔挤压过程中σy=σz,将其带入（1）式中并化简可得：

上述只是考虑了不带锥角的保型腔段，现在对带有锥角的成型腔段进行受力分析。取其微单元段dx作为研究对象，如图4所示。从图中可以得出，原料能顺利被挤出的基本条件为：Fx≥Ff·cosθ，即最低挤压成型条件为：Fx=Ff·cosθ。体现在该微单元段上即：dFx=dFf·cosθ，微单元段受到的挤压力为：dFx=y2·dPx，受到的摩擦力：dFf=f·dPN·4y·cosθdx（式中b≤y≤a），将其带入得：y2dPx=f·dPN·4y·cosθdx，按照上面保型腔计算方法将其变换成微分形式：考虑积分上下限，然后列出积分表达式为：

式中:Lx为成型腔段微单元段距进料端的距离（0＜Lx≤L1），cm；θ为成型腔锥角，0 ＜θ≤30°；y为成型腔段微单元段的高度（b≤y≤a），cm。

上式（7）中存在y这一可变因素，为了便于推算出挤压力公式且变量不至于过多，可通过在成型腔示意图4的基础上延长成型腔斜边的线段，使其与中心线相交，得出相应的几何关系,从而将上式中的y进行替换。根据成型腔图4中几何关系可以得出：由这两个关系式的变化可以推出：y=将其带入式（7）中并对其两边进行积分，可以得出：

当Lx=L1时，也就是位于成型腔末端的压力，将带入上式可以得出:

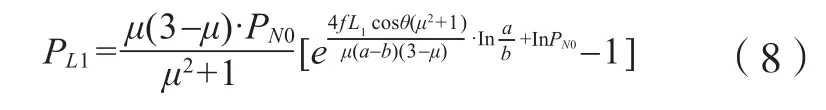
式中：PL1为成型腔内原料所受的挤压压强，MPa；L1为成型腔段的长度，cm；a为成型腔端面边长，cm。

为便于计算，在计算保型腔挤压特性时将积分起点理想化，起点设为了0，而实际起点是L1,故对上式（8）重新考虑积分下限，积分形式变为：

式中：L2为保型腔段的长度， cm。

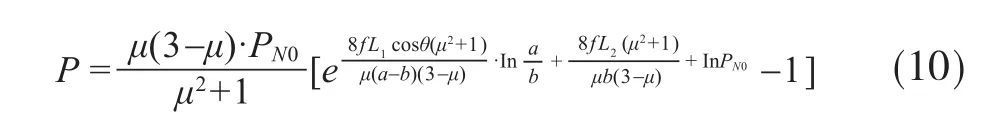
3 结果与分析

3.1 不同孔形挤压力公式比较分析

根据前面对正方形模孔挤压特性分析得出的挤压压强公式（10），可进一步计算得出正方形模孔的挤压力：

按照上一章节方法推导圆形模孔和正三角形模孔的挤压力：

从公式（11）、（12）和（13）可以看出，挤压力公式由轴向挤压压强P和面积A两部分组成。3个公式中，轴向挤压压强不同之处在于以e为底的指数函数上的幂指数不同，这里给定相同的长径比（正方形长径比指正方形孔腔的长度与其边长的比值，等边三角形长径比指等边三角形孔腔的长度与其边长的比值)、锥角、预压力和摩擦系数，根据指数函数的性质可以直观得出轴向挤压压强：P正方形＞P圆形＞P正三角形；再分析比较3种不同模型孔的面积A，分两种情况探讨:第一种情况假设3种模型孔的面积A都相同，可通过3种孔型的面积计算公式分别计算3种孔型的直径或边长，计算可得：b正三角形＞d圆形＞b正方形；第二种情况假设圆形孔直径和其他两种模孔边长相等(即假设d=b)，通过3种孔形的面积计算公式可得：A正方形＞A圆形＞A正三角形，因此，无论上述哪种情况都可以得出3种模孔挤压力：F正方形＞F圆形＞F正三角形，正方形模孔的挤压力最大。以上结果表明，不同形状模孔结构可显著影响挤压成型所需的挤压力。

3.2 不同孔形优缺点分析

从理论分析结果来看，3种形状模孔取任意模孔单独作为成型腔或保型腔，都各有优缺点。首先，取不同形状模孔作为成型腔，其进料端各有差异，在给定相同边长（直径）条件下，3种模孔面积：A正方形＞A圆形＞A正三角形，表明选取正方形模孔作为成型腔进料端进料量最大[22-27]，圆形模孔次之，正三角形模孔最小；其次，取不同形状模孔作为保型腔或成型腔，模孔制造的困难程度及成本也有差异，制作三角形模孔和正方形模孔均需设计制造特殊的非标准加工工具，投资成本高，而圆形模孔制作却有标准钻孔工具，不仅投资成本较低，而且容易实现；综上分析，考虑采用圆形模孔作为保型腔、正方形模孔作为成型腔进料端，即“外方内圆”的复合型模孔结构，较其他两种孔形具有进料口更大、进料量更多的优势，且圆形模孔作为保型腔制造[28-30]。

4 结论

通过上述理论分析和推导，得出以下结论：在生物质固化成型中，对圆形、方形和正三角形3种典型模孔的选择，可优先考虑方形和圆形模孔。在相同条件下，3种模孔中，正方形模孔的轴向挤压力最大，且在边长（或直径）相等的条件下，正方形面积也最大，可满足进料量最大的需求；从制造工艺考虑，采用圆形模孔结构，投资成本较低，而且制造上更容易实现。

综合考虑3种形状模孔挤压特性的优缺点，采用正方形模孔作为成型腔，圆形模孔作为保型腔，即“外方内圆”的复合型模孔结构更利于进料和挤压成型。