构建知识形成过程 提升学生数学素养——《20.4 课题学习 最短路径问题》教学设计

赖巧芳

(广东省广州市广州大学附属中学 510006)

一、教材分析

利用轴对称研究某些最短路径问题.

二、学情分析

作为初二的学生，面对具有实际背景的最短路径问题，会感到无从下手.对于直线同侧的两点，如何在直线上找到一点，使这一点到这两点的距离之和最小，一些学生会找不到解决问题的思路．

三、教学目标

1.知识与技能

(1)能利用轴对称的性质解决最短路径问题，体会图形变换在解决问题中的作用.

(2)在探索中，感悟﹑应用转化的数学思想．

2.过程与方法

通过让学生经历观察演示，动手操作，自主探究，合作交流等过程，培养学生解决问题的能力及数学建模能力.

3.情感与态度

利用多媒体，培养学生探究问题的兴趣.

四、重难点及其突破措施

1.重点：利用轴对称知识解决两点之间最短路径问题

2.难点：如何利用轴对称将最短路径问题转化为线段和最小问题

3.突破措施

(1)利用几何画板、数学视频显示将军饮马问题的本质，在学生脑海中加深印象.

(2)通过多媒体创设启发性情境，让学生积极学习.

五、教学流程设计意图

研究思路及活动设计意图认知维度复习与“最短”有关的工具记忆从简单问题入手,搭桥梁,构建转化路径理解归纳可以用轴对称将问题转化的条件特征,形成策略性知识理解基于策略性知识,形成画图步骤理解在新的问题情境中,判断是否可以用轴对称转化,并实施画图步骤应用,分析设计一个与最短路径有关的数学问题创造

六、教学过程设计

活动1 温故知新，知识储备

1.轴对称性质：对称点连线被对称轴垂直平分.

2.最值原理：两点之间，线段最短. 垂线段最短.

设计意图：复习轴对称性质，线段公理，为后续的学习做好知识上的储备.利用温故知新，运用最近发展区，激发学生的学习兴趣.

活动2 情境引入

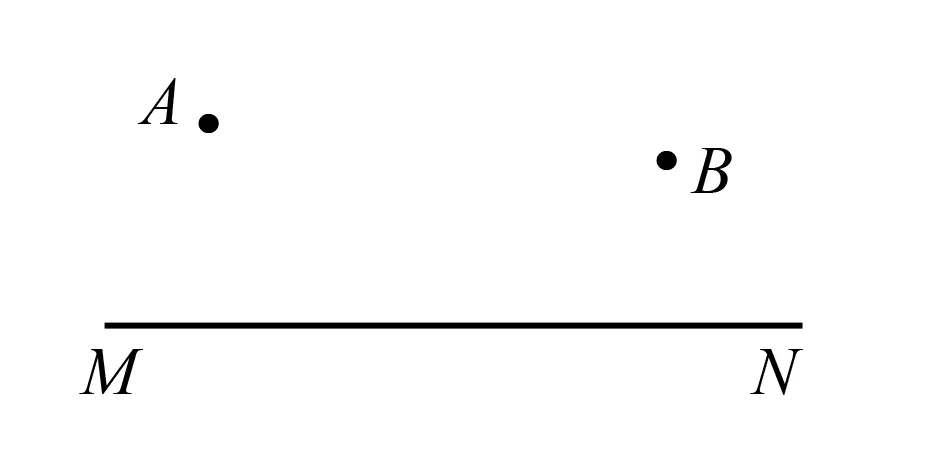
例1如图，有一位将军骑着马从A点的军营出发，先到河MN边让马喝足水，再返回河岸同侧的B点家中，该如何选择路线，让将军回家的路程最短？

画一画，并测量.展示、追问.

经过学生探讨，小组交流，最后师生共同归纳总结如下：

1.把同侧问题变为异侧问题，运用了转化思想.

2.利用轴对称的方法，化折线段为直线段，再结合“两点之间线段最短”的性质，就可以解决这类最值问题.

设计意图:及时小结体会轴对称的作用.

活动3 画龙点睛

画图步骤：1.明确直线和直线同侧的两点；

2.过其中一个点作关于这条直线的对称点；

3.连接对称点与另一个点，与直线交点即为所求.

设计意图:基于策略性知识，形成画图步骤.

活动4 智勇大冲关

1.如图，点A′与点A关于直线l对称，点B与点A在直线l的同侧，测得A′B=20 cm.若点P为直线l上的一个动点，连接PA、PB，则PA+PB的最小值为____.

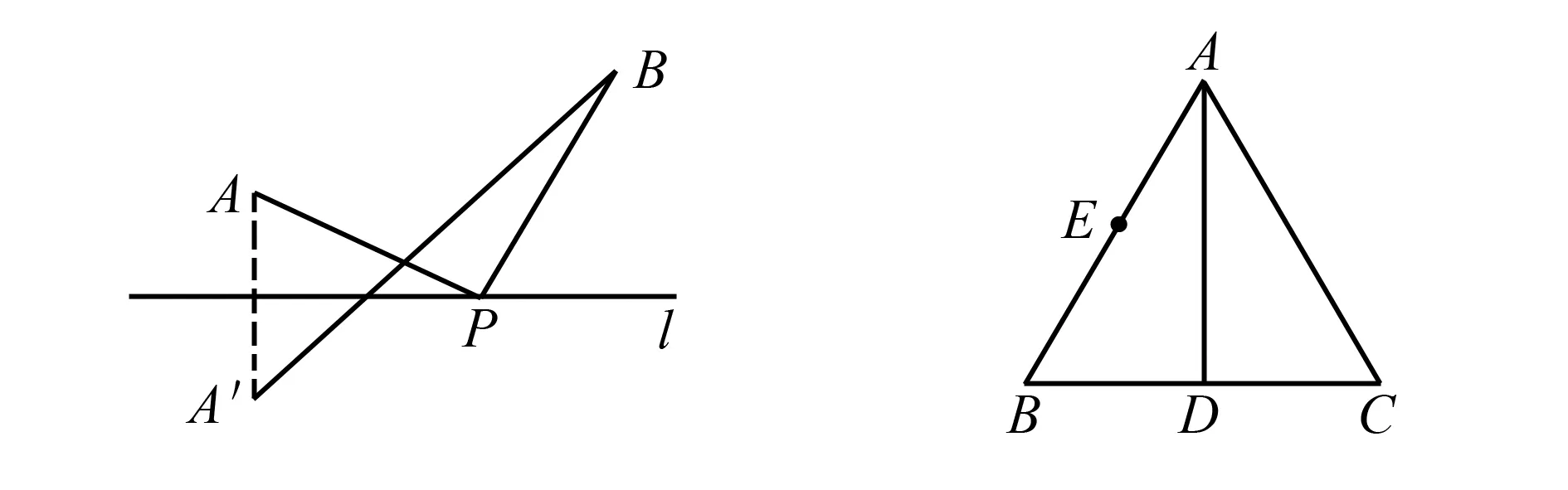
2.如图，在等边三角形ABC中，点E是AB的中点，AD是高，在AD上找一点P，使BP+PE的值最小.

设计意图:还必须结合不同的问题背景如特殊三角形、特殊四边形等.将运用这一基本事实解决具体问题常态化、系列化，确保学生对此类问题的真正理解和掌握.

活动5 更进一步

例2如图，一匹马从S点出发，先去OP上一处吃草，再去OQ河边喝水，然后再返回S点.该如何选取路线，使得经过的总路程最短？

学生思考交流，教师巡视.

设计意图:在交流中明白作法的合理性，让学生真正理解解决问题的方法.在小组合作学习中学生找到解决问题的方法，意在体现学生的合作意识.几何画板演示，让学生从数的角度感知作法的正确性.

活动6 举一反三(略)

活动7 课堂小结

转化关键：

最短路径问题—轴对称性质—两点之间线段最短

研究过程：

大胆尝试-寻求依据-小心证明-迁移延伸.

设计意图:从实际问题中建立数学模型.