例析与中点有关的辅助线的作法

宋明明

(北京市文汇中学 100022)

在初中数学的解题中，中点起着非常重要的作用.如果能用好、用活中点，不但能提高解题速度，而且能够提高解题的准确度，提高学生的发散思维能力，为学生的数学学习插上腾飞的翅膀.

线段的中点是几何图形中的一个非常特殊的点.在解决与中点有关的问题时，如果能适当地添加辅助线、巧妙地利用中点是处理中点问题的关键.但是由于含有中点的问题的辅助线作法灵活，不少学生难以掌握.

一、中位线

方法一(图2)

分析在△ABC中存在一个中点D，所以需要再找到一个中点才能构造出D为中位线，这时候我们自然想到要在AC上取中点，因为在BC上取中点会破坏AE=BC这个条件.

证明取AC的中点P，连接DP.

∵D、P分别为AB、AC的中点,

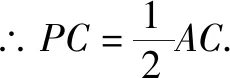
∵AE=BC,∴DP=PF,∴∠PDF=∠AFD,∴∠APD=2∠AFD,∴∠ACB=2∠AFD.

方法二(图3)

分析D为线段AB的中点，F为线段EC的中点， 自然联想到DF是某个三角形的中位线.这时需要构造一个△ABP，而且F必须是线段AP的中点，所以只需在AC的延长线上截取CP=AE.

证明在AC的延长线上截取CP=AE，连接BP.

∵F为EC的中点,∴CF=EF,∴CF+CP=EF+AE,即PF=AF,∴F为线段AP的中点.∵D为线段AB的中点,∴DF∥BP,∴∠AFD=∠P.∵AE=BC，CP=AE,∴BC=PC,∴∠CBP=∠P.∴∠ACB=2∠P,∴∠ACB=2∠AFD.

方法三(图4)

分析D为线段AB的中点，F为线段EC的中点，但DF不是这个图形中三角形的中位线.我们可以尝试再取一个中点，从而构成两条中位线.

证明连接BE，取BE的中点P，连接DP、FP.

∵F为EC的中点,

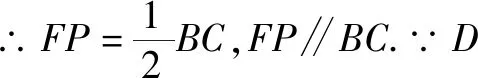
二、倍长线段

方法一(图5)

分析尝试连接线段BF，BF为△ABC的中线，可以联想到倍长中线.

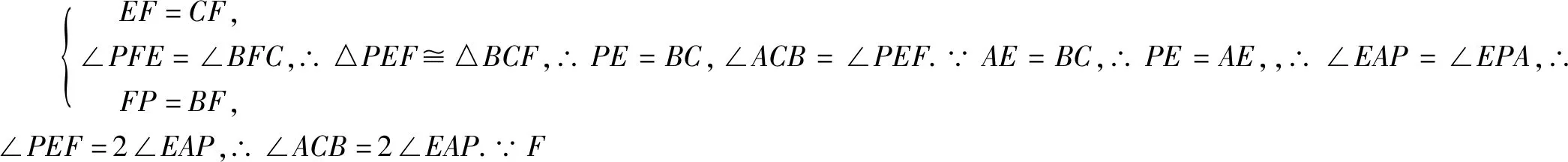
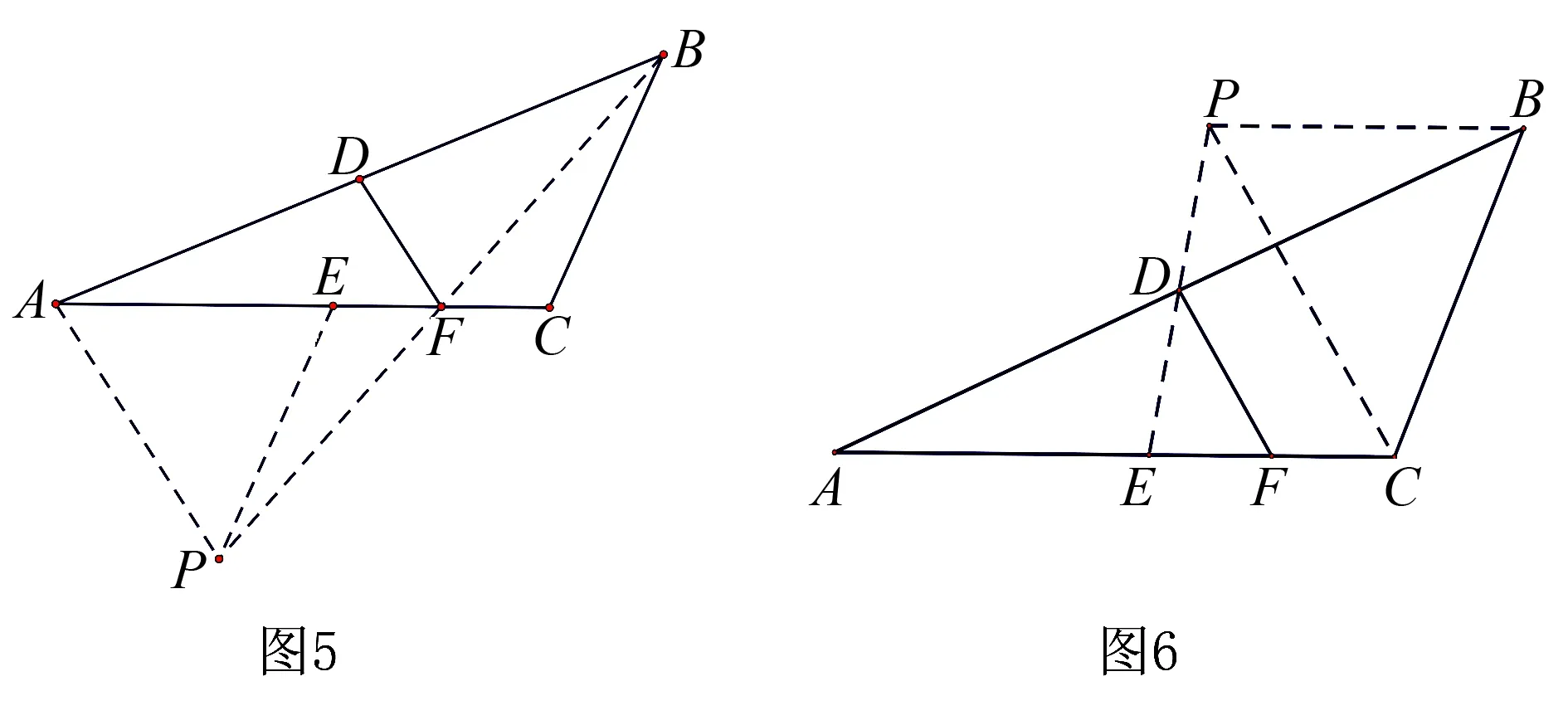
方法二(图6)

分析尝试连接线段ED，D为AB的中点，可以联想到倍长线段ED.

证明连接ED并延长到点P，使得DP=ED，连接BP、CP.

∵F为EC的中点,∴DF∥CP,∴∠AFD=∠ACP.

∵AE=BC,∴BP=BC,∴∠BPC=∠BCP.

∵∠A=∠ABP,∴AC∥BP,∴∠BPC=∠ACP,

∴∠BCP=∠ACP,∴∠ACB=2∠AFD.

方法三(图7)

分析D为AB的中点，尝试倍长线段FD，证明方法类似方法二.

从这个含有中点的典型例题中我们可以看出：由中点联想到作三角形的中位线或倍长线段等方法添加辅助线，通过探索即可找到解决问题的方法和途径.遇到与中点有关的问题时联想到中位线与倍长线段，大胆尝试小心求证即可.