行波效应下劲性骨架混凝土拱桥地震响应规律分析

龚婉婷 杨华平 黎璟 钱永久

（1.西南交通大学土木工程学院，成都 610031；2.四川省交通勘察设计研究院有限公司，成都 610017）

地震时地震波的振幅、相位以及频谱特性随时间和空间的变化而变化，地震多点激励主要体现为部分相干效应、行波效应和局部场地效应［1］。大跨径桥梁结构受地震动空间变异性的影响较为明显，因而在此类结构抗震设计中有必要进行非一致激励分析以考虑空间变异性的影响。研究表明，行波效应对桥梁结构地震响应的影响起主导作用［2］，因此通常采用行波法研究非一致激励对结构的作用。其基本思路是假定场地条件不变，地震波以恒定速度传播，经过各支承点时波形保持不变，分析相位差Δt对结构的影响。

拱桥结构造型优美，施工相对方便，近年来不少学者对拱桥结构受行波效应的影响进行了研究。王君杰等［3］研究了地震动空间变化对大跨度拱桥结构动力特性的影响，认为地震动空间变化对主拱圈内力响应有重要影响。徐燕等［4］选取了存在速度差异的近断层地震波对大跨度钢拱桥进行行波效应分析，得出行波效应对钢拱桥的不同构件有复杂影响。吴玉华等［5］对钢管混凝土拱桥进行了三维正交地震动多点激励下的平稳随机响应分析，发现行波效应能够显著增加拱肋的内力，三维地震作用相较一维地震作用能使拱肋产生更大的内力。王浩等［6］分析了湖南益阳茅草街大桥拱上关键截面响应在行波作用下的变化规律，发现行波效应的影响与结构特性和地震波特性密切相关。楼梦麟等［7］讨论了某大跨公路拱桥在竖向地震动行波输入和一致输入下的动力反应，发现行波地震反应并不随波速单调变化，结构在行波输入下产生较大的地震反应，并提出了行波共振的概念。杨华平等［8］对怒江特大桥进行了非一致地震激励时程分析，发现行波地震响应与波速不存在单调变化关系，为保证设计结果可靠性应选取多种剪切波速计算行波效应对结构的影响。李小珍等［9］采用大质量法对刚构-连续组合桥梁进行了相位差条件下结构非线性地震响应分析，发现在进行行波分析时必须根据基岩类型选择合适的相位输入；在纵向行波作用下，结构内力响应峰值和位移响应峰值随相位差呈周期性变化。

目前，对不同类型的拱桥在行波效应下的地震反应分析还不够全面。因此，本文以主跨445 m 的上承式钢筋混凝土拱桥为研究对象，采用大质量法分析不同相位差下结构的地震响应规律，研究结构峰值响应和相位差之间的关系，以期为大跨度铁路劲性骨架混凝土拱桥抗震设计和相关研究提供科学依据。

1 工程概况与计算模型

1.1 大质量法

大质量法是一种在支承节点上增加附加质量矩阵的方法。附加质量M0通常为结构总质量的106～109倍，且支承处的惯性力视为外力，其动力平衡方程为

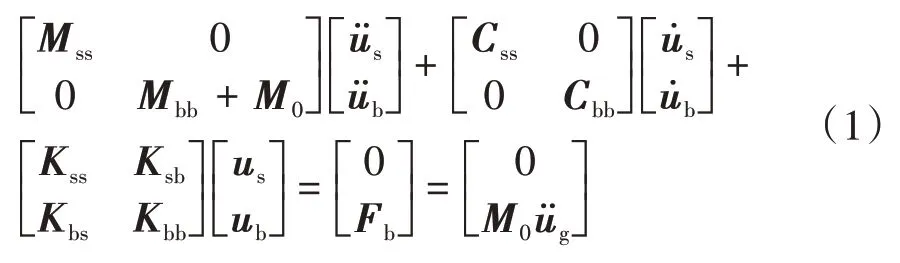
将式（1）第2行展开可得

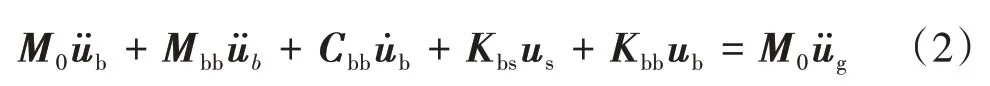
在式（2）中，当大质量M0≫Mbb时远大于等式中其他项，则即支承处的节点加速度与输入的地面加速度一致。由此实现绝对加速度的输入，完成结构动力响应分析。

本文研究对象为大跨度劲性骨架混凝土拱桥，全桥质量为1.3×108kg，在各墩底添加附加质量1×1015kg，并释放与地面支承处纵桥向的约束，同时在该方向上施加时程力即可构建大质量法有限元模型。由于大质量法计算结果为绝对响应，无法区分拟静力响应与动力响应，所以计算过程中存在一定程度的等效。

1.2 桥梁概况

某客运双线高速铁路大桥全长721.2 m，线间距5 m，主桥为445 m 上承式劲性骨架混凝土拱桥，设计速度为300 km/h。受温度及徐变作用影响，桥面竖向变形较大，为确保轨道平顺性，该桥轨道结构设计采用聚氨酯固化道床。主桥拱圈采用C60 混凝土，上部结构采用C55 混凝土。拱圈拱轴线采用悬链线，矢高100 m，矢跨比1/4.45。拱圈为单箱三室、等高变宽箱形截面，拱圈高度9 m。上部结构孔跨布置为32.75 m预应力混凝土简支梁+2×65.9 m 预应力混凝土T 构+4×62 m 预应力混凝土连续梁+主 4×62 m 预应力混凝土连续梁+2×65.9 m 预应力混凝土 T 构+2×32.85 m 预应力混凝土简支梁。桥型总体布置见图1。

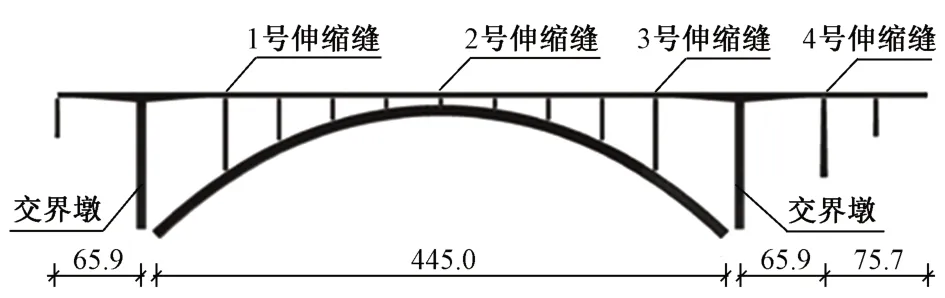
图1 桥型总体布置（单位：m）

1.3 结构有限元模型

采用SAP2000 建立了基于大质量法的动力分析模型（图2），变截面箱梁、拱圈、拱上立柱以及桥墩均采用空间梁单元，拱脚、引桥桥墩与地面固结。模型共建立了690 个空间梁单元，采用弹性连接单元模拟桥面伸缩缝。结构质量考虑了结构自重和二期荷载，其中竖向自重加速度为9.806 m/s2，二期恒载采用单元线荷载形式施加，大小为160 kN/m。采用瑞利阻尼进行地震响应分析，即C=αM+βk（α和β 均为瑞利系数），选取质量参与系数大的振型频率来进行结构地震响应分析［10］，设阻尼比为0.05，计算得到α=0.099 7，β=0.024 6。

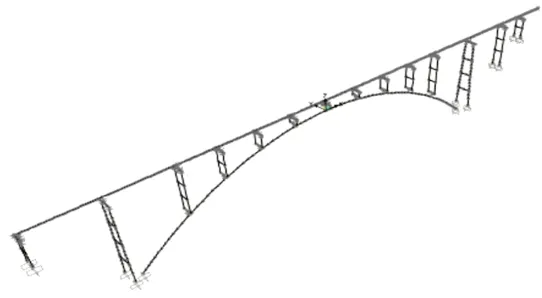
图2 动力分析模型

采用子空间迭代法进行结构动力特性分析，前10阶振动特性见表1。

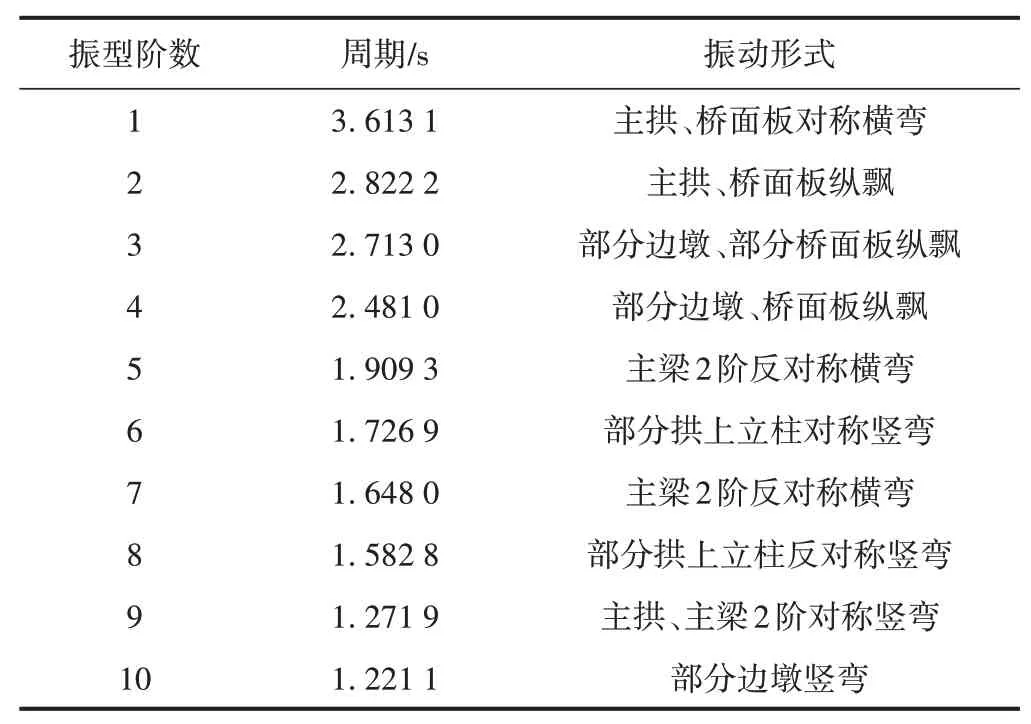
表1 前10阶振动特性

1.4 地震波选取

在进行结构时程分析计算时，选用合适的地震波十分重要，应尽可能选取震级、震中距和土壤性质、卓越周期等条件相近的地震记录作为地震波输入的基本频谱。为便于对比分析，还应该选取多条具有该场地特征代表性的地震波进行时程分析。基于以上考虑，从NGA-West2数据库中选取了地表30 m土层平均剪切波速VS30，以及矩震级、峰值加速度均比较接近的4 条地震波用于时程分析，通过调整调幅系数将各波加速度峰值统一为0.2g。地震波采取沿桥梁纵向从左向右的输入方式。选取波的地震动特性见表2，调幅后加速度时程曲线见图3。

表2 地震动特性

图3 地震记录加速度时程曲线

2 结构在行波效应下响应规律分析

地震作用下结构的动力响应主要是由自身动力特性和外部激励决定，而结构在行波效应下的动力响应主要来自相位差造成的拟静力项以及正反对称振型的贡献［11］。结构的1 阶纵向自振周期T约为2.9 s，以0.1T为时间间隔计算了0.1T～2.9T桥梁纵向非一致激励下的动力响应。

2.1 伸缩缝位移分析

为研究不同相位差下结构的地震响应的规律，对纵向非一致激励与一致激励计算结果的比值进行了分析，结果见图4。图中，u和u0分别为不同相位差非一致激励和一致激励下拱桥的伸缩缝位移。

由图4可知：①1号，3号和4号伸缩缝位移响应峰值均随Δt呈明显周期性变化，且3 号，4 号伸缩缝的位移响应相比1 号规律更加明显；②3 号，4 号伸缩缝的位移变化与结构1阶纵向自振周期相似；③2号伸缩缝位移响应并没有显示出明显的周期变化，在非一致激励下的响应比一致激励时大50～150 倍。表明与一致激励相比，非一致激励下对称结构在结构中部的位移响应会显著增加。

图4 不同各相位差下伸缩缝位移响应峰值

对3 号和4 号伸缩缝进一步分析可知，当Δt为0.5T，1.5T，2.5T时，各波作用下伸缩缝的位移响应处于谷值；当Δt为1T和2T时，各波伸缩缝的位移响应处于峰值。说明在非一致激励下，相位差为结构自振周期（2n+1）/2 倍（n为整数）时，桥梁伸缩缝位移始终处于位移响应的谷值，桥梁位移响应值会在一定程度上有所降低。因此对劲性骨架混凝土拱桥进行抗震设计时，需调整桥梁拱脚间距及结构1阶纵向自振周期，使得地震响应到达主拱之间的时差尽量接近结构1阶纵向自振周期的（2n+1）/2 倍，以减轻行波效应下的结构位移响应。

2.2 拱圈关键部位内力分析

2.2.1 弯矩

不同相位差非一致激励下，拱脚、L/4 拱和拱顶弯矩响应峰值M与一致激励下弯矩响应峰值M0的比值见图5。

由图5 可知，拱顶弯矩的变化规律同跨中伸缩缝的位移变化规律相似。在结构抗震设计中，应控制结构相位差接近结构1 阶纵向自振周期的（2n+1）/2 倍，可有效降低结构内力响应。

2.2.2 轴力

不同相位差非一致激励下，拱脚、L/4 拱和拱顶轴力响应峰值P与一致激励下弯矩响应峰值P0的比值见图6。

由图6 可知，拱脚、L/4 拱的轴力并不像弯矩一样随着相位差的改变而发生周期性变化，其轴力在行波效应下表现为先增大、后减小，最后趋于一相对稳定的范围。拱顶的轴力变化最大，其值为一致激励下拱顶轴力的100～300 倍，同拱顶弯矩以及跨中伸缩缝位移变化规律相符。

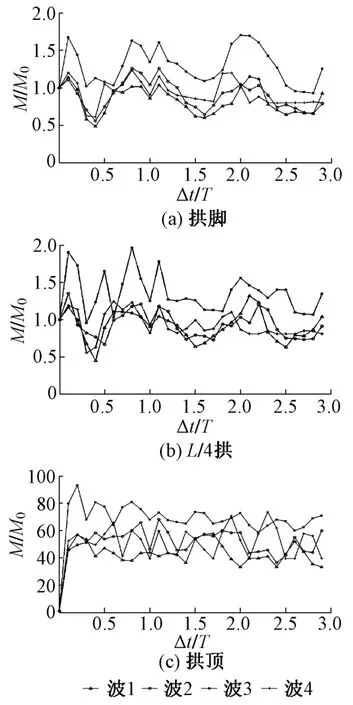
图5 不同相位差下拱圈关键截面弯矩响应峰值

图6 不同相位差下拱圈关键截面轴力响应峰值

3 结论

1）非一致激励下，伸缩缝位移响应峰值（除跨中）与拱脚和L/4 拱圈处弯矩响应峰值均随相位差呈周期性变化，且表现出与结构一阶纵向周期T一致的周期特性：在Δt=（2n+1）T/2 时结构动力响应处于谷值，在Δt=2n时结构动力响应处于峰值。

2）拱脚和L/4 拱圈的轴力表现为先增大、再减小，最后在某一范围浮动，且大于在一致激励下的值。

3）在行波效应下，结构部分构件动力响应与相位差存在相关性，对相位差与结构自振周期的比值进行控制能有效改善结构动力响应。

4）拱桥跨中伸缩缝位移和拱顶轴力与相位差无明显相关性。行波效应极大增强了对称结构在结构中部的地震响应，其值比一致激励下的结构响应分别增大50～150倍，100～300倍。

5）非一致激励会增大结构的地震响应，在对大跨度桥梁进行抗震设计时不可忽略行波效应的影响。

本文只分析了一种类型的拱桥在不同相位差下的地震响应，尚未考虑基础和土的相互作用以及结构非线性等因素，有必要对此类桥型做进一步研究。