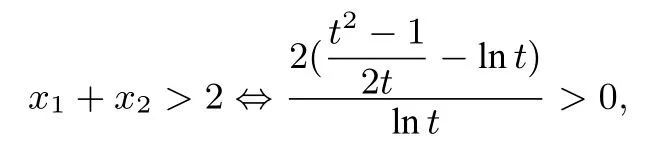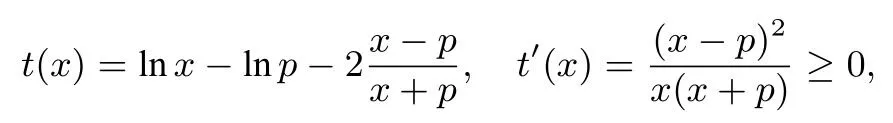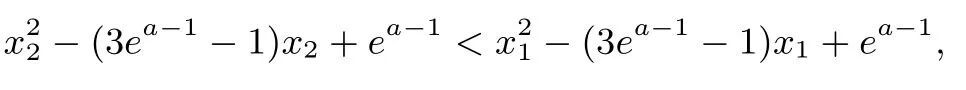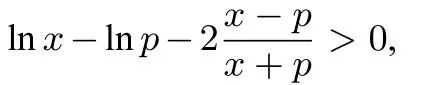一般与特殊:极值点偏移难题的解法探究
广东省广州市华南师范大学附属中学
极值点偏移问题是近年来高考题与模拟题中的热点问题,研究这类问题的文章汗牛充栋[1-2],但是本文拟就一些难题谈一谈本人的一些心得体会.通常来说我们有三种处理方法:构造函数法,换元法与对数均值不等式法.下面,以一道常见的题为例.
题目已知函数f(x)=lnx-ax有两个相异零点x1,x2,求证:x1x2>e2.
(1)构造函数法因为观察到的极值点刚好为e,构造利用h(e)=0,再考虑h(x)的导数从而证明结论.
(2)换元法令x2=tx1(t>1),代入得故实现了二元变一元.
(3)对数均值不等式法利用常用的对数均值不等式[3]:其中x1,x2为不相等的正数.本题中,lnx1=ax1,lnx2=ax2,
但是,实际在解题过程中,相信广大师生会发现有三种主要的困难:
(1)有些题目所要证的并非x1+x2,x1x2大于或小于某个定值的结论,即不是一个常规的极值点偏移问题,使得我们产生这道题应不应该用极值点偏移的方法来做的困惑.
(2)有些题目里面含参变量有三个:x1,x2,a,难以化成一元的函数或不等式来证明.
(3)有些题目并不是这三种方法都可行,可能只有一两种方法是可行的,有时甚至要运用一些其他的方法.
下面我们分别以一些例子来说明.
例1设F(x)= 2 lnx-x2-kx有两个零点m,n(0< m < n),且m+n=2x0,问函数F(x)在x0点处的切线能否平行于x轴?
证明(代数变形+对数均值不等式法)
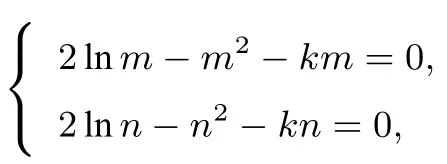
由题意得两式相减得

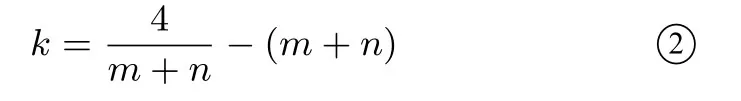
评注本题若用构造函数法和换元法,一般来说是无效的,因为这是一个开放性的问题,它不属于常规的极值点偏移问题.
例2F(x)=x-lnx-a有两个零点x1,x2.求证:
尝试1 (构造函数法)因为本题中的极值点为x=1,F(1)=1-a.
由题意知a >1,x1<1< x2,所以x1+x2> a+1⇔x2>a+1-x1⇔F(x2)>F(a+1-x1).
构造函数g(x)=F(x)-F(1+a-x),则只需证g(x)>0,x ∈(1,+∞),
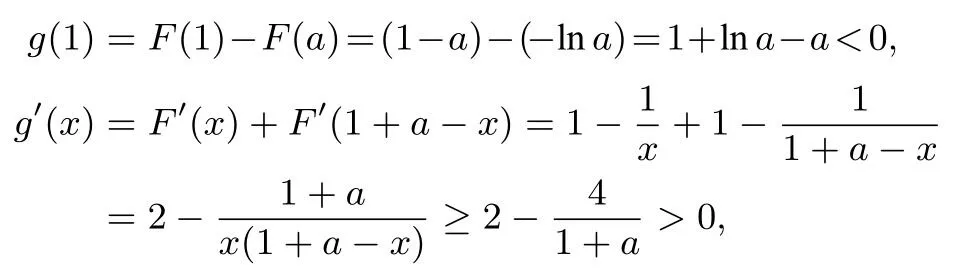
所以g(x)≥g(1)<0! 并不能证明我们心目中所想的不等号方向,证明失败了!
尝试2 (代数变形+对数均值不等式法)
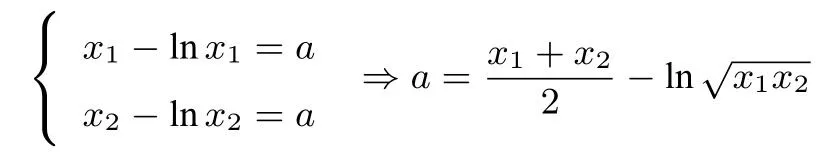
两式相减得x1-x2=lnx1-lnx2,由对数均值不等式知
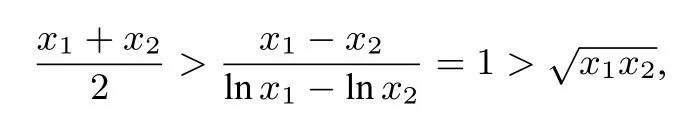
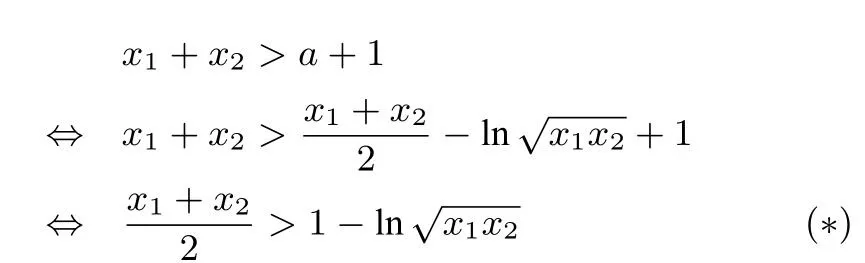
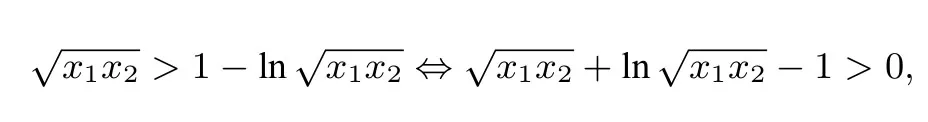
尝试3 (换元法)
由于x1-lnx1=x2-lnx2=a,原不等式⇔x1+x2>x1-lnx1+1⇔x2+lnx1>1.
进行换元法,令x2=tx1,(t >1)代入得x1-lnx1=tx1-ln(tx1),所以所以原不等式等价于
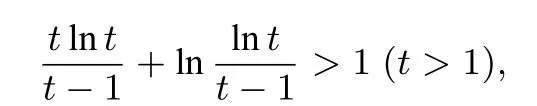
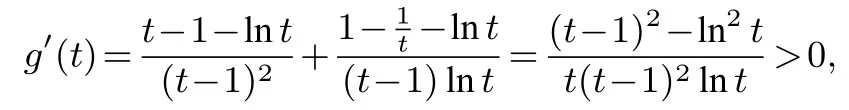
评注本题中F(x)的极值点并不是是两个零点,所以严格的来说,这并不是一道极值点偏移问题,而可以称为零点偏移问题.我们历经了两种失败的方法,才终于找到一种可行的方法—-换元法,而且计算量也比较大,涉及到了对复合函数的求导,比通常的换元法困难很多.
例3已知函数f(x)=a--lnx(a ∈R),若函数有两个零点x1,x2(x1 证明(1)先证x1+x2>2,由题意得,所以 (2)再证x1+x2<3ea-1-1.因为f(x)=0⇔h(x)=ax-1-xlnx=0,故x1,x2也是h(x)的两个零点,由h′(x)=a-1-lnx=0 得x=ea-1(记ea-1为p),易知p是h(x)的唯一最大值点,故有h(p)>0,x1 故h(x)单增.当x>p时,t(x)>t(p)=0,当0 即(x2+x1)(x2-x1)<(3ea-1-1)(x2-x1),于是x1+x2<3ea-1-1. 综上所述,2 评析1 本题中的左端不等式易证,常规的三种方法都可以做出. 2 本题中不等式的右端比较难证,而关键之处又是难以想到题目中所给出辅助函数而实际上,当我们把对数均值不等式中的x1变为x,x2变为p,不难得到这正是我们所构造的函数! 归根结底,这道题的本质还是利用对数均值不等式对lnx进行放缩,从而得到了右端这个看起来令人望而生畏的不等式. 结语以上三道例题分别对应了我们常见的三种困难,从上述分析可知,如果要攻破极值点偏移问题中的难题,尤其是含参的问题,不仅需要我们掌握三种常规的方法,还需要慧眼识珠,认清题目属不属于我们处理过的种类,如果属于极值点偏移问题,我们应该采取哪种策略比较可行,更需要灵活变通,在一种方法行不通的情况,能够尝试使用其他的方法. 最后,我们提供几道练习,供各位读者使用. 练习 1.(2019 届武汉市四月调研测试)已知函数f(x)=(a为常数),在区间(0,2)内有两个极值点x1,x2(x1 (1)求实数a的取值范围; (2)求证:x1+x2<2(1+lna). (1)讨论f(x)的单调性; (2)若f(x)=b存在两个不等的实数根x1,x2,求证: 3.已知函数f(x)=x2+ln(x+a). (1)讨论f(x)的单调性; (2)若f(x)存在两个极值点x1,x2,求证: 无论实数a为何值都有