光学舱外形对子弹转速的影响数值研究*

刘文举，赵养正，梁建峰，雷永信

(西安现代控制技术研究所，西安 710065)

0 引 言

末敏弹是典型的智能弹药，通常为子母式结构，当子弹从母弹弹体抛出后，减速伞张开减速，子弹光学舱旋出，子弹体成为几何非对称结构，从而产生旋转运动，这一转速的大小和方向直接影响后序主旋转伞的开伞性能。目前对旋转弹箭的气动特性的研究较多，文献[1-2]分别用实验和数值的方法对平头圆柱体+四片翼子弹的滚转阻尼进行了研究，文献[3-5]数值研究了导弹旋转状态下的动导数，文献[6]研究了在旋转状态下一种异形卷弧翼弹的气动特性，但研究这种光学舱几何变化对子弹转速的影响，还未有公开的文献，因此通过数值方法研究光学舱不同几何形状对子弹转速的影响规律对解决主旋转伞可靠开伞意义重大。

1 模型

模型结构为台阶型弹体+旋开式光学舱(见图1)。此气动外形弹体完全相同，光学舱的几何外形有外弧面+内平面+左凸台、外平面+内平面+左凸台、外弧面+内弧面+左凸台、外弧面+内平面+无凸台、外弧面+内弧面+宽凸台等形式。

2 数值方法

2.1 计算方法

文中使用cfx 软件进行数值计算。具体计算方法为: 结合SST 湍流模型，并采用有限体积中心差分格式对三维雷诺平均Navier-Stokes 方程进行求解。在计算滚转阻尼时，采用了和文献[1]相同的方法，坐标系固定在子弹体上，随子弹一起以固定的角速度旋转。入口边界采用速度和温度；出口边界采用静压和温度；远场边界采用无粘滑移边界墙；壁面边界采用无滑移壁面条件。

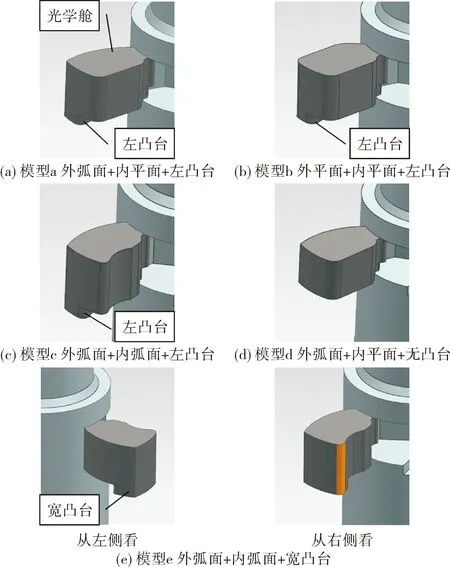
图1 光学舱外形示意图

转速计算公式：

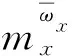
2.2 计算网格

外场采用四面体网格，附面层采用三棱柱形网格。模型的表面网格和附面层网格见图2和图3。

图2 表面网格

2.3 计算条件

1)静态计算条件

速度：40 m/s、65 m/s、200 m/s；攻角：-7°、-2°、 3°。

2)准静态计算条件

速度：40 m/s、65 m/s、200 m/s；攻角：-7°、-2°、 3°；

转速：0～5 r/s。

图3 附面层网格和外场网格

3 结果与讨论

对静态和旋转状态的气动滚转力矩和阻尼力矩进行了计算，通过转速计算公式，获得不同光学舱子弹的转速，并对计算结果进行了比较分析。

3.1 转速结果分析

规定沿弹轴从弹尾向弹头看顺时针旋转为负转速，逆时针旋转为正转速，由图4负攻角7°时的转速曲线可以看出：光学舱有左凸台的a、b、c三种模型转速较高，而且随速度增加，转速逐渐增大；无凸台的d模型和宽凸台的e模型转速较低，转速在2 r/s以内，转速的变化也较小。图5负攻角2°时的转速曲线和图6正攻角3度时的转速曲线也有类似的情况。因此在设计光学舱的几何外形时，应考虑外形对子弹转速的影响，避免转速较高引起的开伞缠伞现象的发生，提高开伞成功率。

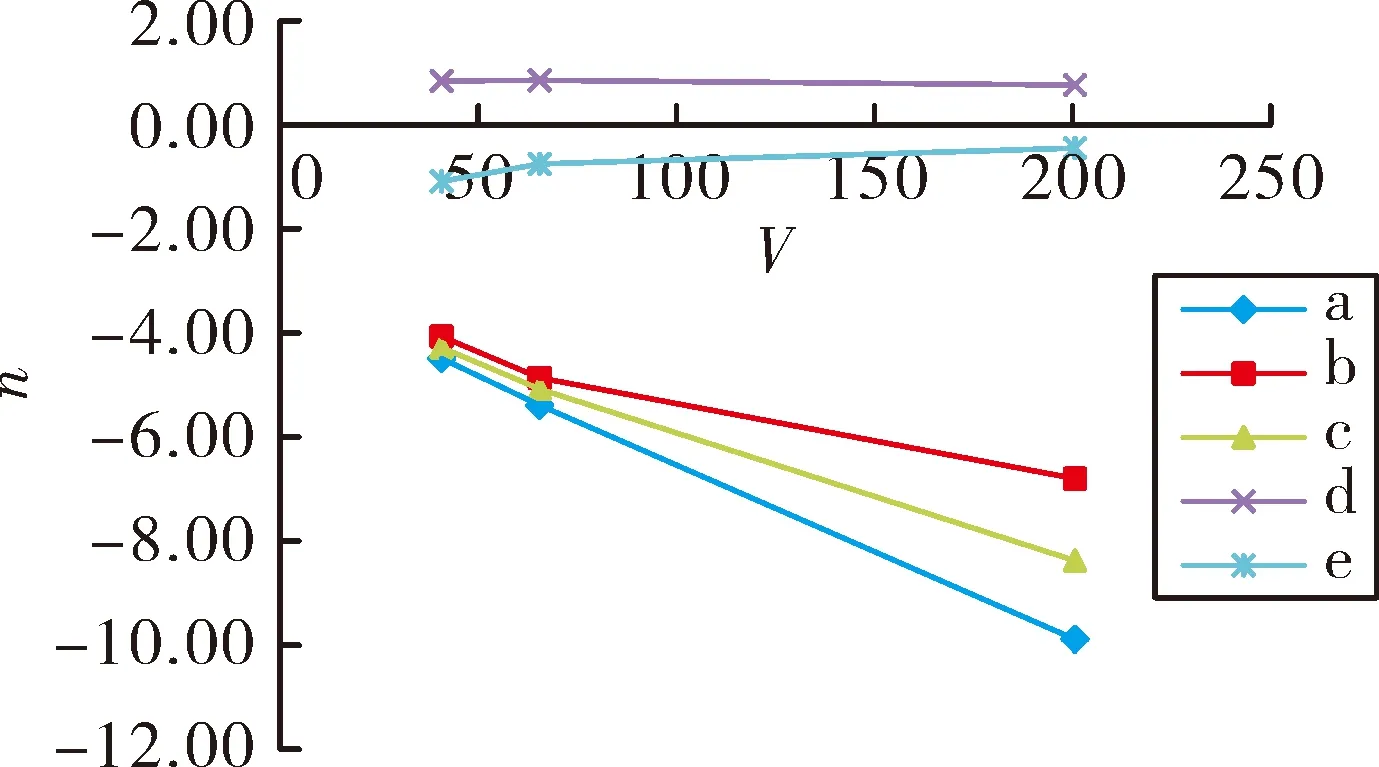
图4 不同光学舱子弹的转速随速度的变化曲线(α=-7°)

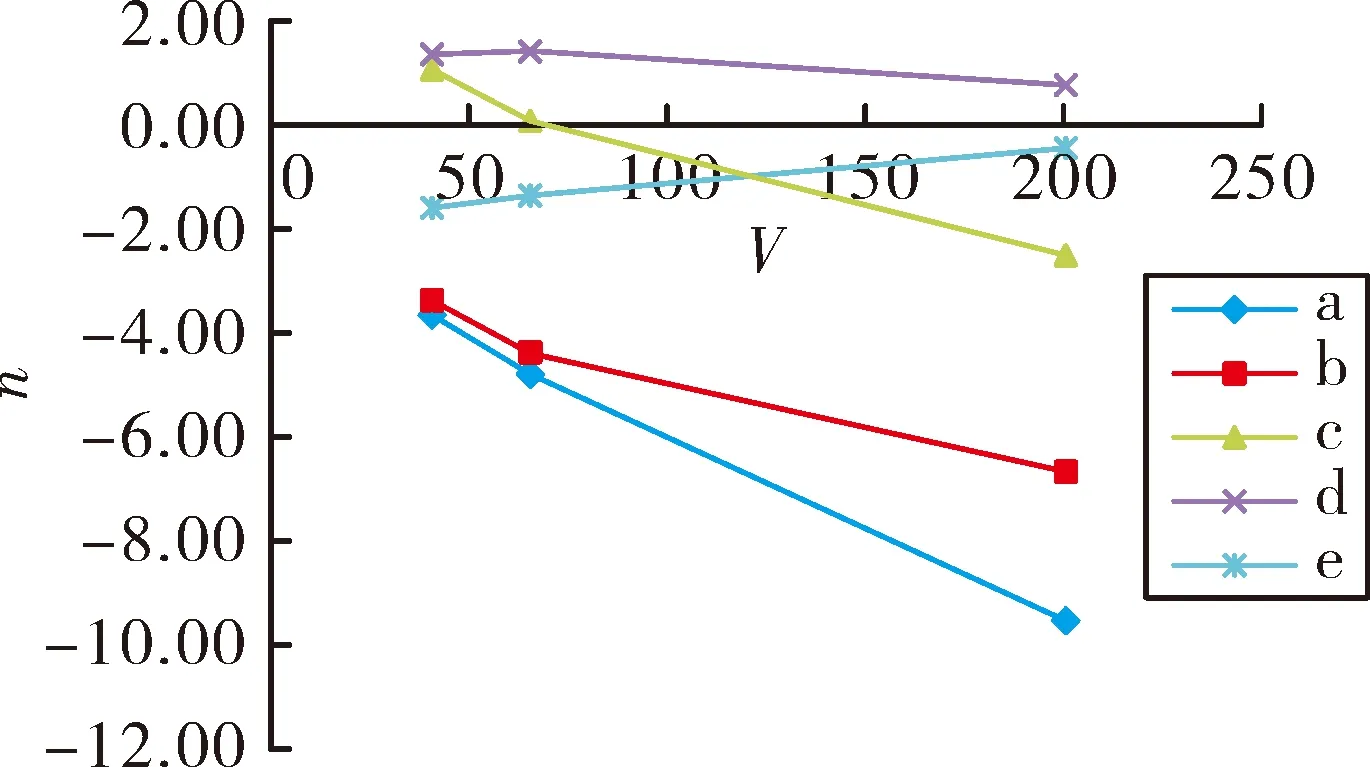
图5 不同光学舱子弹的转速随速度的变化曲线(α=-2°)

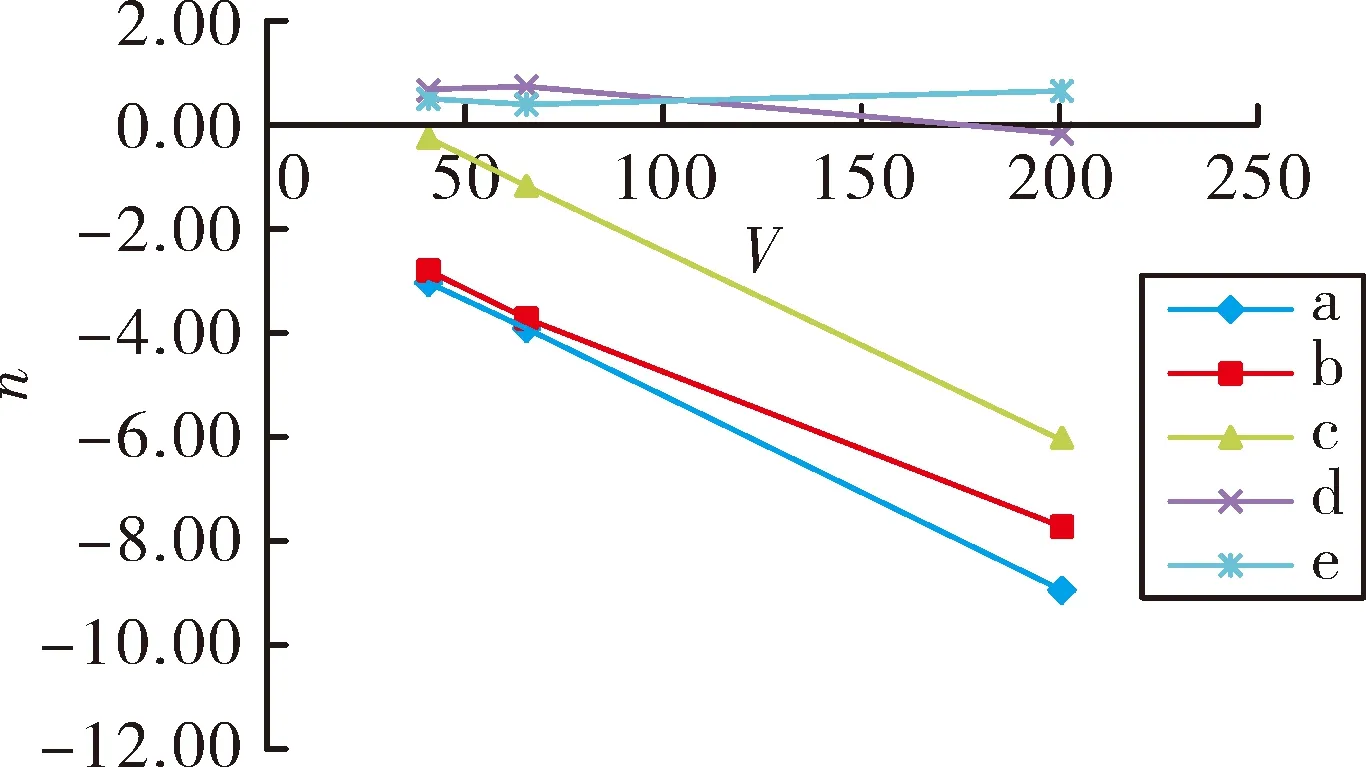
图6 不同光学舱子弹的转速随速度的变化曲线(α=3°)

3.2 流场分析

从第3.1节转速结果分析可以看出光学舱的几何形状对子弹转速有较大影响，下面从流场的角度对这种影响做进一步研究。从图7光学舱部位的压力云图可以看出，光学舱左凸台内侧，压力较大，而光学舱外圆弧面的压力较小，因此形成了压力差，光学舱受到由内平面向外弧面的力，这样，沿弹轴从弹尾向弹头看，弹体将顺时针旋转。从图8无凸台光学舱部位的压力云图可以看出，光学舱外弧面和内平面的压力几乎相同，压力差较小，弧面的压力稍大于内平面，因此光学舱受到由外弧面向内平面的力，这样，沿弹轴从弹尾向弹头看，弹体将逆时针旋转。从这两种外形的压力云图对比分析，可以进一步说明光学舱左凸台对顺时针转速有较大影响，在光学舱结构设计时应充分考虑凸台的高度不能太高，否则顺时针转速会增大。

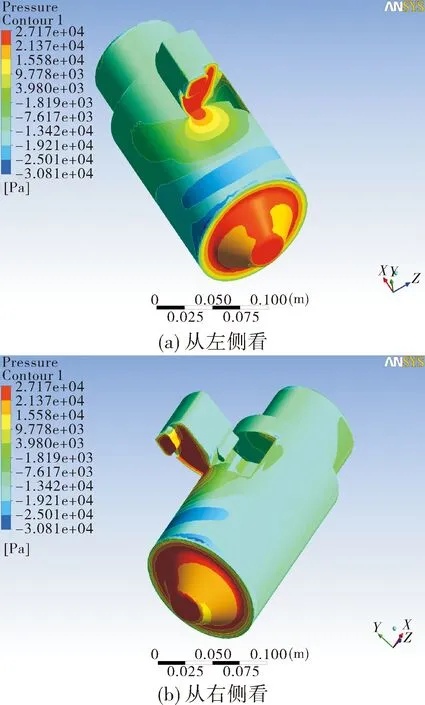
图7 速度200 m/s时左凸台模型a的压力云图(α=7°)

图8 速度200 m/s时无凸台模型d的压力云图(α=7°)

图9 速度200 m/s时有左凸台模型b和c的压力云图(α=7°)

从图1中模型b和c的外形比较来看，模型b内外面均为平面形，而模型c内外面均为圆弧形，二者均有左凸台，从图9的流场可以看出，双弧面内面的压力比双平面的内面压力稍小，而左凸台对压力影响远大于内外面的压差影响，因此从图4中的转速曲线也可以看出，模型b和模型c的转速均较大，这种情况也和有左凸台的模型a的转速曲线接近。从图10宽凸台模型e的压力云图可以看出，内外面、宽凸台两侧的压力差较小，与左凸台模型c相比，从左凸台改为宽凸台降低了凸台处的压力差，因此从图4、图5、图6都可以看出，宽凸台模型e的转速减小。

图10 速度200 m/s时宽凸台模型e的压力云图(α=7°)

3.3 试验验证

试验是在CG-02低速直流开口立式风洞(稳态扫描环境模拟试验装置)中进行模拟的，试验段见图11。该风洞收缩段出口直径为Φ4.5 m，试验段射流长度为6.5 m，试验段风速范围5～50.8 m/s。 本次验证试验采用文献[7]的试验方法。

图11 开口式立式风洞试验段

图12展示了模型a在试验段试验的状态，T1、T2、T3和T4代表了旋转的时间顺序，可以看出模型沿弹轴从弹尾向弹头看顺时针旋转。

图13为风速40 m/s时的瞬时转速测量结果，可以看出转速随时间波动式变化，平均值为3.36 r/s。

图12 风速为40 m/s时，按旋转的时间顺序展示的瞬时图片

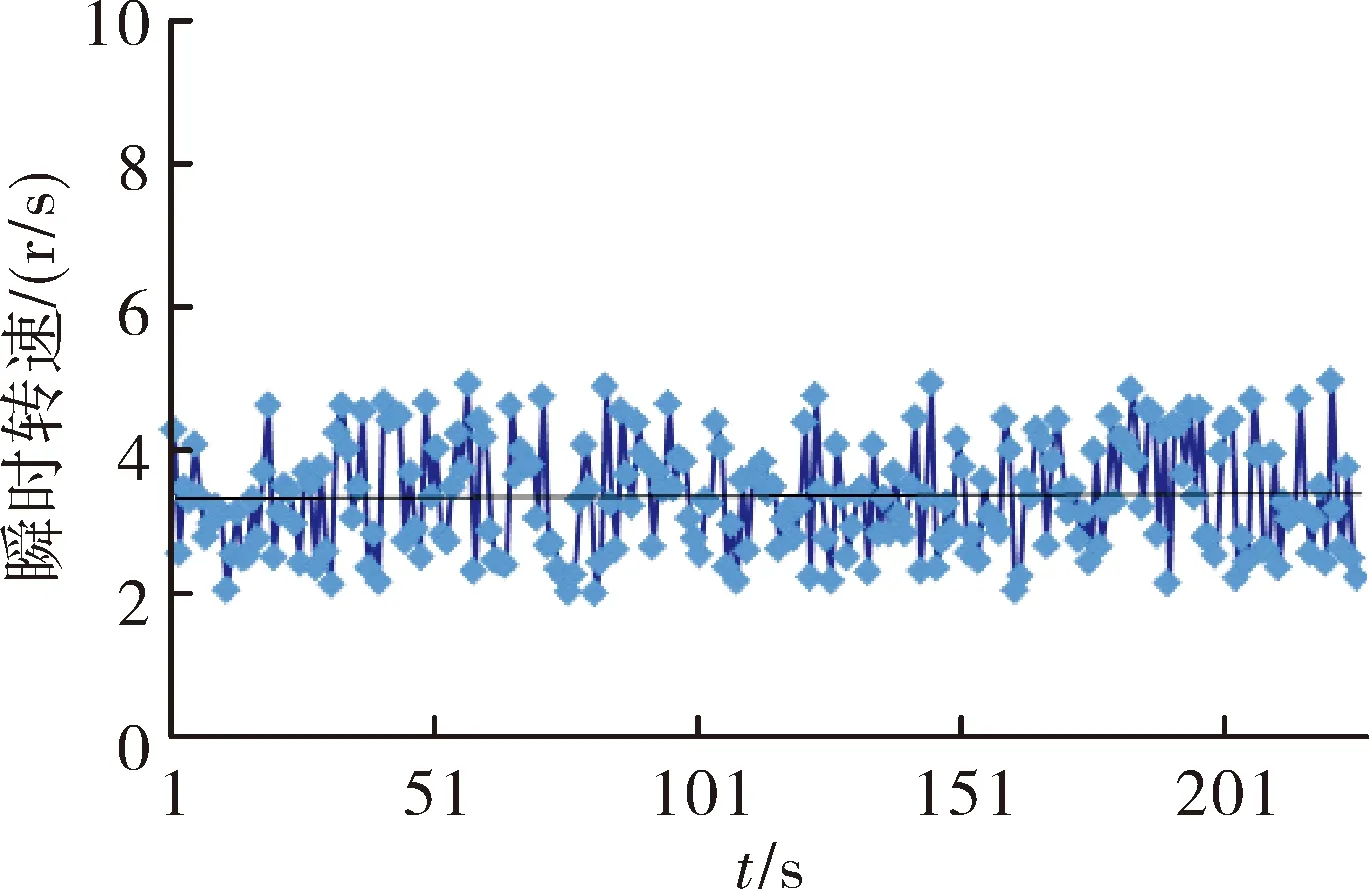
图13 风速为40 m/s时，瞬时转速随时间的变化曲线

表1为不同风速下平均转速的测量值，虽然风速不同，但平均转速较为接近，因此在设计转速时，可以认为5 m/s以内的风速差距对转速的影响非常小。

表1 不同风速时平均转速的测量结果

从表1中状态2的测量值3.36 r/s，与图5中模型a，风速为40 m/s的数值计算转速3.65 r/s的对比可以看出，二者数值非常接近，而且转速方向相同，只是数值计算结果稍大，因此，数值计算转速的方法具有较好的工程应用价值。

4 结论

通过数值计算的方法研究了光学舱几何结构变化对子弹转速大小及方向的影响，并通过流场分析和与实测转速结果的对比得出结论：

1)采用文中的数值方法计算的转速实用、可靠，与试验结果一致性好；

2)光学舱的几何形状影响子弹的转速及旋转方向；

3)在设计光学舱结构时，应注意迎风端左凸台高度的增加，会引起子弹的顺时针转速增大；

4)当光学舱采用宽凸台结构时，可以减小子弹的转速；

5)当光学舱迎风端无凸台时，会产生较小的转速。